ค่าเฉลี่ยฮาร์มอนิก
ที่นี่เราจะอธิบายว่าค่าเฉลี่ยฮาร์มอนิกคืออะไรและคำนวณอย่างไร (สูตร) นอกจากนี้เรายังคำนวณค่าเฉลี่ยฮาร์มอนิกของตัวอย่างทีละขั้นตอน คุณยังจะพบเครื่องคิดเลขที่ใช้หาค่าเฉลี่ยฮาร์มอนิกของชุดข้อมูลใดๆ ด้วย และสุดท้าย คุณจะสามารถดูได้ว่าคุณสมบัติของค่าเฉลี่ยฮาร์มอนิกคืออะไร
ค่าเฉลี่ยฮาร์มอนิกคืออะไร?
ค่าเฉลี่ยฮาร์มอนิกคือการวัดตำแหน่งศูนย์กลางของสถิติเชิงพรรณนา ค่าเฉลี่ยฮาร์มอนิกคำนวณโดยการหารจำนวนข้อมูลทางสถิติทั้งหมดด้วยผลรวมของส่วนกลับของแต่ละค่า
ค่าเฉลี่ยฮาร์มอนิกใช้ในการคำนวณความเร็วเฉลี่ย เวลา หรือทำการคำนวณทางอิเล็กทรอนิกส์ คุณลักษณะนี้ทำให้ค่าเฉลี่ยฮาร์มอนิกแตกต่างจากค่าเฉลี่ยประเภทอื่นๆ ซึ่งมักใช้ในการคำนวณราคาหรือเปอร์เซ็นต์เฉลี่ย
ดังนั้น สูตรหาค่าเฉลี่ยฮาร์มอนิกจึงเป็นดังนี้:

ค่าเฉลี่ยฮาร์มอนิกมักจะแสดงด้วยตัวพิมพ์ใหญ่ H
ค่าเฉลี่ยประเภทอื่นๆ ที่มีอยู่ ได้แก่ ค่าเฉลี่ยเลขคณิต ค่าเฉลี่ยถ่วงน้ำหนัก ค่าเฉลี่ยกำลังสอง และค่าเฉลี่ยเรขาคณิต ค่าเฉลี่ยฮาร์มอนิกมีข้อดีและข้อเสียเมื่อเปรียบเทียบกับค่าเฉลี่ยประเภทอื่นๆ ด้านล่างเราจะดูว่ามีอะไรบ้าง
วิธีการคำนวณค่าเฉลี่ยฮาร์มอนิก
ในการคำนวณค่าเฉลี่ยฮาร์มอนิก จะต้องดำเนินการตามขั้นตอนต่อไปนี้:
- คำนวณค่าผกผันของข้อมูลทางสถิติแต่ละรายการในกลุ่มตัวอย่าง
- เพิ่มค่าผกผันที่คำนวณได้ทั้งหมด
- หารจำนวนข้อมูลทั้งหมดด้วยผลรวมที่พบในขั้นตอนก่อนหน้า
- ผลลัพธ์ที่ได้คือค่าเฉลี่ยฮาร์มอนิกของตัวอย่างทางสถิติ
👉 อย่างที่คุณเห็น การหาค่าเฉลี่ยฮาร์มอนิกของชุดข้อมูลนั้นต้องใช้การดำเนินการจำนวนมาก ดังนั้นจึงค่อนข้างลำบากหากจะทำด้วยมือ ดังนั้น ในการคำนวณค่าเฉลี่ยฮาร์มอนิก เราขอแนะนำให้ใช้เครื่องคิดเลขด้านล่างนี้
ตัวอย่างของค่าเฉลี่ยฮาร์มอนิก
หลังจากดูทฤษฎีเกี่ยวกับค่าเฉลี่ยฮาร์มอนิกแล้ว เราจะมาดูวิธีค้นหาค่าเฉลี่ยฮาร์มอนิกของชุดข้อมูลโดยการแก้ตัวอย่างราคาหุ้นทีละขั้นตอน
- บุคคลซื้อหุ้นของบริษัททุกปีเป็นเวลา 5 ปีติดต่อกัน ในช่วงเวลานี้ ราคาของหุ้นมีความผันผวนอย่างมาก: ในปีแรกแต่ละหุ้นมีมูลค่า €7 ในปีที่สอง €10 ในปีที่สาม €15 ในปีที่สี่ บริษัทประสบกับความสูญเสียทางการเงินที่สำคัญ และ ราคาลดลงเหลือ 6 ยูโรต่อหุ้น และในที่สุดในปีที่ 5 บริษัทได้ทำการลงทุนจำนวนมากจนทำให้ราคาสูงขึ้นเป็น 11 ยูโร ราคาซื้อหุ้นเฉลี่ยอยู่ที่เท่าไร?
ทางเลือกหนึ่งคือการคำนวณค่าเฉลี่ยเลขคณิต นั่นคือ บวกราคาทั้งหมดแล้วหารด้วย 5 อย่างไรก็ตาม เนื่องจากการซื้อเกิดขึ้นในปีต่างๆ กัน การใช้ค่าเฉลี่ยเลขคณิตจึงถือเป็นข้อผิดพลาด เราจึงต้องหาค่าเฉลี่ยฮาร์โมนิคของราคาทั้งหมด
ต่อไป เราใช้สูตรค่าเฉลี่ยฮาร์มอนิก:
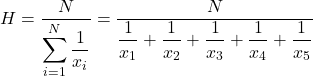
จากนั้นเราจะแทนที่ค่าราคาที่เป็นปัญหาลงในสูตรและคำนวณค่าเฉลี่ยฮาร์มอนิก:
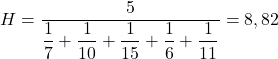
คุณต้องใส่ 5 ในตัวเศษของเศษส่วน เนื่องจากมีข้อมูลที่แตกต่างกัน 5 ส่วน
ดังนั้น ราคาเฉลี่ยของหุ้นที่คุณซื้อในช่วงเวลานี้คือ 8.82 ยูโรต่อหุ้น
เครื่องคำนวณค่าเฉลี่ยฮาร์มอนิก
ด้วยเครื่องคิดเลขต่อไปนี้ คุณสามารถคำนวณค่าเฉลี่ยฮาร์มอนิกของชุดข้อมูลทางสถิติใดๆ ได้
คุณต้องป้อนตัวเลขโดยใช้จุดเป็นตัวคั่นทศนิยม และคั่นตัวเลขด้วยการเว้นวรรค จำไว้ว่าการหาค่าเฉลี่ยฮาร์มอนิก ไม่มีค่าใดที่เป็นศูนย์ได้
คุณสมบัติของค่าเฉลี่ยฮาร์มอนิก
ค่าเฉลี่ยฮาร์มอนิกมีลักษณะดังต่อไปนี้:
- ค่าขนาดใหญ่มีผลเพียงเล็กน้อยต่อค่าเฉลี่ยฮาร์มอนิกของวงดนตรี นั่นคือค่าที่สูงมากเมื่อเทียบกับข้อมูลอื่นจะไม่ทำให้เกิดการเปลี่ยนแปลงที่เห็นได้ชัดเจนในค่าเฉลี่ยฮาร์มอนิก
- ในทางกลับกัน ค่าเล็กน้อยจะมีอิทธิพลอย่างมากต่อค่าเฉลี่ยฮาร์มอนิกของวงดนตรี ส่งผลให้ค่าของมันลดลงอย่างมาก อันที่จริง ส่วนกลับของตัวส่วนของสูตรนั้นจะใช้ค่าที่สูงมาก
- ไม่สามารถคำนวณค่าเฉลี่ยฮาร์มอนิกได้หากข้อมูลใดๆ เป็นศูนย์ เนื่องจากจะทำให้สูตรไม่แน่นอน ในกรณีเช่นนี้ กล่าวได้ว่าค่าเฉลี่ยฮาร์มอนิกไม่ได้กำหนดไว้
- ส่วนกลับของค่าเฉลี่ยฮาร์มอนิกเทียบเท่ากับค่าเฉลี่ยเลขคณิตของส่วนกลับของการสังเกต
- สำหรับข้อมูลกลุ่มเดียวกัน ค่าเฉลี่ยฮาร์มอนิกจะน้อยกว่าหรือเท่ากับค่าเฉลี่ยเลขคณิต
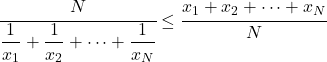
คำนวณค่าเฉลี่ยฮาร์มอนิกด้วย Excel
ดังที่เราได้เห็นมาแล้ว การคำนวณค่าเฉลี่ยฮาร์มอนิกด้วยตนเองอาจค่อนข้างน่าเบื่อ เนื่องจากจำเป็นต้องทำการคำนวณหลายอย่าง และจะยิ่งซับซ้อนยิ่งขึ้นเมื่อคุณมีข้อมูลจำนวนมาก ดังนั้นหากต้องการหาค่าเฉลี่ยฮาร์มอนิก เราแนะนำให้ใช้เครื่องคิดเลขหรือโปรแกรม Excel
ค่าเฉลี่ยฮาร์มอนิกใน Excel คำนวณ ด้วยสูตร MEAN.ARMO นั่นคือ ในการคำนวณค่าเฉลี่ยฮาร์มอนิกของชุดข้อมูล คุณต้องคัดลอกลงในแผ่นงาน Excel และป้อนข้อมูลทั้งหมดลงในฟังก์ชัน MEAN.ARMO
ตัวอย่างเช่น หากต้องการหาค่าเฉลี่ยฮาร์มอนิกของแบบฝึกหัดที่เราแก้ข้างต้น ให้เขียนลงในเซลล์ Excel =MEDIA.ARMO(7;10;15;6;11)
คุณควรจำไว้ว่าหากค่าใดค่าหนึ่งเป็นศูนย์ฟังก์ชันจะส่งกลับข้อผิดพลาดเนื่องจากไม่สามารถระบุค่าเฉลี่ยฮาร์มอนิกของชุดค่าทางสถิติได้หากค่าใดค่าหนึ่งเป็นศูนย์