ค่าเฉลี่ยเลขคณิต

โดย ดร.เบนจามิน แอนเดอร์สัน สิงหาคม 6, 2023 สถิติ 0 ความคิดเห็น

ที่นี่เราจะอธิบายว่าค่าเฉลี่ยเลขคณิตคืออะไรและคำนวณอย่างไร คุณจะพบตัวอย่างค่าเฉลี่ยเลขคณิตและแม้แต่เครื่องคิดเลขเพื่อค้นหาค่าเฉลี่ยเลขคณิตของตัวอย่างทางสถิติใดๆ สุดท้าย คุณจะสามารถดูได้ว่าคุณสมบัติของค่าเฉลี่ยประเภทนี้คืออะไร และวิธีรับค่าเฉลี่ยเลขคณิตเมื่อข้อมูลที่จัดกลุ่มตามช่วงต่างๆ

ค่าเฉลี่ยเลขคณิตคืออะไร?

ค่าเฉลี่ยเลขคณิตเป็นคุณลักษณะค่ากลางของชุดข้อมูลทางสถิติ ในการคำนวณค่าเฉลี่ยเลขคณิต ค่าทั้งหมดจะถูกบวกและหารด้วยจำนวนข้อมูลทั้งหมด

นอกจากนี้ ค่าเฉลี่ยเลขคณิตยังเป็นหนึ่งในตัวบ่งชี้หลักที่ใช้ในการศึกษาทางสถิติของกลุ่มตัวอย่าง

สูตรสำหรับค่าเฉลี่ยเลขคณิตจึงเป็นดังนี้:

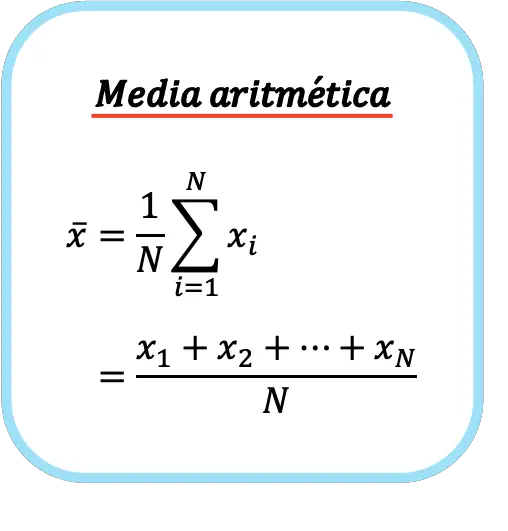
สัญลักษณ์ของค่าเฉลี่ยเลขคณิต คือแถบแนวนอนเหนือตัวอักษร x

$(\overline{x}).$

คุณยังสามารถแยกความแตกต่างของค่าเฉลี่ยตัวอย่างจากค่าเฉลี่ยประชากรด้วยสัญลักษณ์ค่าเฉลี่ยได้ โดยค่าเฉลี่ยของกลุ่มตัวอย่างจะแสดงด้วยสัญลักษณ์

$\overline{x}$

ในทางกลับกัน สำหรับค่าเฉลี่ยของประชากร เราใช้ตัวอักษรกรีก

$\mu.$

ควรสังเกตว่าค่าเฉลี่ยเลขคณิตของประชากรเทียบเท่ากับค่าที่คาดหวังของตัวแปรทางสถิติ

ค่าเฉลี่ยเลขคณิตหรือที่เรียกว่าค่าเฉลี่ยเลขคณิตไม่ใช่ค่าเฉลี่ยประเภทเดียวที่มีอยู่ ยังมีค่าเฉลี่ยถ่วงน้ำหนัก ค่าเฉลี่ยกำลังสอง ค่าเฉลี่ยเรขาคณิต และค่าเฉลี่ยฮาร์มอนิก และอื่นๆ อีกมากมาย คุณสามารถดูวิธีการคำนวณแต่ละรายการได้ในเครื่องมือค้นหาของเว็บไซต์ของเรา

วิธีการคำนวณค่าเฉลี่ยเลขคณิต

ในการคำนวณค่าเฉลี่ยเลขคณิตจะต้องดำเนินการตามขั้นตอนต่อไปนี้:

เพิ่มข้อมูลทางสถิติทั้งหมดจากตัวอย่าง
หารผลรวมก่อนหน้าด้วยจำนวนข้อมูลทั้งหมด
ผลลัพธ์ที่ได้คือค่าเฉลี่ยเลขคณิตของตัวอย่างทางสถิติ

👉 คุณสามารถใช้เครื่องคิดเลขด้านล่างเพื่อคำนวณค่าเฉลี่ยเลขคณิตของชุดข้อมูลใดก็ได้

ตัวอย่างการคำนวณค่าเฉลี่ยเลขคณิต

เมื่อพิจารณาคำจำกัดความของค่าเฉลี่ยเลขคณิตแล้ว เราจะมาดูวิธีหาค่าเฉลี่ยเลขคณิตของชุดข้อมูลโดยการแก้ตัวอย่างทีละขั้นตอน

นักเรียนได้เกรดต่อไปนี้ในระหว่างปีการศึกษา: ในวิชาคณิตศาสตร์ ได้ 9 คะแนน, ในภาษา 7 คะแนน, ประวัติศาสตร์ 6 คะแนน, เศรษฐศาสตร์ 8 คะแนน และวิทยาศาสตร์ 7.5 คะแนน ค่าเฉลี่ยเลขคณิตของเกรดทั้งหมดของคุณคือเท่าไร?

ในการหาค่าเฉลี่ยเลขคณิต เราต้องบวกเกรดทั้งหมดเข้าด้วยกันแล้วหารด้วยจำนวนวิชาทั้งหมดในรายวิชาซึ่งก็คือ 5 ดังนั้นเราจึงใช้สูตรค่าเฉลี่ยเลขคณิตดังนี้

$\displaystyle\overline{x}=\frac{1}{N}\sum_{i=1}^N x_i=\frac{x_1+x_2+x_3+x_4+x_5}{N}$

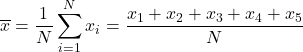
เราแทนที่ข้อมูลลงในสูตรและคำนวณค่าเฉลี่ยเลขคณิต:

$\overline{x}=\cfrac{9+7+5+8+7,5}{5}=7,3$

อย่างที่คุณเห็นในค่าเฉลี่ยเลขคณิต แต่ละค่ามีน้ำหนักเท่ากัน กล่าวคือ ข้อมูลแต่ละชิ้นมีน้ำหนักเท่ากันภายในข้อมูลทั้งหมด

เครื่องคิดเลขเฉลี่ยเลขคณิต

ป้อนข้อมูลจากตัวอย่างทางสถิติลงในเครื่องคิดเลขต่อไปนี้เพื่อคำนวณค่าเฉลี่ยเลขคณิต ข้อมูลต้องคั่นด้วยช่องว่างและป้อนโดยใช้จุดเป็นตัวคั่นทศนิยม

ค่าเฉลี่ยเลขคณิตสำหรับข้อมูลที่จัดกลุ่ม

ตามข้อมูลที่จัดกลุ่ม เราหมายถึงว่าข้อมูลมีโครงสร้างเป็นกลุ่มหรือตามช่วงเวลา ซึ่งมักเกิดขึ้นเมื่อขนาดตัวอย่างทางสถิติมีขนาดใหญ่มาก

ดังนั้นการคำนวณค่าเฉลี่ยเลขคณิตจะแตกต่างกันเล็กน้อยเมื่อข้อมูลถูกจัดกลุ่มเข้าด้วยกัน แม้ว่าแนวคิดจะเหมือนกันก็ตาม

ใน การคำนวณค่าเฉลี่ยเลขคณิตของข้อมูลที่จัดกลุ่ม ตามช่วงต่างๆ คะแนนชั้นเรียนของแต่ละกลุ่มจะต้องคูณด้วยความถี่สัมบูรณ์ แล้วหารด้วยผลรวมของความถี่สัมบูรณ์ทั้งหมด

$\displaystyle\overline{x}=\frac{\sum_{i=1}^N x_i\cdot f_i}{\sum_{i=1}^N f_i} =\frac{x_1\cdot f_1+ x_2\cdot f_2+\dots +x_N\cdot f_N}{N}$

หมายเหตุ: คะแนนชั้นเรียนของช่วงเวลาหนึ่งๆ คำนวณโดยการหารผลรวมของจุดสิ้นสุดของช่วงเวลาด้วยสอง ตัวอย่างเช่น บันทึกประจำชั้นเรียนของช่วง [3,7) จะเป็น:

$\cfrac{3+7}{2}=5$

เพื่อให้คุณสามารถดูวิธีการดำเนินการได้ ด้านล่างนี้คือแบบฝึกหัดที่ได้รับการแก้ไขเกี่ยวกับค่าเฉลี่ยเลขคณิตของข้อมูลที่จัดกลุ่มตามช่วงเวลา:

เราต้องการศึกษาน้ำหนักของกลุ่มทางสถิติ โดยสัมภาษณ์กลุ่มตัวแทนจำนวน 81 คน และได้ข้อมูลต่อไปนี้

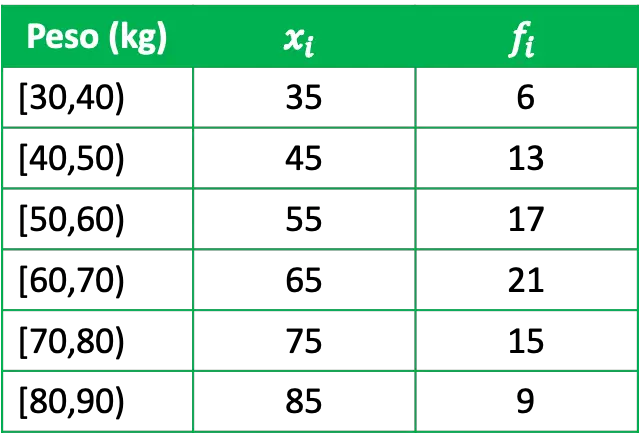
โดยที่ x _i คือคะแนนชั้นเรียนของแต่ละกลุ่ม และ f _i ความถี่สัมบูรณ์ กล่าวคือจำนวนคนที่มีน้ำหนักในช่วงเวลานี้

ในการหาค่าเฉลี่ยเลขคณิต จำเป็นต้องเพิ่มคอลัมน์ในตารางความถี่ซึ่งเป็นผลคูณของบันทึกย่อของชั้นเรียนด้วยความถี่สัมบูรณ์ตามลำดับ:

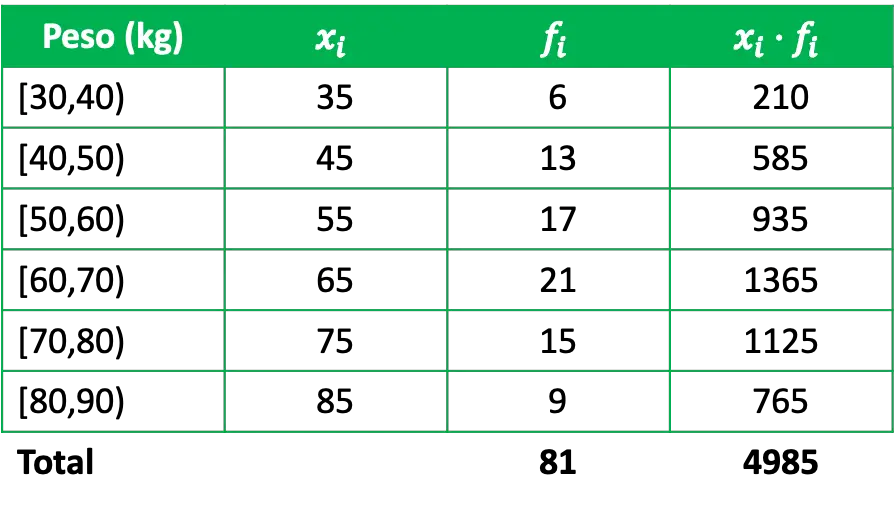
แบบฝึกหัดค่าเฉลี่ยเลขคณิตแก้ไขสำหรับข้อมูลที่จัดกลุ่ม

ดังนั้นในการคำนวณค่าเฉลี่ยเลขคณิตของข้อมูลที่จัดกลุ่มเพียงหารผลรวมของผลิตภัณฑ์ของบันทึกย่อชั้นเรียนด้วยความถี่ด้วยจำนวนข้อมูลทั้งหมด:

$\displaystyle\overline{x}=\frac{\sum_{i=1}^N x_i\cdot f_i}{\sum_{i=1}^N f_i} =\frac{4985}{81}=61,54 \text{ kg}$

คุณสมบัติของค่าเฉลี่ยเลขคณิต

ค่าเฉลี่ยเลขคณิตมีลักษณะดังต่อไปนี้:

ผลรวมของการเบี่ยงเบนของข้อมูลทั้งหมดในการแจกแจงจากค่าเฉลี่ยจะให้ผลลัพธ์เป็นศูนย์

$\sum_{i=1}^N\left(x_i-\overline{x}\right)=0$

ถ้าเราบวกจำนวนเท่ากันกับข้อมูลทั้งหมดในกลุ่มตัวอย่าง ค่าเฉลี่ยของกลุ่มตัวอย่างจะเพิ่มขึ้นตามจำนวนนั้น

สิ่งเดียวกันนี้เกิดขึ้นกับการคูณ ถ้าเราคูณค่าทั้งหมดในตัวอย่างด้วยตัวเลข ค่าเฉลี่ยตัวอย่างจะคูณด้วยตัวเลขนั้น

ค่าเฉลี่ยเลขคณิตสามารถคำนวณได้ใน ตัวแปรเชิงปริมาณ เท่านั้น กล่าวอีกนัยหนึ่ง คุณไม่สามารถหาค่าเฉลี่ยของตัวแปรเชิงคุณภาพได้

ค่าเฉลี่ยเลขคณิตจะเป็นค่าระหว่างค่าต่ำสุดและค่าสูงสุดของการแจกแจงเสมอ

$\text{min}\{x_1,x_2,...,x_N\}\leq \cfrac{x_1+\dots +x_N}{N}\leq \text{max}\{x_1,x_2,...,x_N\}$

ค่าเฉลี่ยประเภทนี้มีความอ่อนไหวต่อค่าที่สูงมากหรือต่ำมาก ส่งผลให้ค่าผิดปกติเปลี่ยนผลลัพธ์ของค่าเฉลี่ยเลขคณิตอย่างมีนัยสำคัญ

ค่าเฉลี่ยเลขคณิตของชุดข้อมูลจะเท่ากับหรือมากกว่าค่าเฉลี่ยเรขาคณิตของชุดข้อมูลเดียวกันเสมอ

$\displaystyle\frac{x_1+x_2+\dots+x_N}{N}\geq \sqrt[N]{x_1+x_2+\dots+x_N}$

คำนวณค่าเฉลี่ยเลขคณิตด้วย Excel

การคำนวณค่าเฉลี่ยเลขคณิตใน Excel นั้นง่ายมาก เนื่องจากคุณเพียงแค่ต้องป้อนข้อมูลลงในแผ่นงานและใช้ฟังก์ชัน AVERAGE

ตัวอย่างเช่น ในการหาค่าเฉลี่ยเลขคณิตของข้อมูลจากแบบฝึกหัดแรกที่เราอธิบายไปแล้ว เพียงคัดลอกข้อมูลทั้งหมดลงในเอกสาร Excel และเขียนสูตรต่อไปนี้ในเซลล์: =AVERAGE(9;7;5; 8;7 ,5) . ฟังก์ชันจะส่งกลับค่าเฉลี่ยเลขคณิตของข้อมูลซึ่งก็คือ 7.3

แน่นอนว่าการค้นหาค่าเฉลี่ยเลขคณิตของตัวเลขบางจำนวนด้วยโปรแกรม Excel นั้นเร็วกว่าการคำนวณด้วยมือ โดยเฉพาะอย่างยิ่งเมื่อขนาดตัวอย่างมีขนาดใหญ่มาก

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

สวัสดี ฉันชื่อเบนจามิน ศาสตราจารย์สถิติเกษียณอายุแล้ว และผันตัวมาเป็นครูสอนสถิติโดยเฉพาะ ด้วยประสบการณ์และความเชี่ยวชาญที่กว้างขวางในสาขาสถิติ ฉันกระตือรือร้นที่จะแบ่งปันความรู้ของฉันเพื่อเสริมศักยภาพนักเรียนผ่าน Statorials. รู้เพิ่มเติม