ค่าเบี่ยงเบนมาตรฐานใน google ชีต (ตัวอย่างและประชากร)
ค่าเบี่ยงเบนมาตรฐาน เป็นวิธีหนึ่งที่ใช้กันทั่วไปในการวัดการกระจายของค่าในชุดข้อมูล
ค่าเบี่ยงเบนมาตรฐานมีสองประเภทที่แตกต่างกันที่คุณสามารถคำนวณได้ ขึ้นอยู่กับประเภทของข้อมูลที่คุณใช้งาน
1. ส่วนเบี่ยงเบนมาตรฐานประชากร
คุณควรคำนวณค่าเบี่ยงเบนมาตรฐานของประชากรเมื่อชุดข้อมูลที่คุณใช้งานแสดงถึงประชากรทั้งหมด ซึ่งก็คือทุกค่าที่คุณสนใจ
สูตรในการคำนวณค่าเบี่ยงเบนมาตรฐานประชากรซึ่งเขียนแทนด้วย σ คือ:
σ = √ Σ(x i – μ) 2 / N
ทอง:
- Σ : สัญลักษณ์ที่หมายถึง “ผลรวม”
- x i : ค่า ที่ i ในชุดข้อมูล
- μ : ค่าเฉลี่ยประชากร
- N : ขนาดประชากร
2. ตัวอย่างค่าเบี่ยงเบนมาตรฐาน
คุณควรคำนวณค่าเบี่ยงเบนมาตรฐานของกลุ่มตัวอย่างเมื่อชุดข้อมูลที่คุณใช้งานอยู่แสดงถึงกลุ่มตัวอย่างที่นำมาจากประชากรที่สนใจจำนวนมากขึ้น
สูตรในการคำนวณค่าเบี่ยงเบนมาตรฐานตัวอย่างซึ่งเขียนว่า s คือ:
s = √ Σ(x i – x̄) 2 / (n – 1)
ทอง:
- Σ : สัญลักษณ์ที่หมายถึง “ผลรวม”
- x i : ค่า ที่ i ในชุดข้อมูล
- x̄ : ตัวอย่างหมายถึง
- n : ขนาดตัวอย่าง
ตัวอย่างต่อไปนี้แสดงวิธีคำนวณค่าเบี่ยงเบนมาตรฐานของกลุ่มตัวอย่างและประชากรใน Google ชีต
ตัวอย่างที่ 1: การคำนวณค่าเบี่ยงเบนมาตรฐานตัวอย่างใน Google ชีต
สมมติว่านักชีววิทยาต้องการสรุปค่าเบี่ยงเบนมาตรฐานของน้ำหนักของเต่าสายพันธุ์ใดสายพันธุ์หนึ่ง และเธอจึง สุ่มตัวอย่าง เต่า 20 ตัวจากประชากรทั้งหมด
เนื่องจากใช้ตัวอย่างในการประมาณค่าเบี่ยงเบนมาตรฐานของประชากร จึงสามารถคำนวณค่าเบี่ยงเบนมาตรฐานของกลุ่มตัวอย่างได้
ภาพหน้าจอต่อไปนี้แสดงวิธีใช้ฟังก์ชัน STDEV.S() เพื่อคำนวณค่าเบี่ยงเบนมาตรฐานตัวอย่าง:
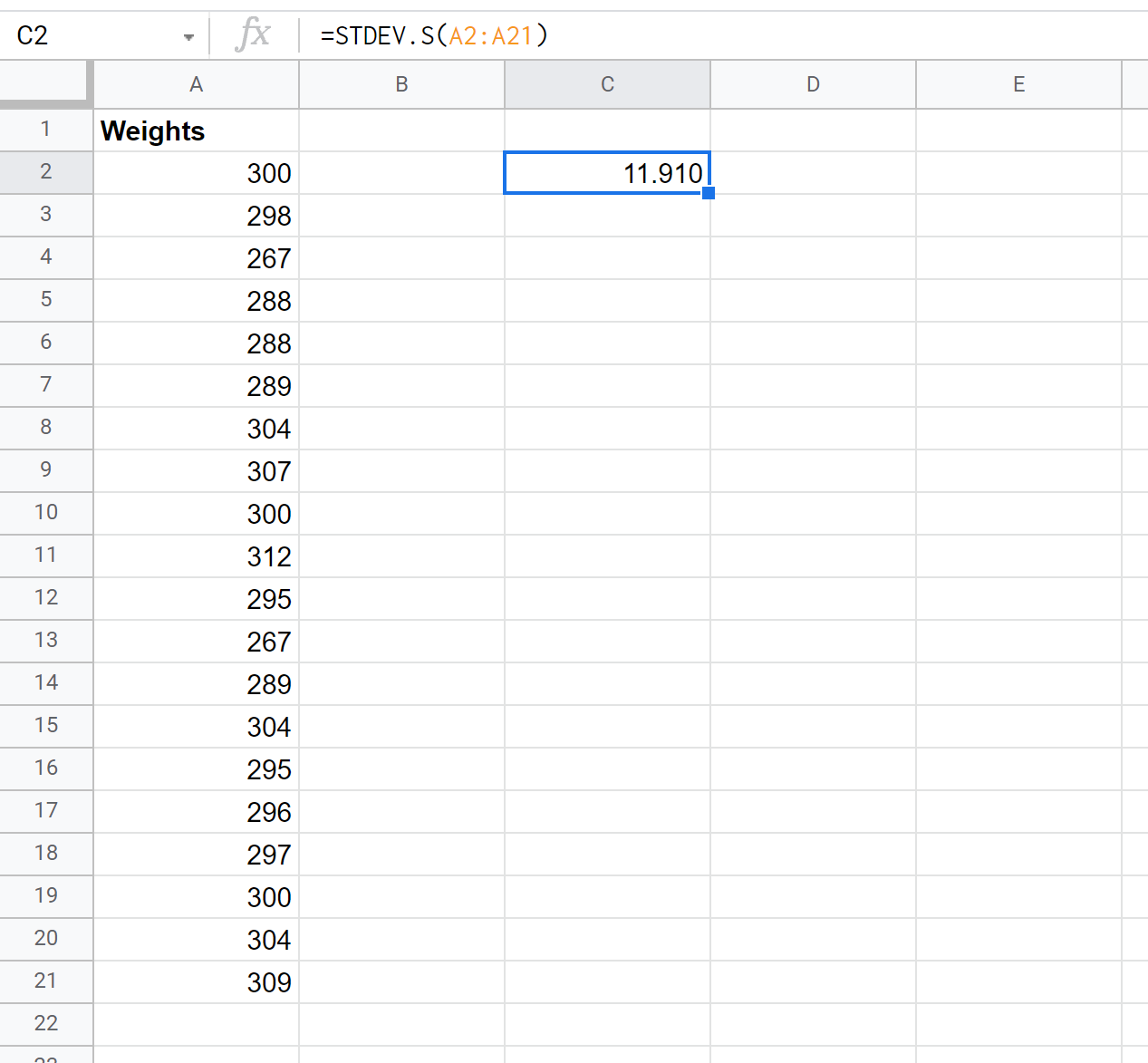
ค่าเบี่ยงเบนมาตรฐานตัวอย่างกลายเป็น 11.91
โปรดทราบว่า STDEV() จะส่งกลับค่าเบี่ยงเบนมาตรฐานตัวอย่างด้วย
ตัวอย่างที่ 2: การคำนวณค่าเบี่ยงเบนมาตรฐานของประชากรใน Google ชีต
สมมติว่าโค้ชบาสเกตบอลต้องการสรุปค่าเบี่ยงเบนมาตรฐานของคะแนนที่ผู้เล่น 12 คนในทีมของเขาทำได้
เนื่องจากเขาสนใจเฉพาะคะแนนที่ผู้เล่นทำได้ ไม่ใช่ผู้เล่นคนอื่นในทีมอื่น เขาจึงสามารถคำนวณค่าเบี่ยงเบนมาตรฐานของประชากรได้
ภาพหน้าจอต่อไปนี้แสดงวิธีใช้ฟังก์ชัน STDEV.P() เพื่อคำนวณค่าเบี่ยงเบนมาตรฐานของประชากร:
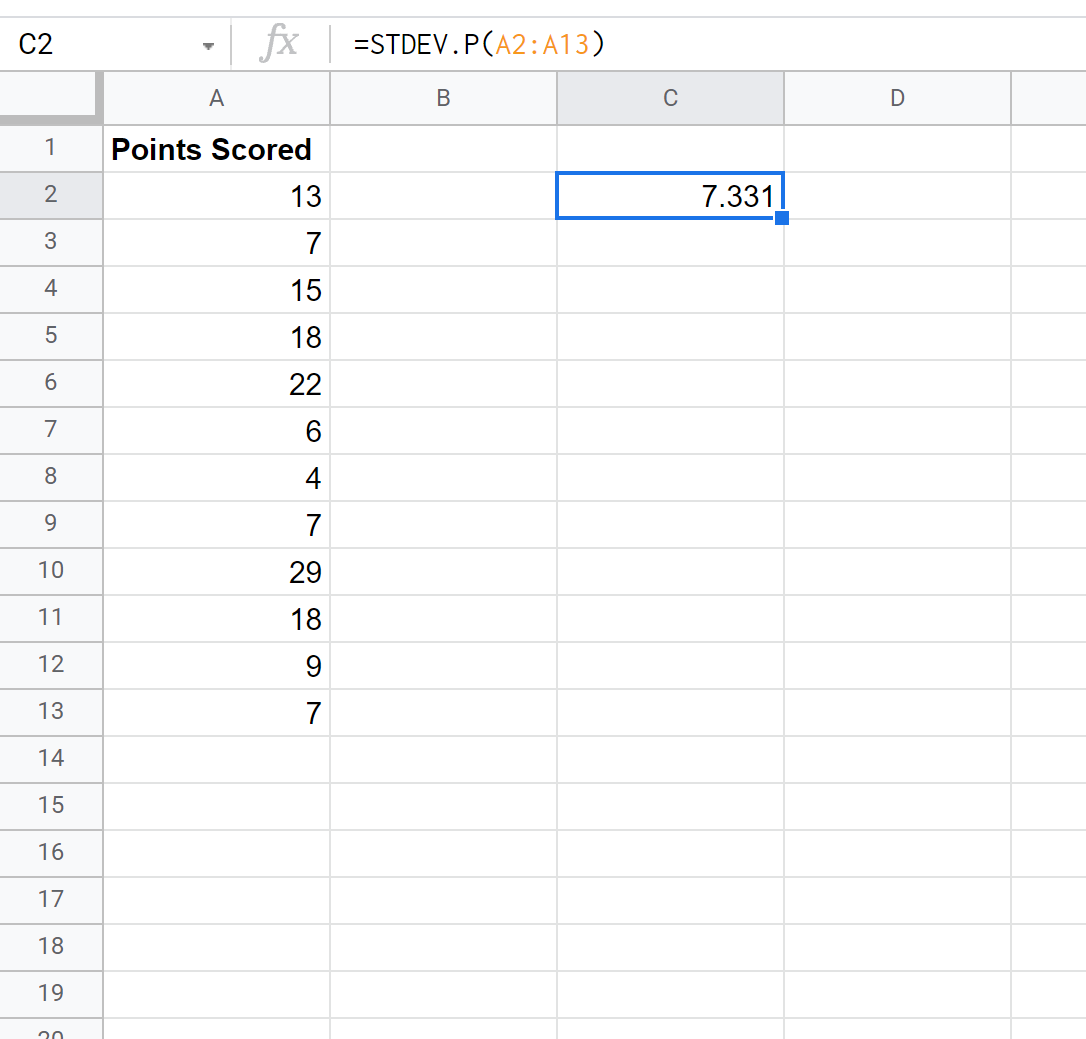
ค่าเบี่ยงเบนมาตรฐานของประชากรกลายเป็น 7,331
แหล่งข้อมูลเพิ่มเติม
บทช่วยสอนต่อไปนี้ให้ข้อมูลเพิ่มเติมเกี่ยวกับค่าเบี่ยงเบนมาตรฐาน:
- ประชากรเทียบกับ ตัวอย่างค่าเบี่ยงเบนมาตรฐาน: เมื่อใดควรใช้แต่ละรายการ
- สัมประสิทธิ์ของการแปรผันกับส่วนเบี่ยงเบนมาตรฐาน: ความแตกต่าง
- เหตุใดค่าเบี่ยงเบนมาตรฐานจึงมีความสำคัญ
บทช่วยสอนต่อไปนี้จะอธิบายวิธีคำนวณเมตริกสเปรดอื่นๆ ใน Google ชีต