การทดสอบ augmented dickey-fuller ใน python (พร้อมตัวอย่าง)
อนุกรมเวลาจะเรียกว่า “คงที่” หากไม่มีแนวโน้ม นำเสนอความแปรปรวนคงที่ตลอดเวลา และมีโครงสร้างความสัมพันธ์อัตโนมัติที่คงที่ตลอดเวลา
วิธีหนึ่งในการทดสอบว่าอนุกรมเวลาคงที่หรือไม่คือทำการ ทดสอบ Augmented Dickey–Fuller ซึ่งใช้สมมติฐานว่างและสมมุติฐานทางเลือกต่อไปนี้
H 0 : อนุกรมเวลาไม่คงที่ กล่าวอีกนัยหนึ่ง โครงสร้างของมันขึ้นอยู่กับเวลา และการแปรผันของมันไม่คงที่เมื่อเวลาผ่านไป
H A : อนุกรมเวลาหยุดนิ่ง
หาก ค่า p ของการทดสอบต่ำกว่าระดับนัยสำคัญที่กำหนด (เช่น α = 0.05) เราก็สามารถปฏิเสธสมมติฐานว่างและสรุปได้ว่าอนุกรมเวลาเป็นแบบคงที่
ตัวอย่างทีละขั้นตอนต่อไปนี้แสดงวิธีดำเนินการทดสอบ Augmented Dickey-Fuller ใน Python สำหรับอนุกรมเวลาที่กำหนด
ตัวอย่าง: การทดสอบ Augmented Dickey-Fuller ใน Python
สมมติว่าเรามีข้อมูลอนุกรมเวลาต่อไปนี้ใน Python:
data = [3, 4, 4, 5, 6, 7, 6, 6, 7, 8, 9, 12, 10]
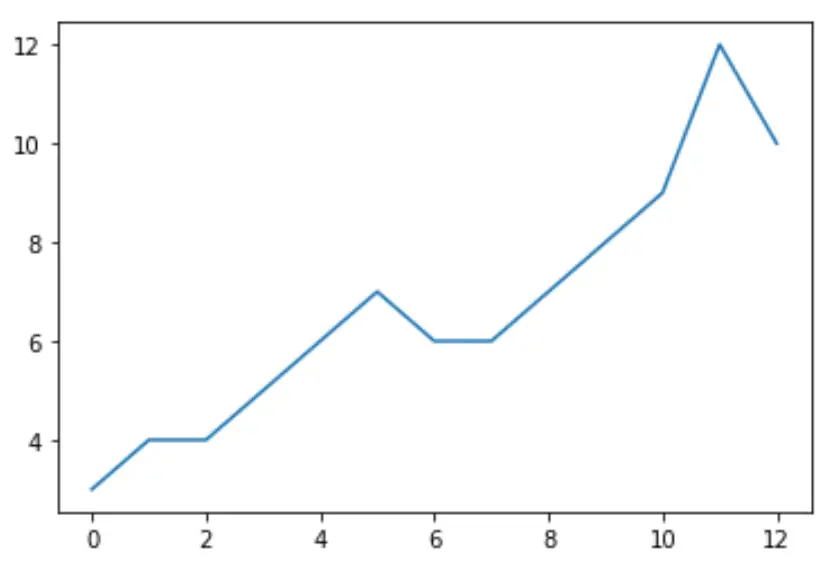
ก่อนที่จะทำการทดสอบ Augmented Dickey-Fuller กับข้อมูล เราสามารถสร้างพล็อตด่วนเพื่อแสดงภาพข้อมูลได้:
import matplotlib. pyplot as plt plt. plot (data)
ในการทำการทดสอบ Augmented Dickey-Fuller เราสามารถใช้ฟังก์ชัน adfuller() จากไลบรารี statsmodels ก่อนอื่น เราต้องติดตั้ง statsmodels:
pip install statsmodels
จากนั้นเราสามารถใช้โค้ดต่อไปนี้เพื่อทำการทดสอบ Augmented Dickey-Fuller:
from statsmodels. tsa . stattools import adfuller #perform augmented Dickey-Fuller test adfuller(data) (-0.9753836234744063, 0.7621363564361013, 0, 12, {'1%': -4.137829282407408, '5%': -3.1549724074074077, '10%': -2.7144769444444443}, 31.2466098872313)
ต่อไปนี้เป็นวิธีตีความค่าที่สำคัญที่สุดของผลลัพธ์:
- สถิติการทดสอบ: -0.97538
- ค่า P: 0.7621
เนื่องจากค่า p ไม่น้อยกว่า 0.05 เราจึงไม่สามารถปฏิเสธสมมติฐานว่างได้
ซึ่งหมายความว่าอนุกรมเวลาไม่คงที่ กล่าวอีกนัยหนึ่ง โครงสร้างของมันขึ้นอยู่กับเวลา และการแปรผันของมันไม่คงที่เมื่อเวลาผ่านไป
แหล่งข้อมูลเพิ่มเติม
วิธีพล็อตอนุกรมเวลาใน Matplotlib
วิธีพล็อตหลายซีรีย์จาก Pandas DataFrame
วิธีดำเนินการทดสอบแนวโน้ม Mann-Kendall ใน Python