วิธีการคำนวณช่วงความมั่นใจใน excel
ช่วงความเชื่อมั่น คือช่วงของค่าที่น่าจะมีพารามิเตอร์ประชากรที่มีระดับความเชื่อมั่นที่แน่นอน คำนวณตามสูตรทั่วไปต่อไปนี้:
ช่วงความเชื่อมั่น = (การประมาณจุด) +/- (ค่าวิกฤต)* (ข้อผิดพลาดมาตรฐาน)
สูตรนี้สร้างช่วงที่มีขอบเขตล่างและขอบเขตบน ซึ่งน่าจะประกอบด้วยพารามิเตอร์ประชากรที่มีระดับความเชื่อมั่นในระดับหนึ่ง:
ช่วงความเชื่อมั่น = [ขีดจำกัดล่าง, ขีดจำกัดบน]
บทช่วยสอนนี้จะอธิบายวิธีการคำนวณช่วงความเชื่อมั่นต่อไปนี้ใน Excel:
1. ช่วงความเชื่อมั่นสำหรับค่าเฉลี่ย
2. ช่วงความเชื่อมั่นสำหรับผลต่างของค่าเฉลี่ย
3. ช่วงความเชื่อมั่นตามสัดส่วน
4. ช่วงความเชื่อมั่นสำหรับส่วนต่างของสัดส่วน
ไปกันเถอะ!
ตัวอย่างที่ 1: ช่วงความเชื่อมั่นสำหรับค่าเฉลี่ย
เราใช้สูตรต่อไปนี้เพื่อคำนวณ ช่วงความเชื่อมั่นสำหรับค่าเฉลี่ย :
ช่วงความเชื่อมั่น = x +/- z*(s/√n)
ทอง:
- x : หมายถึงตัวอย่าง
- z: ค่า z ที่เลือก
- s: ค่าเบี่ยงเบนมาตรฐานตัวอย่าง
- n: ขนาดตัวอย่าง
ตัวอย่าง: สมมติว่าเราสุ่มตัวอย่างเต่าโดยมีข้อมูลต่อไปนี้:
- ขนาดตัวอย่าง n = 25
- น้ำหนักตัวอย่างเฉลี่ย x = 300
- ตัวอย่างค่าเบี่ยงเบนมาตรฐาน s = 18.5
ภาพหน้าจอต่อไปนี้แสดงวิธีคำนวณช่วงความเชื่อมั่น 95% สำหรับน้ำหนักเฉลี่ยที่แท้จริงของประชากรเต่า:
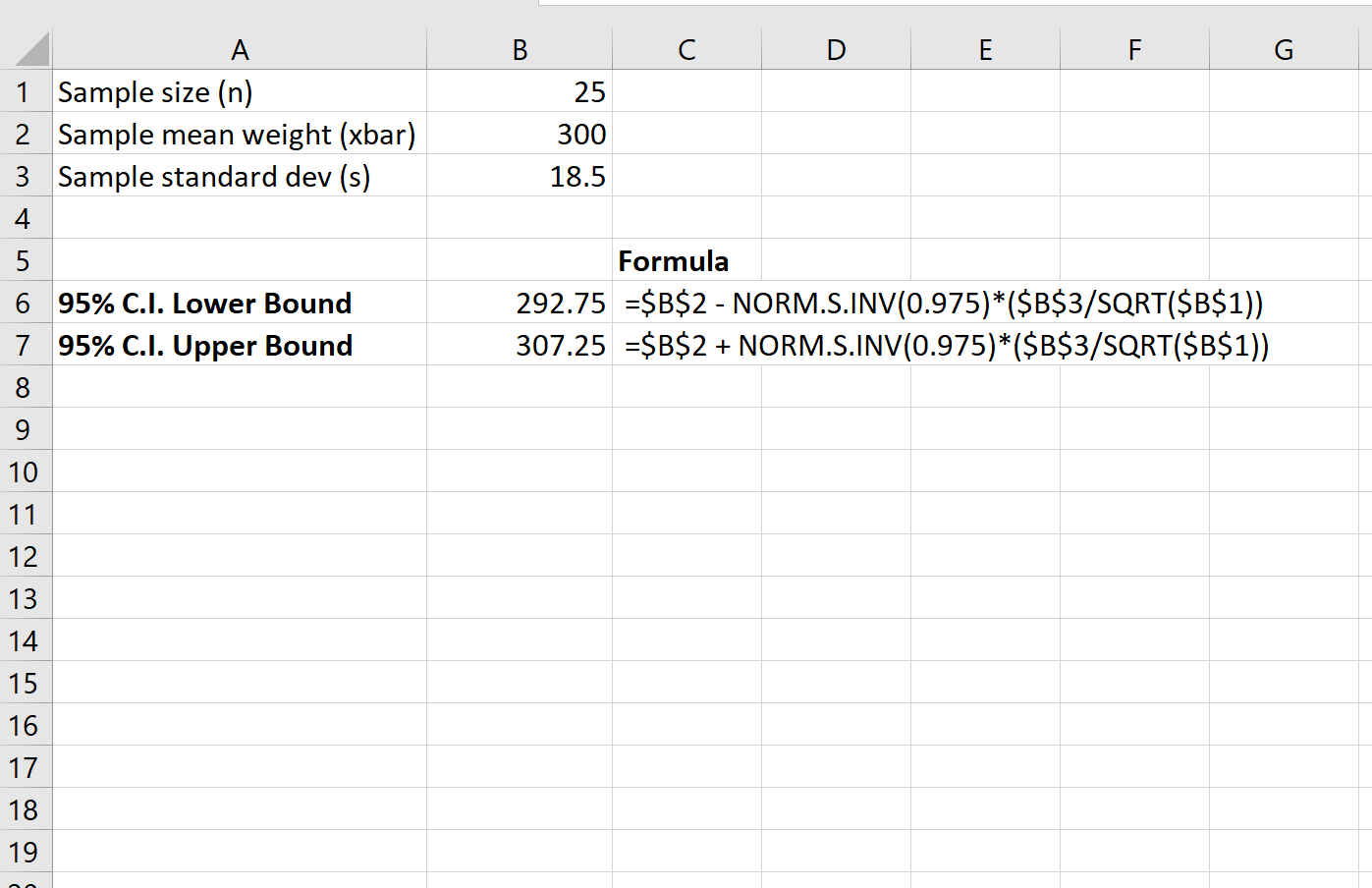
ช่วงความเชื่อมั่น 95% สำหรับน้ำหนักประชากรเต่าเฉลี่ยที่แท้จริงคือ [292.75, 307.25]
ตัวอย่างที่ 2: ช่วงความเชื่อมั่นสำหรับผลต่างในค่าเฉลี่ย
เราใช้สูตรต่อไปนี้เพื่อคำนวณช่วงความเชื่อมั่นสำหรับ ผลต่างในค่าเฉลี่ยประชากร :
ช่วงความเชื่อมั่น = ( x 1 – x 2 ) +/- t*√((s p 2 /n 1 ) + (s p 2 /n 2 ))
ทอง:
- x 1 , x 2 : ค่าเฉลี่ยของกลุ่มตัวอย่าง 1, ค่าเฉลี่ยของกลุ่มตัวอย่าง 2
- t: ค่า t-critical ขึ้นอยู่กับระดับความเชื่อมั่นและระดับความเป็นอิสระ (n 1 + n 2 -2)
- s p 2 : ความแปรปรวนรวม คำนวณเป็น ((n 1 -1)s 1 2 + (n 2 -1)s 2 2 ) / (n 1 +n 2 -2)
- t: ค่า t-วิกฤต
- n 1 , n 2 : ขนาดตัวอย่าง 1, ขนาดตัวอย่าง 2
ตัวอย่าง: สมมติว่าเราต้องการประมาณค่าความแตกต่างของน้ำหนักเฉลี่ยระหว่างเต่าสองสายพันธุ์ที่แตกต่างกัน เราจึงสุ่มตัวอย่างเต่าจำนวน 15 ตัวจากประชากรแต่ละกลุ่ม นี่คือข้อมูลสรุปสำหรับแต่ละตัวอย่าง:
ตัวอย่างที่ 1:
- x1 = 310
- ส 1 = 18.5
- ไม่มี 1 = 15
ตัวอย่างที่ 2:
- x2 = 300
- s2 = 16.4
- n2 = 15
ภาพหน้าจอต่อไปนี้แสดงวิธีคำนวณช่วงความเชื่อมั่น 95% สำหรับความแตกต่างที่แท้จริงในค่าเฉลี่ยประชากร:
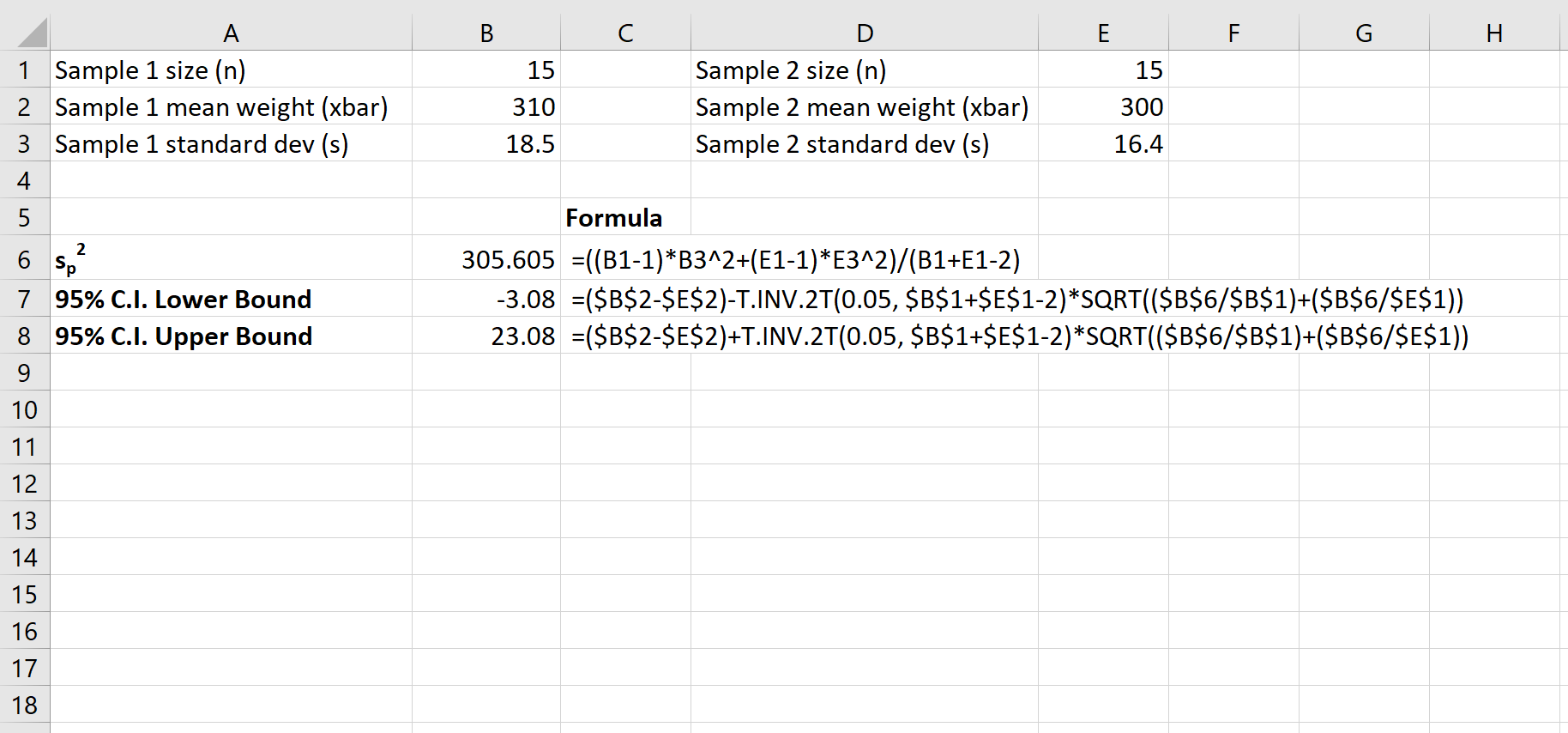
ช่วงความเชื่อมั่น 95% สำหรับความแตกต่างที่แท้จริงระหว่างค่าเฉลี่ยประชากรคือ [-3.08, 23.08]
ตัวอย่างที่ 3: ช่วงความเชื่อมั่นสำหรับสัดส่วน
เราใช้สูตรต่อไปนี้เพื่อคำนวณ ช่วงความเชื่อมั่นสำหรับสัดส่วน :
ช่วงความเชื่อมั่น = p +/- z*√ p(1-p) / n
ทอง:
- p: สัดส่วนตัวอย่าง
- z: ค่า z ที่เลือก
- n: ขนาดตัวอย่าง
ตัวอย่าง: สมมติว่าเราต้องการประมาณสัดส่วนของผู้อยู่อาศัยในเขตหนึ่งที่สนับสนุนกฎหมายบางข้อ เราสุ่มตัวอย่างผู้อยู่อาศัย 100 คน และถามพวกเขาว่าจุดยืนของพวกเขาในด้านกฎหมายคืออะไร นี่คือผลลัพธ์:
- ขนาดตัวอย่าง n = 100
- สัดส่วนสนับสนุนกฎหมาย p = 0.56
ภาพหน้าจอต่อไปนี้แสดงวิธีคำนวณช่วงความเชื่อมั่น 95% สำหรับสัดส่วนที่แท้จริงของผู้อยู่อาศัยทั่วทั้งเทศมณฑลที่สนับสนุนกฎหมาย:
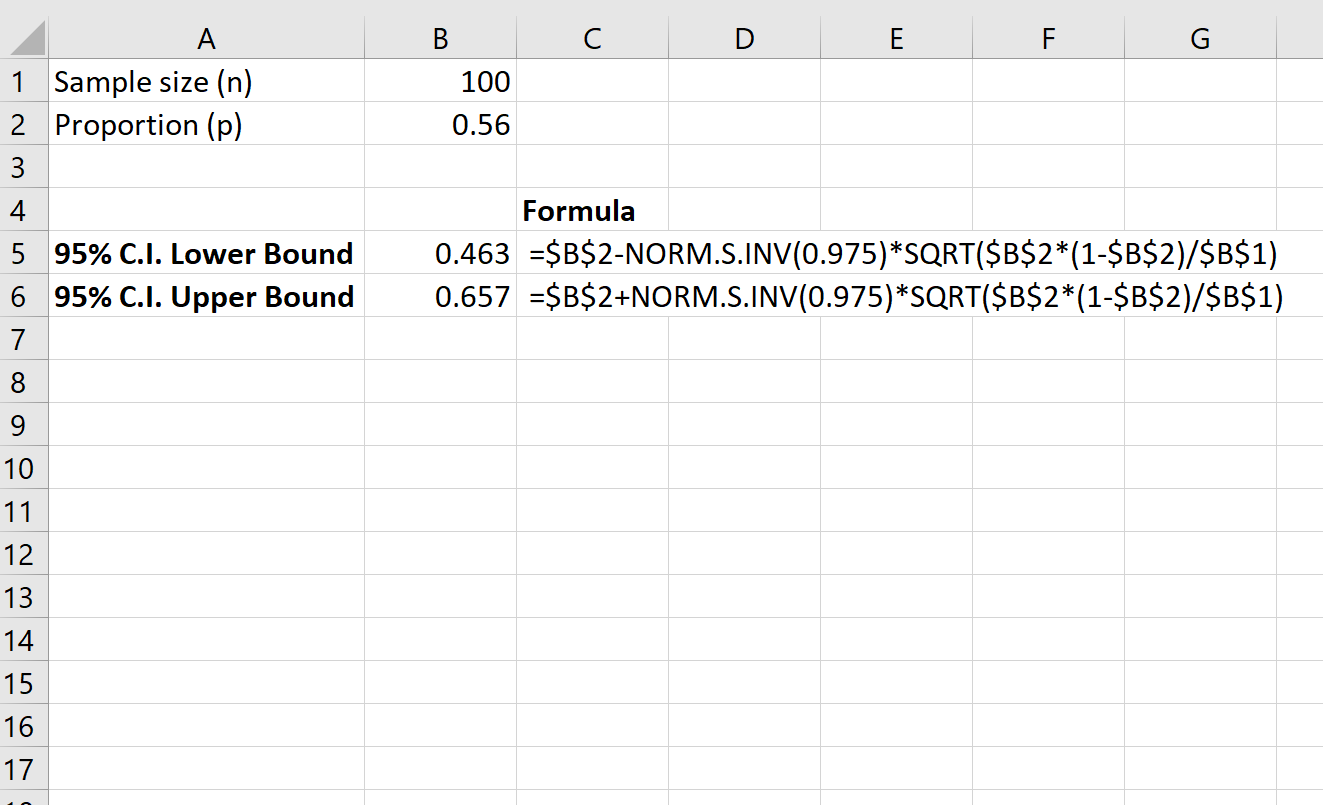
ช่วงความเชื่อมั่น 95% สำหรับสัดส่วนที่แท้จริงของผู้อยู่อาศัยทั่วทั้งมณฑลที่สนับสนุนกฎหมายคือ [.463, .657]
ตัวอย่างที่ 4: ช่วงความเชื่อมั่นสำหรับความแตกต่างในสัดส่วน
เราใช้สูตรต่อไปนี้เพื่อคำนวณ ช่วงความเชื่อมั่นสำหรับส่วนต่างของสัดส่วน :
ช่วงความเชื่อมั่น = (p 1 –p 2 ) +/- z*√(p 1 (1-p 1 )/n 1 + p 2 (1-p 2 )/n 2 )
ทอง:
- p 1 , p 2 : สัดส่วนของกลุ่มตัวอย่าง 1, สัดส่วนของกลุ่มตัวอย่าง 2
- z: ค่าวิกฤต z ตามระดับความเชื่อมั่น
- n 1 , n 2 : ขนาดตัวอย่าง 1, ขนาดตัวอย่าง 2
ตัวอย่าง: สมมติว่าเราต้องการประมาณความแตกต่างระหว่างสัดส่วนของผู้อยู่อาศัยที่สนับสนุนกฎหมายบางอย่างในเคาน์ตี้ A เทียบกับสัดส่วนที่สนับสนุนกฎหมายในเคาน์ตี้ B นี่คือข้อมูลสรุปสำหรับแต่ละตัวอย่าง:
ตัวอย่างที่ 1:
- ไม่มี 1 = 100
- p 1 = 0.62 (เช่น ประชากร 62 คนจาก 100 คนสนับสนุนกฎหมาย)
ตัวอย่างที่ 2:
- n2 = 100
- p 2 = 0.46 (เช่น ประชากร 46 คนจาก 100 คนสนับสนุนกฎหมาย)
ภาพหน้าจอต่อไปนี้แสดงวิธีคำนวณช่วงความเชื่อมั่น 95% สำหรับความแตกต่างที่แท้จริงในสัดส่วนของผู้อยู่อาศัยที่สนับสนุนกฎหมายระหว่างเทศมณฑล:
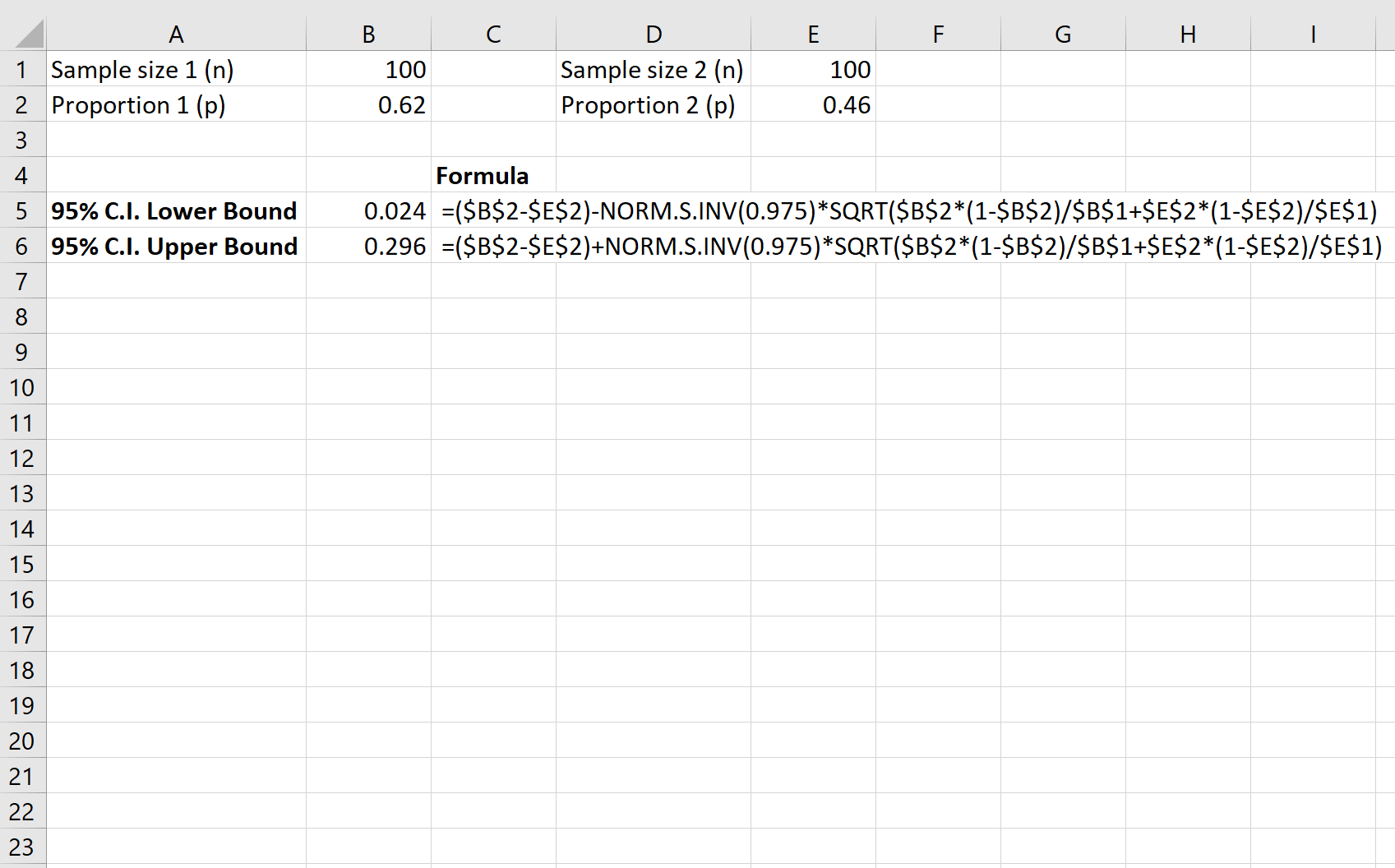
ช่วงความเชื่อมั่น 9.5% สำหรับความแตกต่างที่แท้จริงในสัดส่วนของผู้อยู่อาศัยที่สนับสนุนกฎหมายระหว่างเทศมณฑลคือ [0.024, 0.296]
คุณสามารถค้นหาบทช่วยสอน Excel เพิ่มเติมได้ ที่นี่
เกี่ยวกับผู้แต่ง
ดร.เบนจามิน แอนเดอร์สัน
สวัสดี ฉันชื่อเบนจามิน ศาสตราจารย์สถิติเกษียณอายุแล้ว และผันตัวมาเป็นครูสอนสถิติโดยเฉพาะ ด้วยประสบการณ์และความเชี่ยวชาญที่กว้างขวางในสาขาสถิติ ฉันกระตือรือร้นที่จะแบ่งปันความรู้ของฉันเพื่อเสริมศักยภาพนักเรียนผ่าน Statorials. รู้เพิ่มเติม