ตัวแปรตามและอิสระ

บทความนี้จะอธิบายว่าตัวแปรตามและตัวแปรอิสระคืออะไร ดังนั้น คุณจะพบว่าอะไรคือความแตกต่างระหว่างตัวแปรตามและตัวแปรอิสระ จะทราบได้อย่างไรว่าตัวแปรตามและตัวแปรอิสระใด นอกจากนี้ ยังมีการนำเสนอตัวอย่างหลายตัวอย่างของตัวแปรประเภทนี้ด้วย

ตัวแปรตามและตัวแปรอิสระคืออะไร?

ตัวแปรตาม คือตัวแปรที่มีค่าขึ้นอยู่กับตัวแปรอื่นซึ่งเป็น ตัวแปรอิสระ ดังนั้น ความแตกต่างระหว่างตัวแปรตามและตัวแปรอิสระ ก็คือ ตัวแปรอิสระไม่ได้ขึ้นอยู่กับตัวแปรอื่นใด แต่ตัวแปรตามขึ้นอยู่กับค่าของตัวแปรอิสระ

บนกราฟ ตัวแปรอิสระจะแสดงด้วยตัวอักษร x บน Abscissa (แกนนอน) ในขณะที่ตัวแปรตามแสดงด้วยตัวอักษร y บนพิกัด (แกนตั้ง)

ตัวอย่างเช่น หากในการศึกษาทางสถิติเราวิเคราะห์ความสัมพันธ์ระหว่างเกรดที่ได้รับกับชั่วโมงการศึกษาที่ทุ่มเท ชั่วโมงการศึกษาที่ทุ่มเทจะเป็นตัวแปรอิสระและเกรดที่ได้รับจะเป็นตัวแปรตาม เนื่องจากเกรดที่ได้รับขึ้นอยู่กับชั่วโมงเรียน ไม่ใช่อย่างอื่น

ตัวอย่างของตัวแปรตามและตัวแปรอิสระ

ในหัวข้อที่แล้ว เราเห็นคำจำกัดความของตัวแปรตามและตัวแปรอิสระ ดังนั้นตอนนี้เราจะดูตัวอย่างสิบตัวอย่างของตัวแปรประเภทนี้เพื่อทำความเข้าใจความหมายของมันให้ดียิ่งขึ้น

1. เวลาที่ใช้ในการศึกษา (ตัวแปรอิสระ) ส่งผลต่อเกรดที่ได้รับ (ตัวแปรตาม)
2. ราคาของผลิตภัณฑ์ (ตัวแปรอิสระ) จะเปลี่ยนจำนวนผู้ที่ยินดีซื้อผลิตภัณฑ์ (ตัวแปรตาม)
3. สุขภาพของบุคคล (ตัวแปรตาม) ขึ้นอยู่กับการรับประทานอาหาร (ตัวแปรอิสระ)
4. อัตราการเต้นของหัวใจของบุคคล (ตัวแปรตาม) จะขึ้นอยู่กับความสูงของพวกเขา (ตัวแปรอิสระ)
5. อุณหภูมิโดยรอบ (ตัวแปรอิสระ) มีอิทธิพลต่อจำนวนไฟป่า (ตัวแปรตาม)
6. ระดับความพึงพอใจของลูกค้า (ตัวแปรตาม) พัฒนาตามคุณภาพของบริการที่ให้ (ตัวแปรอิสระ)
7. การโฆษณาผลิตภัณฑ์ (ตัวแปรอิสระ) มีผลกระทบต่อจำนวนยอดขายของผลิตภัณฑ์ดังกล่าว (ตัวแปรตาม)
8. ปริมาณของสารก่อมลพิษที่ปล่อยออกมาจากประเทศหนึ่งๆ (ตัวแปรตาม) ขึ้นอยู่กับการผลิตทางอุตสาหกรรมของประเทศนี้ (ตัวแปรอิสระ)
9. เงินเดือนของคนขับรถแท็กซี่ (ตัวแปรอิสระ) ขึ้นอยู่กับจำนวนเที่ยวที่เขาเดินทาง (ตัวแปรอิสระ)
10. จำนวนประชากรในเมือง (ตัวแปรอิสระ) เชื่อมโยงกับจำนวนรถแท็กซี่ในเมือง (ตัวแปรตาม)

โปรดทราบว่าตัวแปรนั้นขึ้นอยู่กับหรือขึ้นอยู่กับบริบท เพราะขึ้นอยู่กับการสืบสวน ตัวแปรนั้นจะทำหน้าที่เป็นสาเหตุหรือผลกระทบของความสัมพันธ์

แบบฝึกหัดตัวแปรตามและอิสระ

ในกรณีต่อไปนี้ ข้อใดเป็นตัวแปรตาม และข้อใดเป็นตัวแปรอิสระ

1. จำนวนประชากรในเมือง – จำนวนรถโดยสารสาธารณะ
2. อายุรถ – สภาพรถ
3. จำนวนยุง – อุณหภูมิโดยรอบ
4. จำนวนวันที่ฝนตกต่อเดือน – ความต้องการร่ม

1. ตัวแปรตาม: จำนวนรถโดยสารสาธารณะ – ตัวแปรอิสระ: จำนวนผู้อยู่อาศัยในเมือง
2. ตัวแปรตาม: สภาพของรถ – ตัวแปรอิสระ: อายุของรถ
3. ตัวแปรตาม: จำนวนยุง – ตัวแปรอิสระ: อุณหภูมิแวดล้อม
4. ตัวแปรตาม: ความต้องการร่ม – ตัวแปรอิสระ: จำนวนวันที่ฝนตกต่อเดือน

ตัวแปรตามและอิสระในวิชาคณิตศาสตร์

ในทางคณิตศาสตร์ ความสัมพันธ์ระหว่างเหตุและผลมักจะถูกจำลองโดยใช้ตัวแปรอิสระและตัวแปรตาม ดังนั้นฟังก์ชันจะกำหนดความสัมพันธ์ทางคณิตศาสตร์ที่มีอยู่ระหว่างตัวแปรตามและตัวแปรอิสระ

ตัวแปรตามมักจะแสดงด้วยตัวอักษร y ในทางกลับกัน ตัวอักษร x โดยทั่วไปจะใช้เพื่อระบุตัวแปรอิสระ

ตัวอย่างเช่น ฟังก์ชัน y=2x บ่งชี้ว่าเมื่อตัวแปรอิสระ x เพิ่มขึ้นหนึ่งหน่วย ตัวแปรตาม y จะเพิ่มขึ้นสองเท่า

หากต้องการเรียนรู้เพิ่มเติมเกี่ยวกับฟังก์ชันทางคณิตศาสตร์ คุณสามารถเยี่ยมชมเว็บไซต์พันธมิตรของเรา function.xyz

ตัวแปรตามและอิสระในสถิติ

อย่างไรก็ตาม ในความเป็นจริง เป็นเรื่องยากมากที่จะค้นหาความสัมพันธ์ระหว่างตัวแปรสองตัวที่สามารถกำหนดได้ด้วยฟังก์ชันทางคณิตศาสตร์ที่แน่นอน เนื่องจากบางครั้งค่าที่เท่ากันของตัวแปรอิสระจะส่งผลให้ค่าของตัวแปรตามต่างกันออกไป

ตัวอย่างเช่น บางครั้งหากเรียนมากขึ้นเราจะได้เกรดที่ต่ำกว่า หรือในทางกลับกัน หากเรียนน้อยเราจะได้เกรดที่ดีขึ้น ดังนั้นจำนวนชั่วโมงที่เราทุ่มเทให้กับการเรียนจึงไม่ใช่ปัจจัยเดียวที่มีอิทธิพลต่อเกรดที่ได้รับ แต่ยังอาจแตกต่างกันไปขึ้นอยู่กับความยากของการสอบหรือความยากของเนื้อหาที่เรียนด้วย

ด้วยเหตุนี้ ในสถิติ จึงมีการทดลองหลายอย่างเพื่อพิจารณาว่ามีความสัมพันธ์ระหว่างตัวแปรสองตัวหรือไม่ โดยตัวแปรตัวหนึ่งจะเป็นตัวแปรอิสระและอีกตัวเป็นตัวแปรตาม จากนั้น ผลลัพธ์ที่ได้สามารถแสดงเป็นกราฟิกเพื่อตรวจสอบว่าตัวแปรเชื่อมโยงกันหรือไม่ และหากเป็นเช่นนั้น ให้ดูความสัมพันธ์ประเภทใด (บวก ลบ เชิงเส้น เอ็กซ์โปเนนเชียล ฯลฯ)

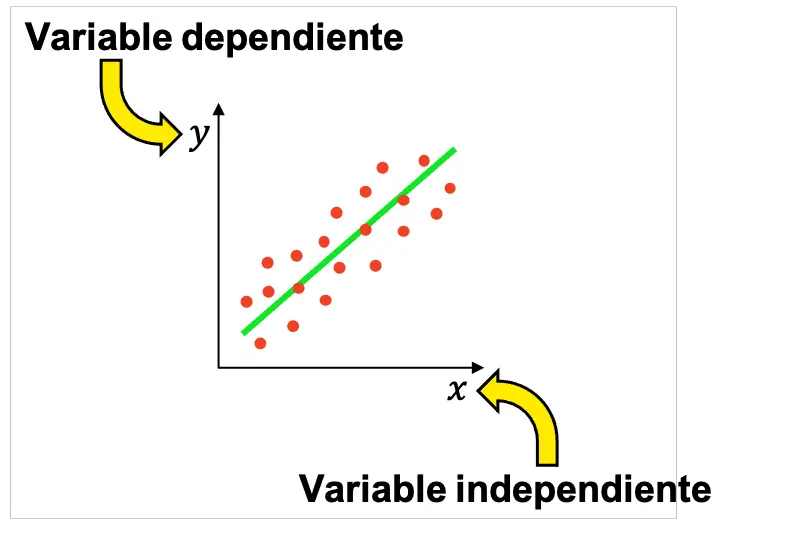
โปรดทราบว่าในแบบสำรวจอาจมีตัวแปรอิสระมากกว่าหนึ่งตัว แม้ว่าการศึกษาทางสถิติขั้นพื้นฐานที่สุดจะดำเนินการโดยใช้ตัวแปรอิสระหนึ่งตัวและตัวแปรตามหนึ่งตัวก็ตาม

เมื่อดำเนินการศึกษาทางสถิติแล้ว ฟังก์ชันทางคณิตศาสตร์สามารถคำนวณเพื่อทำการประมาณและจำลองความสัมพันธ์ระหว่างตัวแปรต่างๆ ได้ โดยปกติแล้วแบบจำลองทางสถิติจะถูกสร้างขึ้นก่อน จากนั้นจึงสร้างแบบจำลองทางคณิตศาสตร์ขึ้นมา