ตัวแปรที่น่าสับสนคืออะไร? (คำจำกัดความ & #038; ตัวอย่าง)

ในการทดลองใดๆ มีตัวแปรหลักอยู่ 2 ตัวแปร:

ตัวแปรอิสระ: ตัวแปรที่ผู้ทดลองแก้ไขหรือควบคุมเพื่อให้สามารถสังเกตผลกระทบของตัวแปรตามได้

ตัวแปรตาม: ตัวแปรที่วัดในการทดลองที่ “ขึ้นอยู่กับ” ตัวแปรอิสระ

นักวิจัยมักสนใจที่จะทำความเข้าใจว่าการเปลี่ยนแปลงของตัวแปรอิสระส่งผลต่อตัวแปรตามอย่างไร

อย่างไรก็ตาม บางครั้งอาจเกิดขึ้นได้ว่าตัวแปรที่สามไม่ได้ถูกนำมาพิจารณา และอาจส่งผลต่อความสัมพันธ์ระหว่างตัวแปรทั้งสองที่ศึกษา

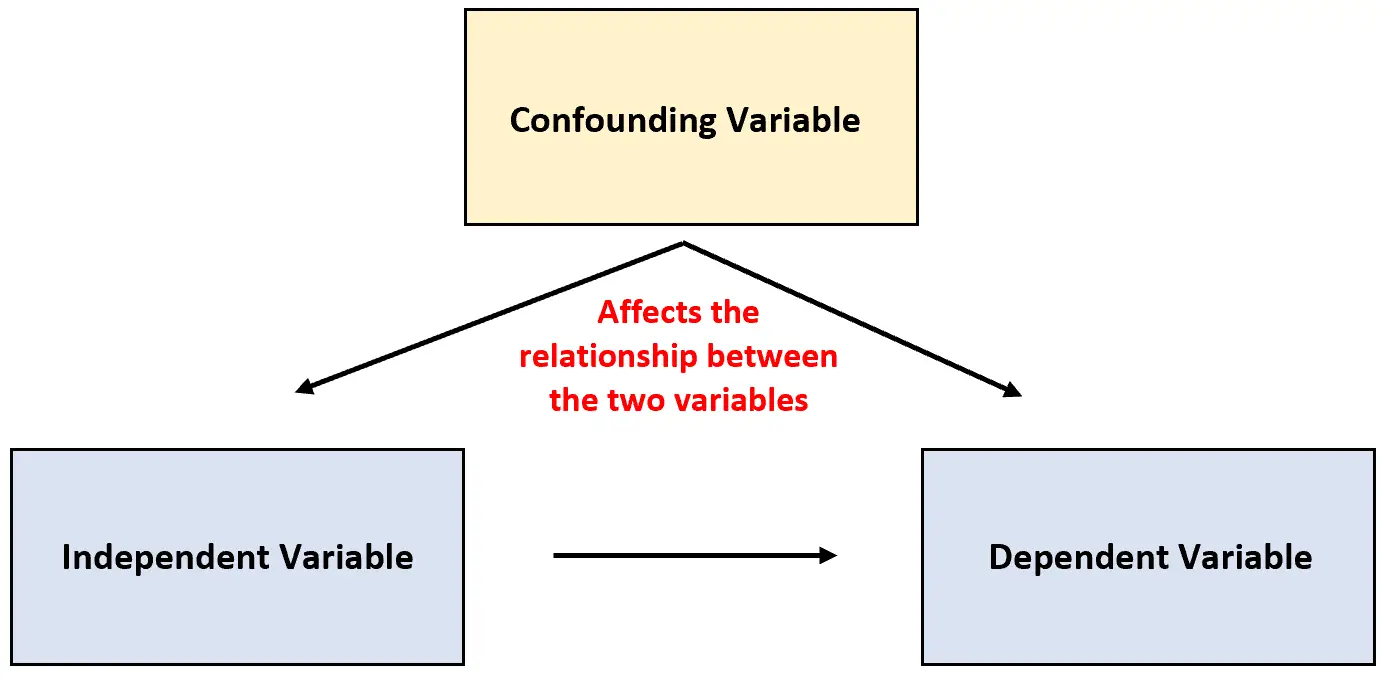
ตัวแปรประเภทนี้เรียกว่า ตัวแปรกวน และสามารถ สร้างความสับสนให้กับ ผลลัพธ์ของการศึกษาและทำให้ดูเหมือนว่ามีความสัมพันธ์ระหว่างสาเหตุและผลกระทบบางประเภทระหว่างตัวแปรสองตัวที่ไม่มีอยู่จริง

ตัวแปรที่ทำให้เกิดความสับสน: ตัวแปรที่ไม่รวมอยู่ในการทดสอบ แต่ส่งผลต่อความสัมพันธ์ระหว่างตัวแปรทั้งสองในการทดสอบ

ตัวแปรประเภทนี้อาจ ทำให้ ผลลัพธ์ของการทดสอบสับสนและนำไปสู่ผลลัพธ์ที่ไม่น่าเชื่อถือ

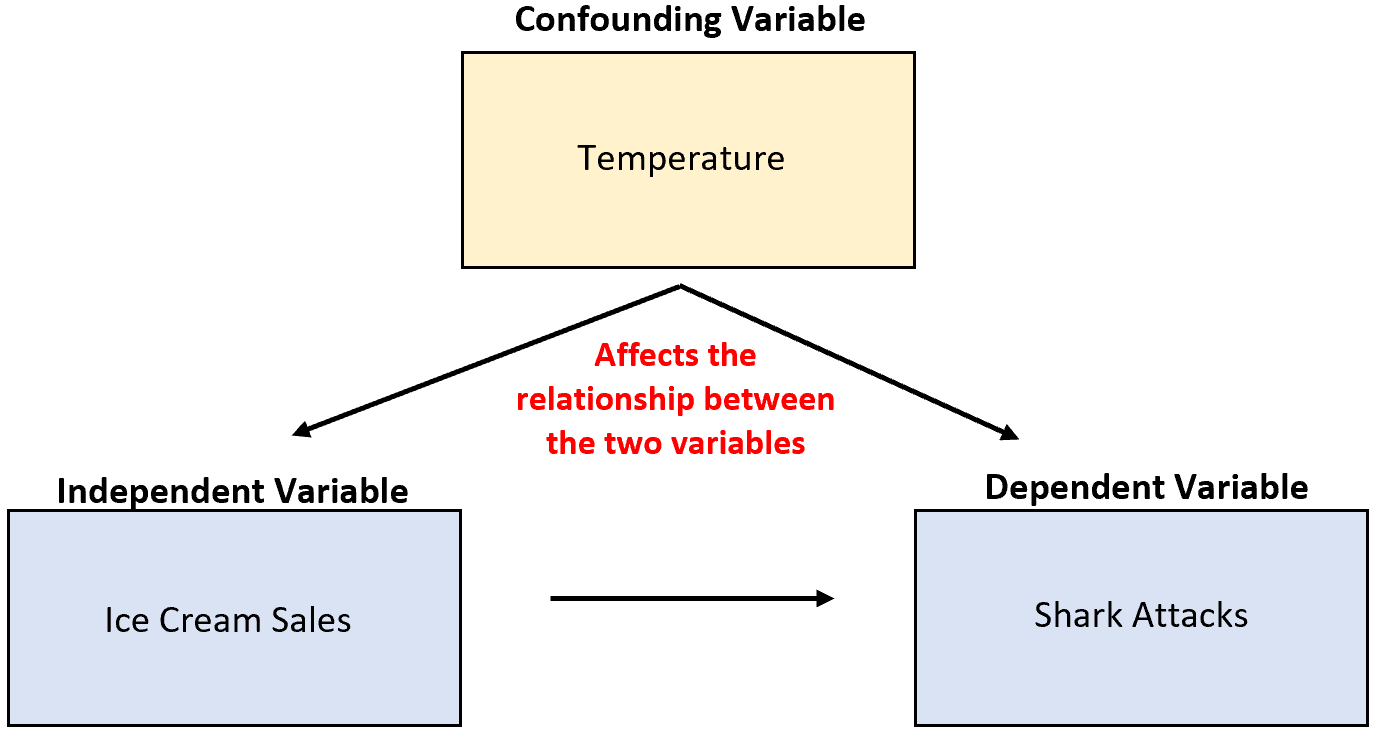
ตัวอย่างเช่น สมมติว่านักวิจัยรวบรวมข้อมูลเกี่ยวกับการขายไอศกรีมและการโจมตีของฉลาม และค้นพบว่าตัวแปรทั้งสองมีความสัมพันธ์กันสูง นี่หมายความว่ายอดขายไอศกรีมที่เพิ่มขึ้นทำให้ปลาฉลามโจมตีมากขึ้นใช่หรือไม่

มันไม่น่าเป็นไปได้ สาเหตุที่เป็นไปได้มากที่สุดคือ อุณหภูมิ ที่เปลี่ยนแปลงอย่างน่าสับสน เมื่ออากาศข้างนอกอุ่นขึ้น ผู้คนจะซื้อไอศกรีมมากขึ้น และผู้คนก็ไปทะเลมากขึ้น

ข้อกำหนดสำหรับตัวแปรที่ทำให้สับสน

เพื่อให้ตัวแปรเป็นตัวแปรที่น่าสับสน จะต้องเป็นไปตามข้อกำหนดต่อไปนี้:

1. จะต้องสัมพันธ์กับตัวแปรอิสระ

ในตัวอย่างก่อนหน้านี้ อุณหภูมิมีความสัมพันธ์กับตัวแปรอิสระของยอดขายไอศกรีม โดยเฉพาะอย่างยิ่งอุณหภูมิที่อุ่นขึ้นสัมพันธ์กับยอดขายไอศกรีมที่สูงขึ้น และอุณหภูมิที่เย็นลงพร้อมกับยอดขายที่ลดลง

2. ต้องมีความสัมพันธ์เชิงสาเหตุกับตัวแปรตาม

ในตัวอย่างก่อนหน้านี้ อุณหภูมิมีผลโดยตรงต่อจำนวนฉลามโจมตี โดยเฉพาะอย่างยิ่ง อุณหภูมิที่อุ่นขึ้นส่งผลให้ผู้คนลงสู่มหาสมุทรมากขึ้น ซึ่งเพิ่มโอกาสที่ฉลามจะโจมตีโดยตรง

เหตุใดตัวแปรที่ทำให้เกิดความสับสนจึงเป็นปัญหา

ตัวแปรที่สับสนเป็นปัญหาด้วยเหตุผลสองประการ:

1. ตัวแปรที่ทำให้เกิดความสับสนสามารถทำให้ปรากฏว่าความสัมพันธ์ระหว่างเหตุและผลมีอยู่ทั้งที่ความสัมพันธ์ไม่มีอยู่จริง

ในตัวอย่างก่อนหน้านี้ ตัวแปรอุณหภูมิที่น่าสับสนทำให้ดูเหมือนว่ามีความสัมพันธ์เชิงสาเหตุระหว่างการขายไอศกรีมกับการโจมตีของฉลาม

อย่างไรก็ตาม เรารู้ว่าการขายไอศกรีมไม่ได้ก่อให้เกิดการโจมตีจากฉลาม ตัวแปรอุณหภูมิที่น่าสับสนทำให้ดูเหมือนเป็นเช่นนั้น

2. ตัวแปรที่ทำให้เกิดความสับสนสามารถบดบังความสัมพันธ์ระหว่างสาเหตุและผลกระทบที่แท้จริงระหว่างตัวแปรได้

สมมติว่าเรากำลังศึกษาความสามารถในการออกกำลังกายเพื่อลดความดันโลหิต ตัวแปรที่กวนใจที่อาจเกิดขึ้นคือน้ำหนักเริ่มต้น ซึ่งมีความสัมพันธ์กับการออกกำลังกายและส่งผลโดยตรงต่อความดันโลหิต

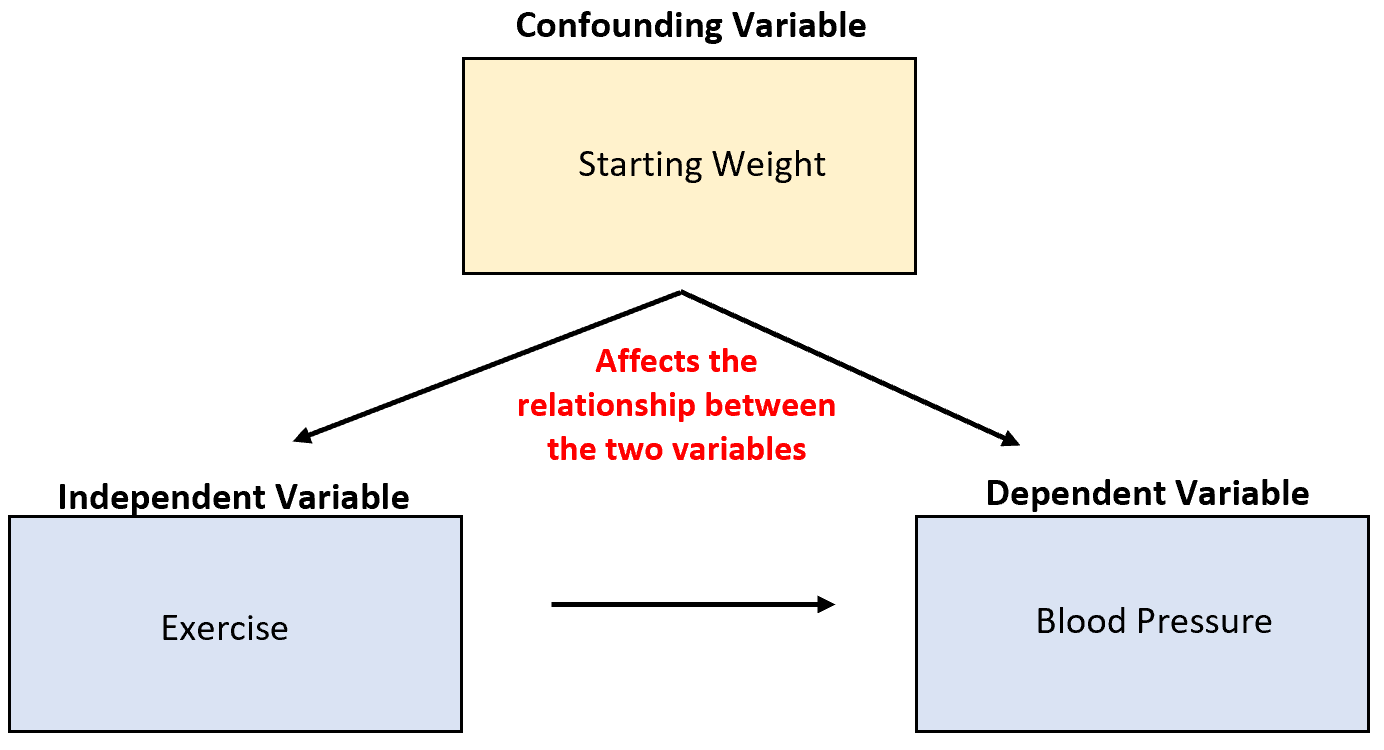
แม้ว่าการออกกำลังกายที่เพิ่มขึ้นอาจทำให้ความดันโลหิตลดลงได้ แต่น้ำหนักเริ่มต้นของแต่ละบุคคลก็มีผลกระทบอย่างมากต่อความสัมพันธ์ระหว่างตัวแปรทั้งสองนี้

ตัวแปรที่สับสนและความถูกต้องภายใน

ในแง่เทคนิค ตัวแปรที่ทำให้เกิดความสับสนส่งผลต่อ ความถูกต้องภายใน ของการศึกษา ซึ่งหมายถึงความถูกต้องของการระบุแหล่งที่มาของการเปลี่ยนแปลงใดๆ ในตัวแปรตามต่อการเปลี่ยนแปลงในตัวแปรอิสระ

เมื่อมีตัวแปรที่ทำให้เกิดความสับสน เราไม่สามารถพูดได้อย่างมั่นใจว่าการเปลี่ยนแปลงที่เราสังเกตในตัวแปรตามนั้นเป็นผลโดยตรงจากการเปลี่ยนแปลงในตัวแปรอิสระ

วิธีลดผลกระทบของตัวแปรที่ทำให้เกิดความสับสน

มีหลายวิธีในการลดผลกระทบของตัวแปรที่ทำให้เกิดความสับสน รวมถึงวิธีการต่อไปนี้:

1. การจัดสรรแบบสุ่ม

การสุ่มมอบหมาย หมายถึงกระบวนการสุ่มมอบหมายบุคคลในการศึกษาให้กับกลุ่มบำบัดหรือกลุ่มควบคุม

ตัวอย่างเช่น สมมติว่าเราต้องการศึกษาผลของยาเม็ดใหม่ต่อความดันโลหิต หากเรารับสมัครคน 100 คนเพื่อเข้าร่วมในการศึกษานี้ เราสามารถใช้เครื่องสร้างตัวเลขสุ่มเพื่อสุ่มกำหนดคน 50 คนให้กับกลุ่มควบคุม (ไม่มียาเม็ด) และ 50 คนไปยังกลุ่มการรักษา (ยาเม็ดใหม่)

ด้วยการใช้การสุ่ม เราจะเพิ่มโอกาสที่ทั้งสองกลุ่มจะมีลักษณะโดยประมาณที่คล้ายคลึงกัน ซึ่งหมายความว่าความแตกต่างใดๆ ที่สังเกตได้ระหว่างทั้งสองกลุ่มสามารถนำมาประกอบกับการรักษาได้

ซึ่งหมายความว่าการศึกษาต้องมี ความถูกต้องภายใน : สามารถระบุความแตกต่างใดๆ ของความดันโลหิตระหว่างกลุ่มกับตัวยาได้ เมื่อเทียบกับความแตกต่างระหว่างบุคคลในกลุ่ม

2. การปิดกั้น

การบล็อก หมายถึงการแบ่งบุคคลในการศึกษาออกเป็น “บล็อก” ตามค่าหนึ่งของตัวแปรที่ทำให้เกิดความสับสน เพื่อขจัดผลกระทบของตัวแปรที่ทำให้เกิดความสับสน

ตัวอย่างเช่น สมมติว่านักวิจัยต้องการเข้าใจผลของการรับประทานอาหารแบบใหม่ที่มีต่อการลดน้ำหนัก ตัวแปรอิสระคืออาหารแบบใหม่ และตัวแปรตามคือปริมาณน้ำหนักที่ลดลง

อย่างไรก็ตาม ตัวแปรที่น่าสับสนประการหนึ่งที่อาจทำให้เกิดการเปลี่ยนแปลงในการลดน้ำหนักคือ เพศ มีแนวโน้มว่าเพศของแต่ละบุคคลจะส่งผลต่อปริมาณน้ำหนักที่สูญเสียไป ไม่ว่าการรับประทานอาหารแบบใหม่จะได้ผลหรือไม่ก็ตาม

วิธีหนึ่งในการแก้ปัญหานี้คือการจัดแต่ละบุคคลให้เป็นหนึ่งในสองช่วงตึก:

• ชาย
• หญิง

จากนั้น ภายในแต่ละบล็อก เราจะสุ่มมอบหมายให้แต่ละบุคคลเข้ารับการรักษาอย่างใดอย่างหนึ่งจากสองวิธี:

• อาหารใหม่
• อาหารมาตรฐาน

การทำเช่นนี้ ความแปรผันภายในแต่ละช่วงตึกจะต่ำกว่าความแปรผันระหว่างบุคคลทั้งหมดอย่างมาก และเราจะสามารถเข้าใจได้ดีขึ้นว่าการรับประทานอาหารแบบใหม่ส่งผลต่อการลดน้ำหนักขณะควบคุมเพศอย่างไร

3. การโต้ตอบ

การออกแบบคู่ที่ตรงกัน คือประเภทของการออกแบบการทดลองที่เรา “จับคู่” บุคคลโดยพิจารณาจากค่าของตัวแปรที่อาจก่อให้เกิดความสับสน

ตัวอย่างเช่น สมมติว่านักวิจัยต้องการทราบว่าการรับประทานอาหารแบบใหม่ส่งผลต่อการลดน้ำหนักอย่างไรเมื่อเทียบกับการรับประทานอาหารมาตรฐาน ตัวแปรที่น่าสับสนสองประการในสถานการณ์นี้คือ อายุ และ เพศ

ในกรณีนี้ ให้รับสมัครนักวิจัย 100 วิชา จากนั้นจัดกลุ่มออกเป็น 50 คู่ตามอายุและเพศ ตัวอย่างเช่น:

• ชายอายุ 25 ปีจะถูกจับคู่กับชายอายุ 25 ปีอีกคน เนื่องจากพวกเขา “เข้ากัน” ในแง่ของอายุและเพศ
• ผู้หญิงอายุ 30 ปีจะถูกจับคู่กับผู้หญิงอายุ 30 ปีอีกคนหนึ่ง เนื่องจากพวกเขายังจับคู่กันในแง่ของอายุและเพศ ฯลฯ

จากนั้นในแต่ละคู่ อาสาสมัครหนึ่งคนจะถูกสุ่มให้ติดตามอาหารใหม่เป็นเวลา 30 วัน และอีกคนหนึ่งจะถูกมอบหมายให้ติดตามอาหารมาตรฐานเป็นเวลา 30 วัน

เมื่อครบ 30 วัน ผู้วิจัยจะวัดน้ำหนักที่ลดลงทั้งหมดสำหรับแต่ละวิชา

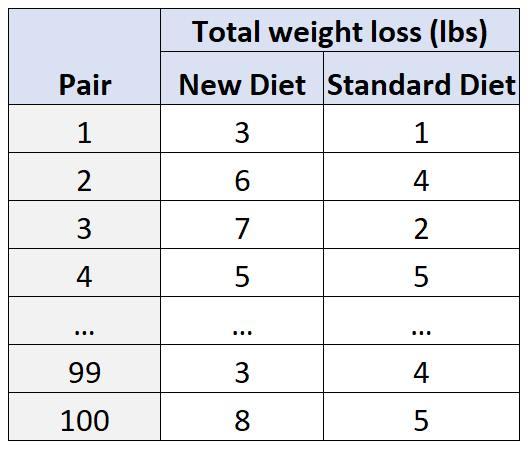
การใช้การออกแบบประเภทนี้ นักวิจัยสามารถมั่นใจได้ว่าความแตกต่างใดๆ ในการลดน้ำหนักนั้นอาจเป็นผลมาจากประเภทของอาหารที่ใช้ มากกว่าตัวแปรที่สับสนระหว่าง อายุ และ เพศ

การออกแบบประเภทนี้มีข้อเสียบางประการ ได้แก่:

1. เสียวิชาสองวิชาหากวิชาใดวิชาหนึ่งหลุดออกไป หากผู้เข้าร่วมตัดสินใจลาออกจากการศึกษา คุณจะสูญเสียวิชาสองวิชาเนื่องจากคุณไม่มีคู่ที่สมบูรณ์อีกต่อไป

2. ต้องใช้เวลาในการค้นหาการแข่งขัน การค้นหาหัวข้อที่ตรงกับตัวแปรบางอย่าง เช่น เพศและอายุ อาจใช้เวลานาน

3. ไม่สามารถจับคู่หัวข้อได้อย่างสมบูรณ์ ไม่ว่าคุณจะพยายามแค่ไหน ก็มักจะมีความแปรผันในแต่ละคู่เสมอ

อย่างไรก็ตาม หากการศึกษามีทรัพยากรเพียงพอที่จะนำการออกแบบนี้ไปใช้ การศึกษาจะมีประสิทธิภาพมากในการกำจัดผลกระทบของตัวแปรที่สับสน