ตัวแปรเชิงคุณภาพและเชิงปริมาณ: อะไรคือความแตกต่าง?

ในทางสถิติ มีตัวแปรอยู่ 2 ประเภท คือ

1. ตัวแปรเชิงปริมาณ: บางครั้งเรียกว่าตัวแปร “ตัวเลข” ซึ่งเป็นตัวแปรที่แสดงถึงปริมาณที่วัดได้ ตัวอย่างได้แก่:

• จำนวนนักเรียนในชั้นเรียน
• จำนวนตารางฟุตในบ้าน
• ขนาดประชากรของเมือง
• อายุของแต่ละบุคคล
• ขนาดของแต่ละบุคคล

2. ตัวแปรเชิงคุณภาพ: บางครั้งเรียกว่าตัวแปร “หมวดหมู่” ซึ่งเป็นตัวแปรที่ใช้ชื่อหรือป้ายกำกับและสามารถจัดเป็นหมวดหมู่ได้ ตัวอย่างได้แก่:

• สีตา (เช่น “สีฟ้า”, “สีเขียว”, “สีน้ำตาล”)
• เพศ (เช่น “ผู้ชาย” “ผู้หญิง”)
• พันธุ์สุนัข (เช่น “แล็บ”, “บูลด็อก”, “พุดเดิ้ล”)
• ระดับการศึกษา (เช่น “มัธยมปลาย” “อนุปริญญา” “ปริญญาตรี”)
• สถานภาพการสมรส (เช่น “แต่งงานแล้ว” “โสด” “หย่าร้าง”)

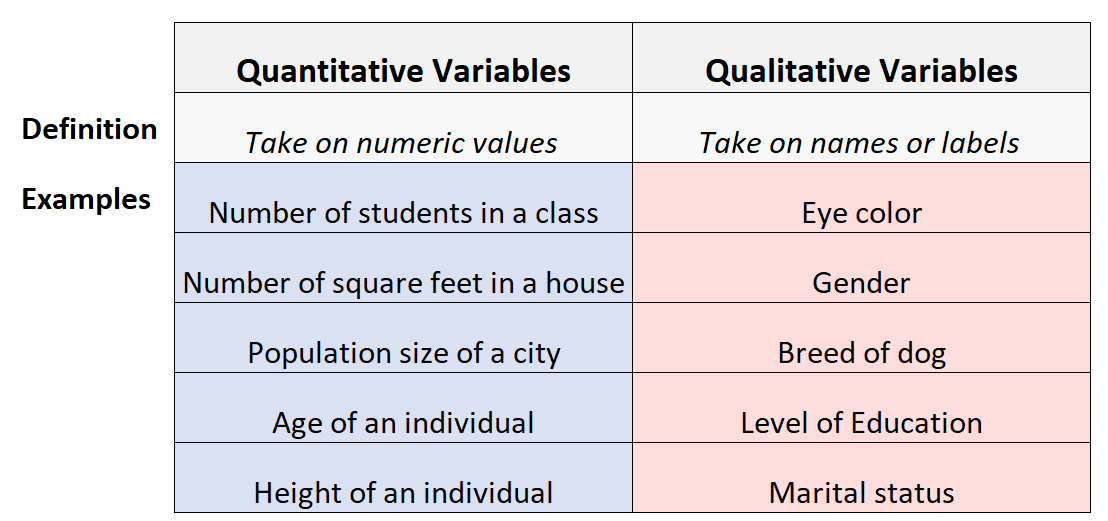
ตัวแปรทุกตัวที่คุณจะพบในสถิติสามารถจำแนกได้เป็นเชิงปริมาณหรือเชิงคุณภาพ

ตัวอย่าง: การจำแนกประเภทของตัวแปรเชิงปริมาณและเชิงคุณภาพ

พิจารณาชุดข้อมูลต่อไปนี้ที่มีข้อมูลเกี่ยวกับผู้เล่นบาสเก็ตบอล 10 คน:

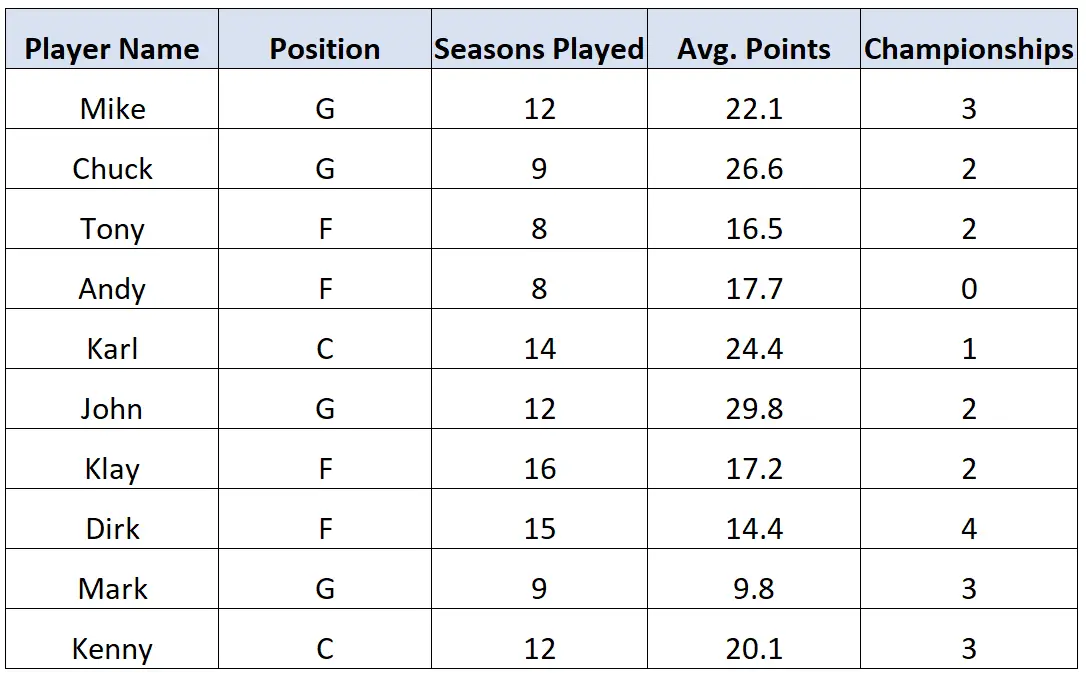
ชุดข้อมูลนี้มีตัวแปรทั้งหมดห้าตัวแปร สองในนั้นเป็นตัวแปรเชิงคุณภาพและสามในนั้นเป็นตัวแปรเชิงปริมาณ:

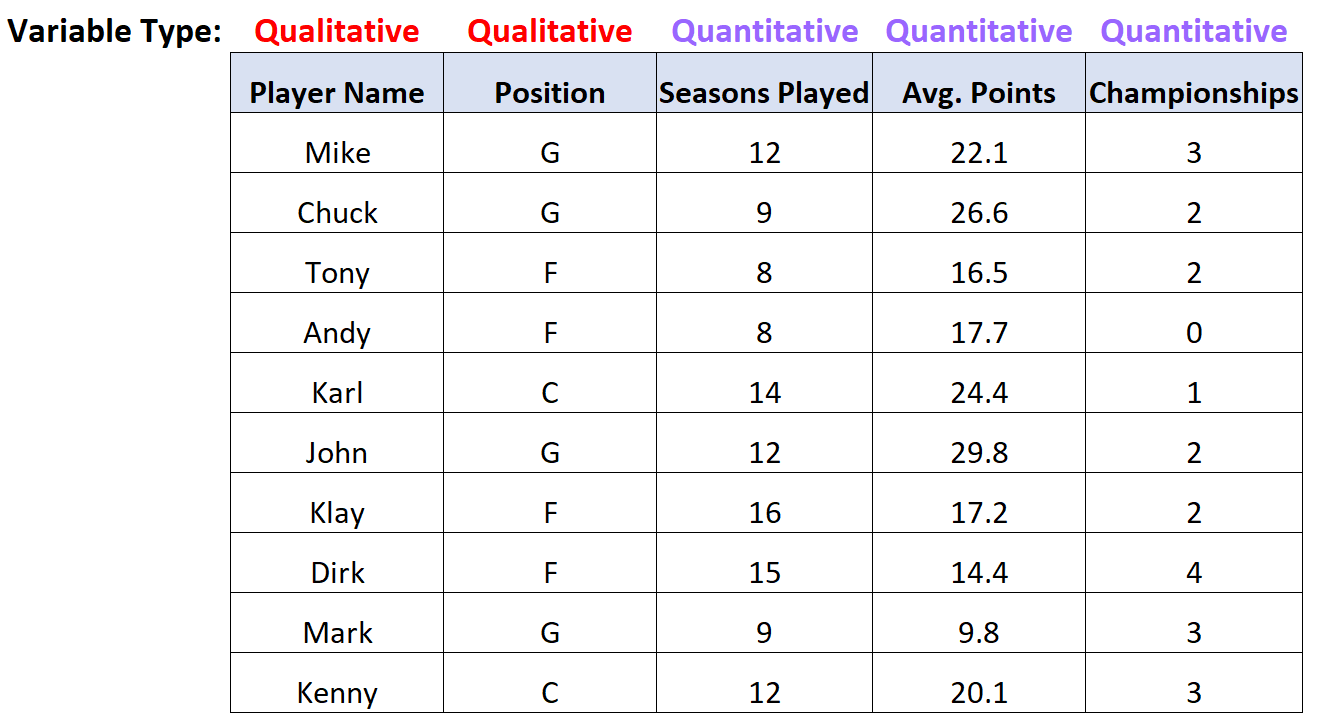
สรุปตัวแปรเชิงปริมาณและเชิงคุณภาพ

เราสามารถใช้มาตรการต่างๆ มากมายเพื่อสรุป ตัวแปรเชิงปริมาณ ได้แก่:

• การวัดแนวโน้มจากศูนย์กลาง เช่น ค่าเฉลี่ย ค่ามัธยฐาน และโหมด
• การวัดการกระจายตัว เช่น พิสัย พิสัยระหว่างควอไทล์ และส่วนเบี่ยงเบนมาตรฐาน

อย่างไรก็ตาม เราสามารถใช้เฉพาะตารางความถี่และตารางความถี่สัมพัทธ์ในการสรุป ตัวแปรเชิงคุณภาพ เท่านั้น

เพื่ออธิบายสิ่งนี้ ให้พิจารณาชุดข้อมูลจากตัวอย่างก่อนหน้านี้อีกครั้ง:

สำหรับตัวแปรเชิงปริมาณ ที่เล่นในฤดูกาล เราสามารถคำนวณตัวชี้วัดต่อไปนี้:

• เฉลี่ย: 11.5
• ค่ามัธยฐาน: 12
• โหมด: 12
• ช่วง: 8
• สเกลระหว่างควอไทล์: 4.5
• ส่วนเบี่ยงเบนมาตรฐาน: 2.915

ตัวชี้วัดเหล่านี้ทำให้เรามีความคิดที่ดีว่าค่ากลางอยู่ที่ใดรวมถึงการแจกแจงค่าของตัวแปรนั้น

และสำหรับ ตำแหน่ง ตัวแปรเชิงคุณภาพ เราสามารถสร้างตารางความถี่เพื่ออธิบายว่าค่าต่างๆ ปรากฏบ่อยเพียงใด:

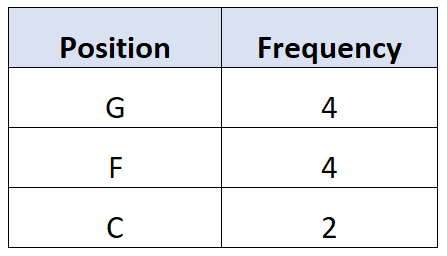
ตารางนี้ช่วยให้เราเห็นได้อย่างรวดเร็วว่าแต่ละตำแหน่ง (L=guard, F=forward, C=center) เกิดขึ้นในชุดข้อมูลบ่อยแค่ไหน

แหล่งข้อมูลเพิ่มเติม

สถิติเชิงพรรณนาหรือเชิงอนุมาน
สถิติเทียบกับพารามิเตอร์
ระดับการวัด: ระบุ ลำดับ ช่วงเวลา และอัตราส่วน