วิธีใช้ invnorm บนเครื่องคิดเลข ti-84 (พร้อมตัวอย่าง)

คุณสามารถใช้ฟังก์ชัน invNorm() บนเครื่องคิดเลข TI-84 เพื่อค้นหาค่าวิกฤต z ที่สัมพันธ์กับ การแจกแจงแบบปกติ

ฟังก์ชันนี้ใช้ไวยากรณ์ต่อไปนี้:

invNorm(ความน่าจะเป็น, μ, σ)

ทอง:

• ความน่าจะเป็น: ระดับนัยสำคัญ
• μ: ค่าเฉลี่ยประชากร
• σ: ส่วนเบี่ยงเบนมาตรฐานประชากร

คุณสามารถเข้าถึงฟังก์ชันนี้บนเครื่องคิดเลข TI-84 ได้โดยกด 2 จากนั้นกด VARS สิ่งนี้จะนำคุณไปยังหน้าจอ DISTR ซึ่งคุณสามารถใช้ invNorm() :

ตัวอย่างต่อไปนี้แสดงวิธีใช้ฟังก์ชันนี้ในทางปฏิบัติ

ตัวอย่างที่ 1: ค่าวิกฤต Z สำหรับการทดสอบด้านเดียว

สมมติว่านักวิจัยทำการทดสอบสมมติฐานทางมือซ้ายโดยใช้ α = 0.05 ค่าวิกฤต z ที่สอดคล้องกับระดับอัลฟ่านี้คืออะไร?

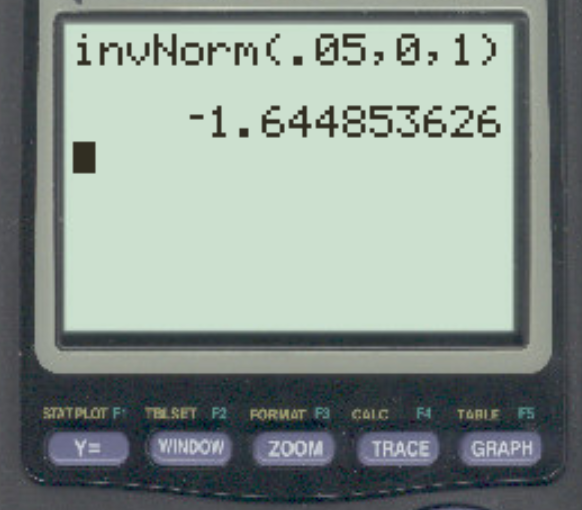
คำตอบคือ z = -1.64485

สมมติว่านักวิจัยทำการทดสอบสมมติฐานแบบตรงโดยใช้ α = 0.05 ค่าวิกฤต z ที่สอดคล้องกับระดับอัลฟ่านี้คืออะไร?

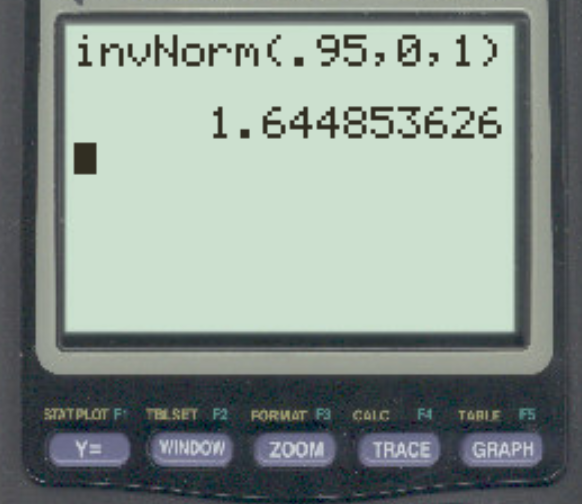
คำตอบคือ z = 1.64485

ตัวอย่างที่ 2: ค่าวิกฤต Z สำหรับการทดสอบสองด้าน

สมมติว่านักวิจัยทำการทดสอบสมมติฐานแบบสองด้านโดยใช้ α = 0.05 ค่าวิกฤต z ที่สอดคล้องกับระดับอัลฟ่านี้คืออะไร?

ในการหาค่าวิกฤตนี้ เราสามารถใช้สูตร 1 – α/2 ได้ ในกรณีนี้ เราจะใช้ 1 – 0.05/2 = 0.975 สำหรับความน่าจะเป็น:

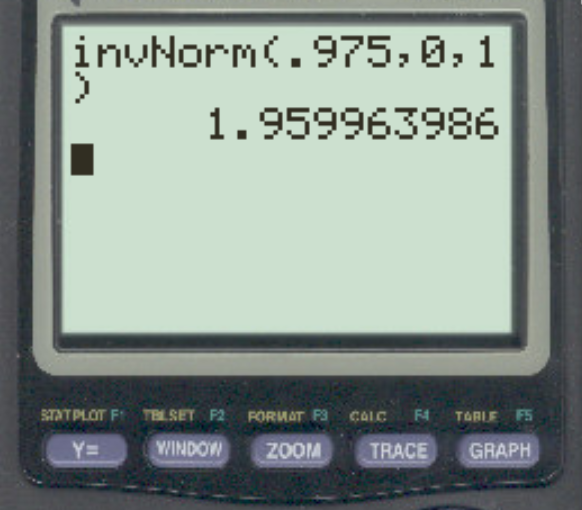
คำตอบคือ z = 1.96 .

ตัวอย่างที่ 3: ค่าวิกฤต Z สำหรับคะแนนจุดตัด

สมมติว่าคะแนนในการสอบรายการใดรายการหนึ่งมีการแจกแจงตามปกติโดยมีค่าเฉลี่ย 70 และส่วนเบี่ยงเบนมาตรฐาน 8 คะแนนใดที่แยกคะแนน 10% แรกออกจากส่วนที่เหลือ

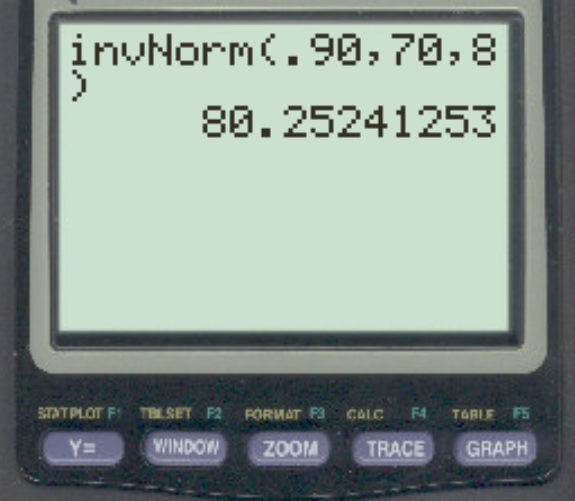
คำตอบคือ 80.25 .

สมมติว่าความสูงของผู้ชายในเมืองใดเมืองหนึ่งโดยปกติจะแจกแจงโดยมีค่าเฉลี่ย 68 นิ้ว และส่วนเบี่ยงเบนมาตรฐาน 4 นิ้ว สูงแค่ไหนที่แยกส่วนล่าง 25% จากส่วนที่เหลือ?

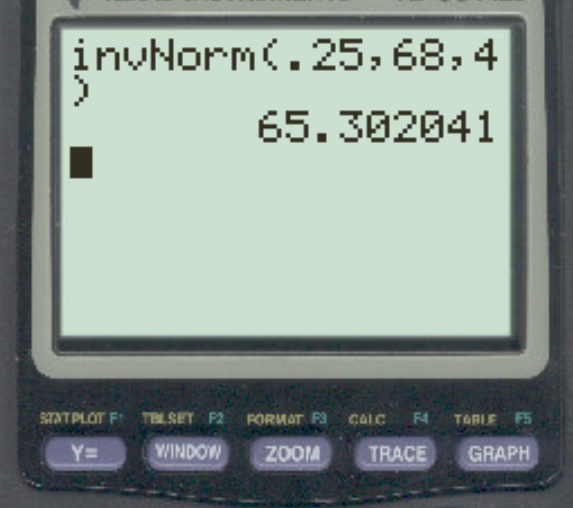
คำตอบคือ 65.3 นิ้ว

แหล่งข้อมูลเพิ่มเติม

วิธีการคำนวณความน่าจะเป็นแบบทวินามบนเครื่องคิดเลข TI-84
วิธีการคำนวณความน่าจะเป็นปัวซองบนเครื่องคิดเลข TI-84
วิธีการคำนวณความน่าจะเป็นทางเรขาคณิตบนเครื่องคิดเลข TI-84