พล็อต bland-altman คืออะไร? (คำจำกัดความ & #038; ตัวอย่าง)
พล็อต Bland-Altman ถูกใช้เพื่อแสดงภาพความแตกต่างในการวัดระหว่างเครื่องมือสองชนิดที่แตกต่างกันหรือสองเทคนิคการวัดที่แตกต่างกัน
มักใช้เพื่อประเมินความคล้ายคลึงกันของเครื่องมือหรือเทคนิคใหม่ในการวัดบางสิ่งกับเครื่องมือหรือเทคนิคที่ใช้อยู่ในปัจจุบัน
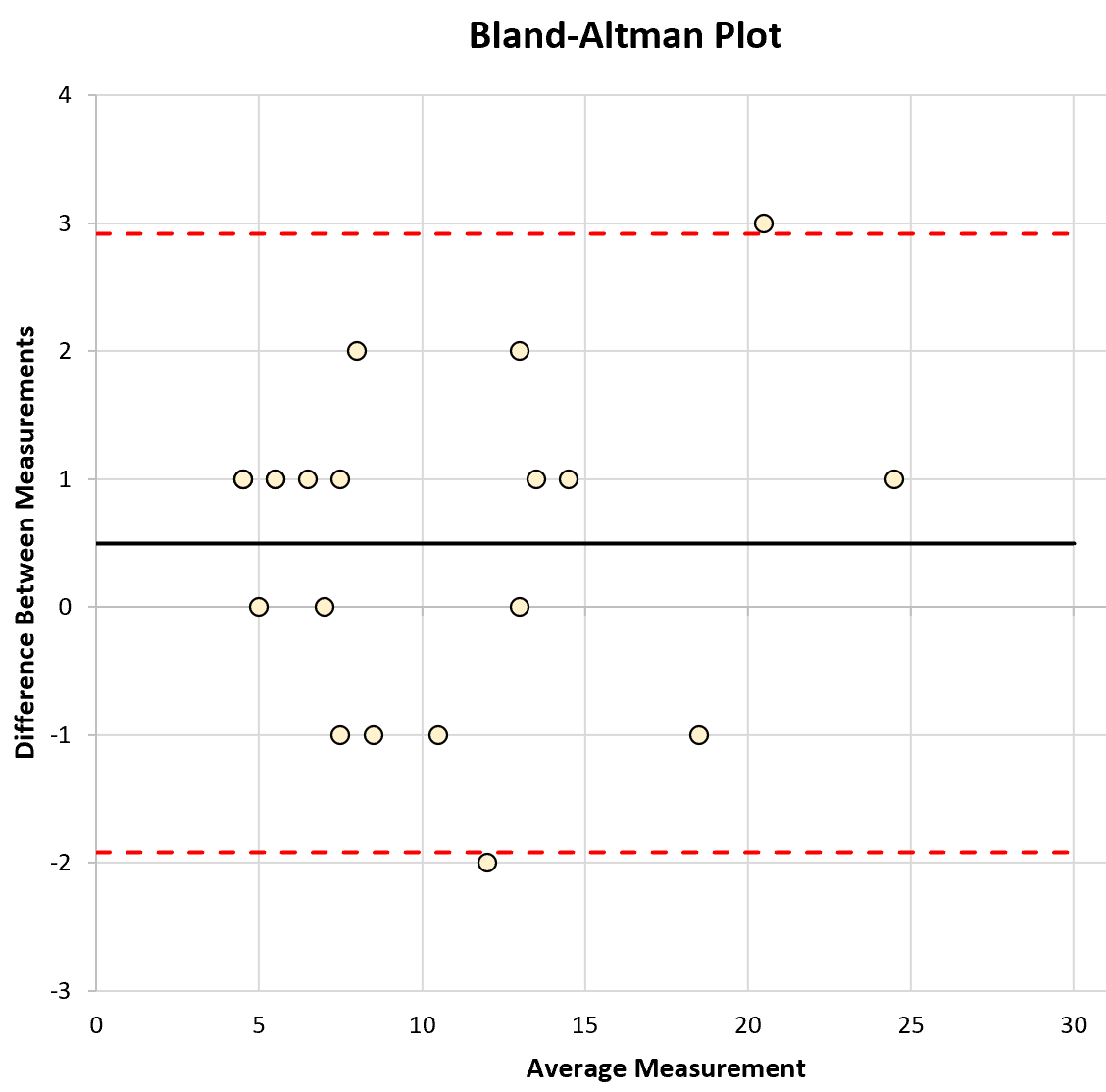
แกน x ของกราฟจะแสดงการวัดเฉลี่ยของเครื่องมือทั้งสอง และแกน y จะแสดงความแตกต่างในการวัดระหว่างเครื่องมือทั้งสอง
สามบรรทัดต่อไปนี้จะแสดงอยู่ในโครงเรื่องด้วย:
- ความแตกต่างโดยเฉลี่ยในการวัดระหว่างเครื่องมือทั้งสอง
- ขีดจำกัดบนของช่วงความเชื่อมั่น 95% สำหรับผลต่างเฉลี่ย
- ขีดจำกัดล่างของช่วงความเชื่อมั่น 95% สำหรับผลต่างเฉลี่ย
โครงเรื่องประเภทนี้มีประโยชน์ในการพิจารณาสองสิ่ง:
1. อะไรคือความแตกต่างโดยเฉลี่ยในการวัดระหว่างเครื่องมือทั้งสอง?
เส้นแนวนอนที่ลากตรงกลางกราฟแสดงความแตกต่างโดยเฉลี่ยในการวัดระหว่างเครื่องมือทั้งสอง ค่านี้มักเรียกว่า “อคติ” ระหว่างเครื่องมือต่างๆ
ยิ่งค่านี้อยู่ห่างจากศูนย์มากเท่าไร ความต่างโดยเฉลี่ยในการวัดระหว่างเครื่องมือก็จะยิ่งมากขึ้นเท่านั้น
2. ช่วงทั่วไปของข้อตกลงระหว่างตราสารทั้งสองคืออะไร?
เส้นช่วงความเชื่อมั่นด้านบนและด้านล่างทำให้เราเข้าใจถึงช่วงทั่วไปของข้อตกลงระหว่างเครื่องมือทั้งสอง โดยทั่วไปแล้ว 95% ของความแตกต่างระหว่างตราสารทั้งสองจะอยู่ภายในขีดจำกัดความเชื่อมั่นเหล่านี้
ยิ่งช่วงความเชื่อมั่นกว้างขึ้น ช่วงของความแตกต่างในการวัดระหว่างเครื่องมือทั้งสองก็จะยิ่งกว้างขึ้น
ตัวอย่างทีละขั้นตอนต่อไปนี้แสดงวิธีสร้างและตีความพล็อตเรื่อง Bland-Altman ตั้งแต่เริ่มต้น
หมายเหตุ: พล็อต Bland-Altman บางครั้งเรียกว่า Tukey พล็อตผลต่างค่าเฉลี่ย ชื่อเหล่านี้ใช้แทนกันได้
ขั้นตอนที่ 1: รวบรวมข้อมูล
สมมติว่านักชีววิทยาต้องการทราบว่าเครื่องมือสองชนิดที่แตกต่างกันนี้ใช้ในการวัดน้ำหนักของกบในหน่วยกรัมมีความคล้ายคลึงกันอย่างไร เขาใช้เครื่องมือสองตัว (A และ B) เพื่อชั่งน้ำหนักกบ 20 ตัวชุดเดียวกัน
น้ำหนักของกบซึ่งวัดโดยเครื่องดนตรีแต่ละชนิดแสดงไว้ในตารางต่อไปนี้:
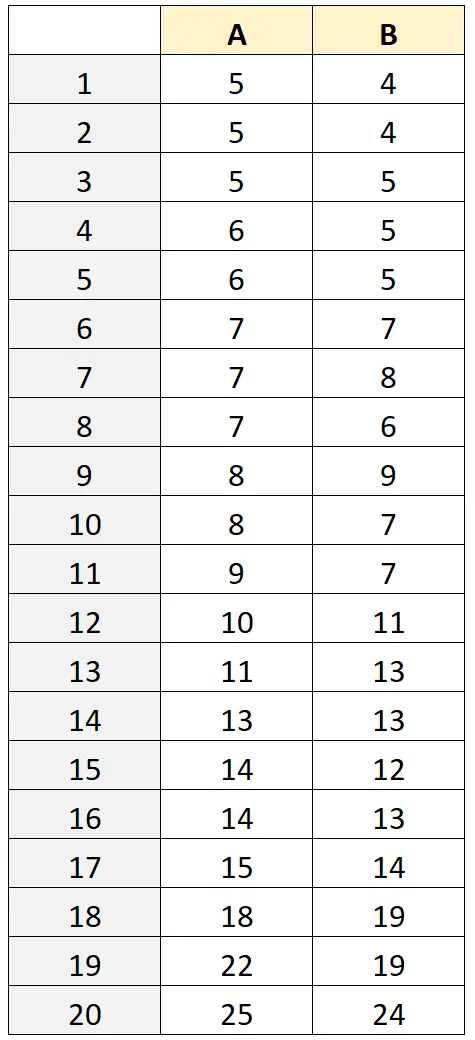
ขั้นตอนที่ 2: คำนวณการวัดโดยเฉลี่ยและผลต่างของการวัด
ต่อไป เราจะคำนวณค่าเฉลี่ยที่วัดได้ ((A+B)/2) และผลต่างในการวัด (AB) ของกบแต่ละตัว:
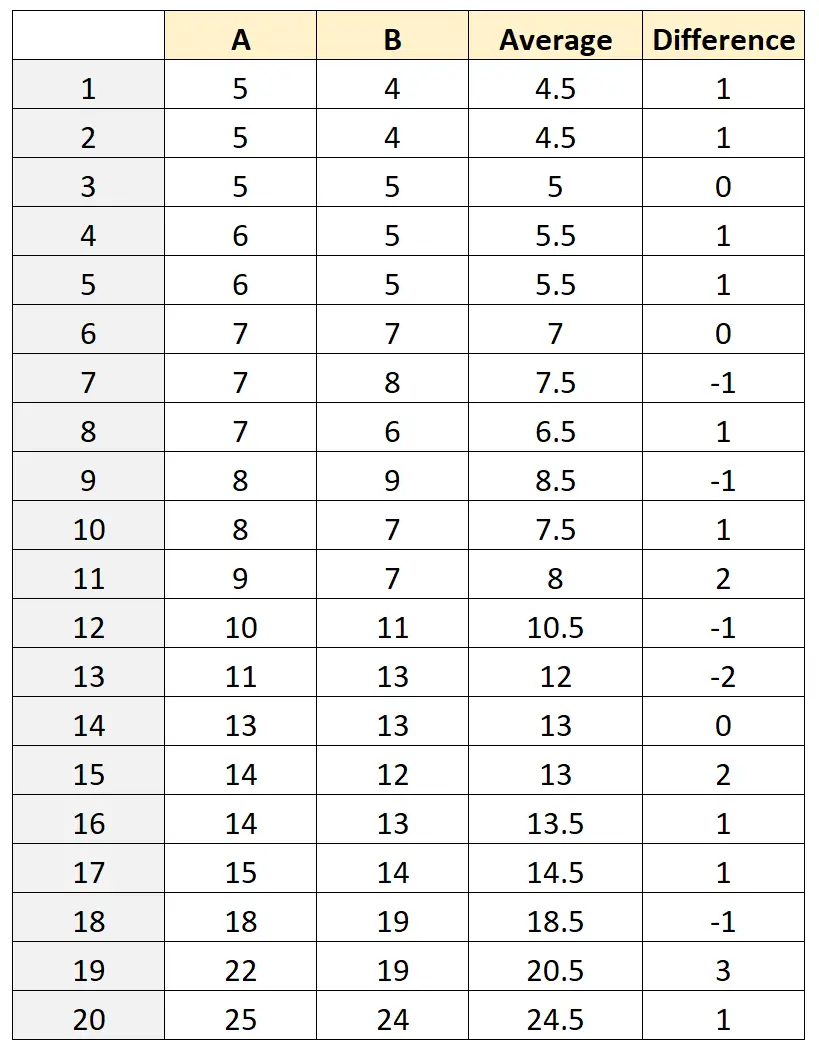
ขั้นตอนที่ 3: คำนวณผลต่างเฉลี่ยและช่วงความเชื่อมั่น
ค่าเฉลี่ยของค่าในคอลัมน์ ส่วนต่าง กลายเป็น 0.5 .
ค่าเบี่ยงเบนมาตรฐานของค่าในคอลัมน์ ความแตกต่าง กลายเป็น 1.235 .
ขีดจำกัดบนและล่างของช่วงความเชื่อมั่นสำหรับผลต่างเฉลี่ยสามารถคำนวณได้ดังนี้:
ขีดจำกัดบน: x + 1.96*s = 0.5 + 1.96*1.235 = 2.92
ขีดจำกัดล่าง: x – 1.96*s = 0.5 – 1.96*1.235 = -1.92
ต่อไปนี้เป็นวิธีการตีความค่าเหล่านี้:
- โดยเฉลี่ยแล้ว เครื่องดนตรี A มีน้ำหนักมากกว่าเครื่องดนตรี B 0.5 กรัม
- 95% ของน้ำหนักที่แตกต่างกันระหว่างเครื่องดนตรีทั้งสองควรอยู่ระหว่าง -1.92 กรัมถึง 2.92 กรัม
ต่อไป เราจะสร้างพล็อตเรื่อง Bland-Altman เพื่อให้เห็นภาพค่าเหล่านี้
ขั้นตอนที่ 4: สร้างพล็อต
จากนั้นเราสามารถสร้างแผนภาพต่อไปนี้ซึ่งแสดงการวัดเฉลี่ยของเครื่องมือทั้งสองบนแกน x และความแตกต่างระหว่างการวัดบนแกน y
นอกจากนี้เรายังสามารถเพิ่มเส้นแนวนอนให้กับความแตกต่างโดยเฉลี่ยระหว่างการวัด (0.5) รวมถึงขีดจำกัดความเชื่อมั่นด้านบน (2.92) และขีดจำกัดความเชื่อมั่นด้านล่าง (-1.92) ที่เราคำนวณในขั้นตอนก่อนหน้า:

แหล่งข้อมูลเพิ่มเติม
วิธีสร้างพล็อตเรื่อง Bland-Altman ใน Excel
วิธีสร้างพล็อต Bland-Altman ใน R
วิธีสร้างพล็อตเรื่อง Bland-Altman ใน Python