คู่มือฉบับสมบูรณ์: วิธีตีความผลลัพธ์ anova ใน excel

การวิเคราะห์ความแปรปรวนแบบทางเดียว ใช้เพื่อพิจารณาว่ามีความแตกต่างที่มีนัยสำคัญทางสถิติระหว่างค่าเฉลี่ยของกลุ่มอิสระสามกลุ่มขึ้นไปหรือไม่

ตัวอย่างต่อไปนี้ให้คำแนะนำฉบับสมบูรณ์เกี่ยวกับวิธีตีความผลลัพธ์ของการวิเคราะห์ความแปรปรวนแบบทางเดียวใน Excel

ตัวอย่าง: วิธีตีความผลลัพธ์ ANOVA ใน Excel

สมมติว่าครู สุ่มให้ นักเรียน 30 คนในชั้นเรียนใช้วิธีเรียนแบบใดแบบหนึ่งจากสามวิธีเพื่อเตรียมตัวสอบ

ภาพหน้าจอต่อไปนี้แสดงคะแนนของนักเรียนตามวิธีที่พวกเขาใช้:

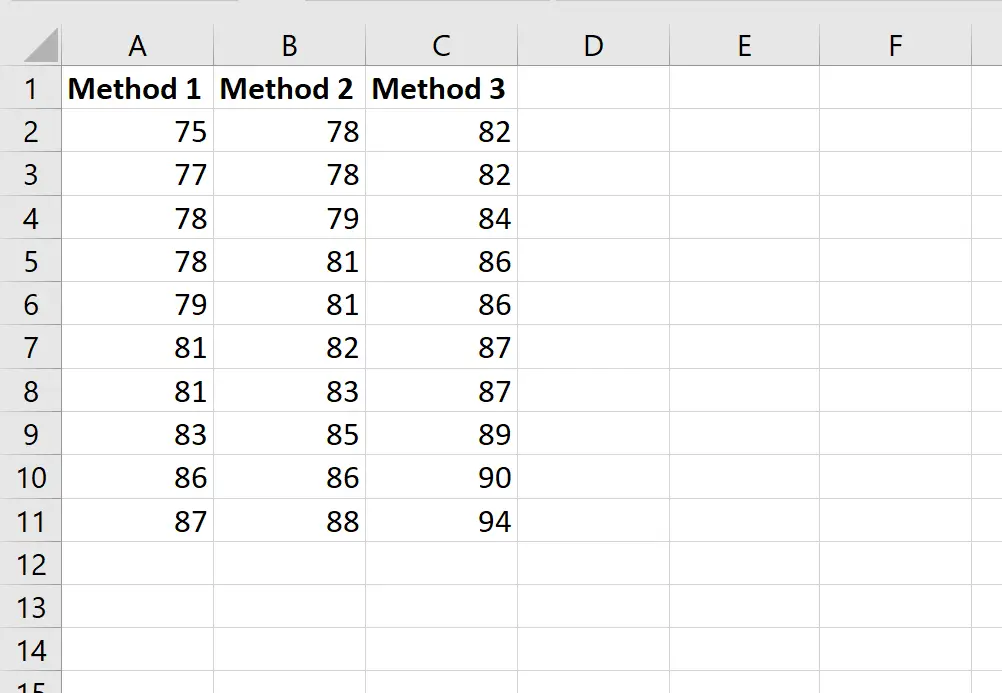
สมมติว่าครูต้องการทำการวิเคราะห์ความแปรปรวนแบบทางเดียวเพื่อพิจารณาว่าคะแนนเฉลี่ยของทั้ง 3 กลุ่มเท่ากันหรือไม่

เมื่อต้องการดำเนินการวิเคราะห์ความแปรปรวนแบบทางเดียวใน Excel ให้คลิกแท็บ ข้อมูล บน Ribbon ด้านบน จากนั้นคลิก การวิเคราะห์ข้อมูล ในกลุ่ม วิเคราะห์

หากคุณไม่เห็นตัวเลือก การวิเคราะห์ข้อมูล คุณ ต้อง โหลดซอฟต์แวร์ Analysis ToolPak ฟรีก่อน

เมื่อคุณคลิกแล้ว หน้าต่างใหม่จะปรากฏขึ้น เลือก Anova: Single Factor แล้วคลิก ตกลง

ในหน้าต่างใหม่ที่ปรากฏขึ้น ให้ป้อนข้อมูลต่อไปนี้:

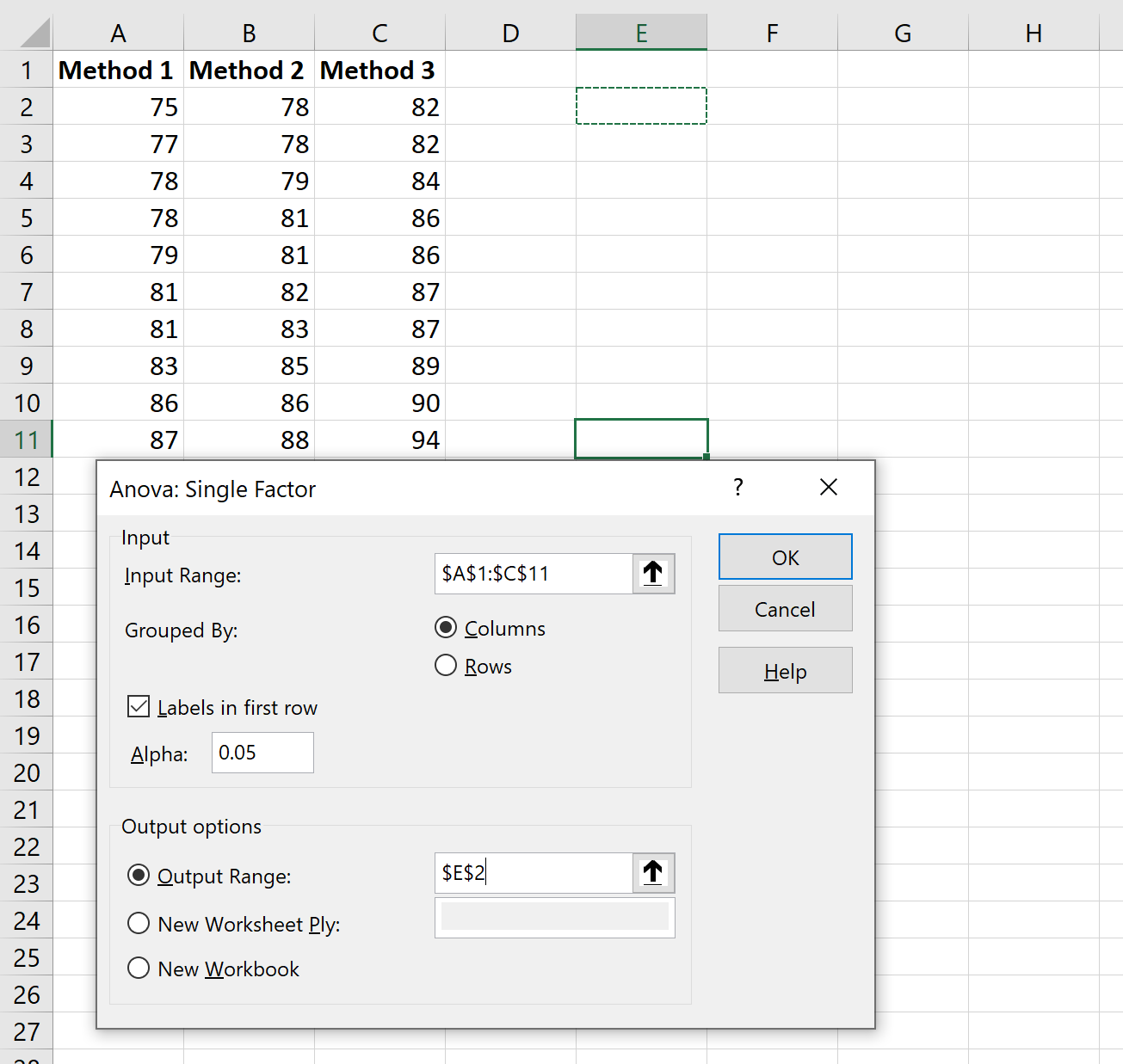
เมื่อคุณคลิก ตกลง ผลลัพธ์ ANOVA แบบทางเดียวจะปรากฏขึ้น:

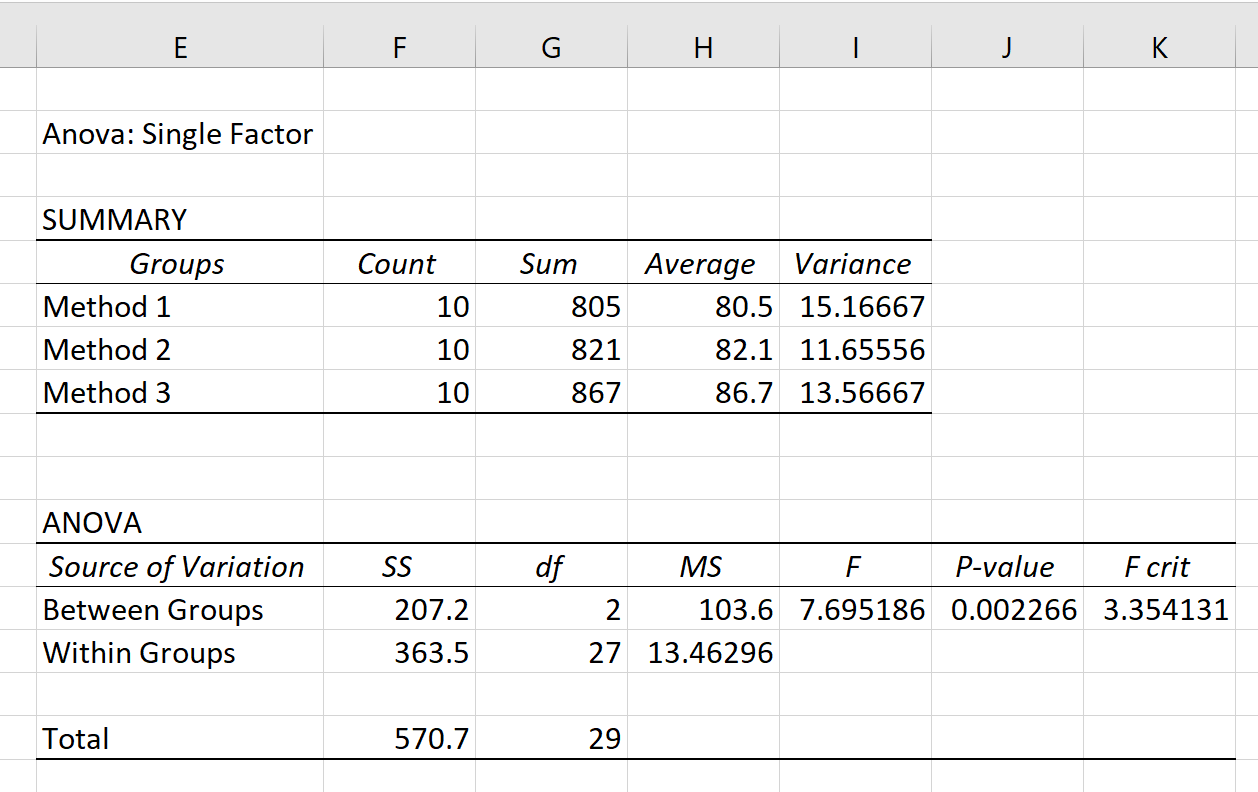
ผลลัพธ์จะแสดงสองตาราง: SUMMARY และ ANOVA

ต่อไปนี้เป็นวิธีตีความค่าในแต่ละตาราง:

ตารางสรุป :

• กลุ่ม : ชื่อกลุ่ม
• Count : จำนวน การสังเกต ในแต่ละกลุ่ม
• Sum : ผลรวมของค่าแต่ละกลุ่ม
• ค่าเฉลี่ย : ค่าเฉลี่ยในแต่ละกลุ่ม
• ความแปรปรวน : ความแปรปรวนของค่าในแต่ละกลุ่ม

ตารางนี้ให้ข้อมูลสถิติสรุปที่เป็นประโยชน์หลายประการสำหรับแต่ละกลุ่มที่ใช้ใน ANOVA

จากตารางนี้ เราจะเห็นว่านักเรียนที่ใช้วิธีที่ 3 มีคะแนนสอบเฉลี่ยสูงสุด (86.7) แต่ยังมีคะแนนสอบ แปรปรวน สูงสุดอีกด้วย บทวิจารณ์ (13.56667)

หากต้องการทราบว่าความแตกต่างในค่าเฉลี่ยกลุ่มมีนัยสำคัญทางสถิติหรือไม่ เราต้องอ้างอิงตาราง ANOVA

ตารางการวิเคราะห์ความแปรปรวน :

• แหล่งที่มาของการเปลี่ยนแปลง : ความแปรผันที่วัดได้ (ระหว่างกลุ่มหรือภายในกลุ่ม)
• SS : ผลรวมของกำลังสองสำหรับแหล่งที่มาของการเปลี่ยนแปลงแต่ละแหล่ง
• df : องศาความเป็นอิสระ คำนวณเป็น #groups-1 สำหรับ df Between และ #observations – #groups สำหรับ df Within
• MS : ผลรวมเฉลี่ยของกำลังสอง คำนวณเป็น SS/df
• F : ค่า F โดยรวม คำนวณเป็น MS Between / MS Within
• P-value : ค่า p ที่สอดคล้องกับค่า F โดยรวม
• F crit : ค่าวิกฤต F ซึ่งสอดคล้องกับ α = 0.05

ค่าที่สำคัญที่สุดในตารางนี้คือ ค่า p ซึ่งกลายเป็น 0.002266

โปรดจำไว้ว่าการวิเคราะห์ความแปรปรวนทางเดียวใช้สมมติฐานว่างและทางเลือกต่อไปนี้:

• H ₀ : ค่าเฉลี่ยกลุ่มทั้งหมดเท่ากัน
• _HA : ค่าเฉลี่ยของกลุ่มไม่เท่ากันทั้งหมด

เนื่องจากค่า p น้อยกว่า α = 0.05 เราจึงปฏิเสธสมมติฐานว่างของการวิเคราะห์ความแปรปรวนแบบทางเดียว และสรุปได้ว่าเรามีหลักฐานเพียงพอที่จะระบุว่าค่าเฉลี่ยกลุ่มทั้งหมดไม่เท่ากัน

ซึ่งหมายความว่าวิธีการศึกษาทั้งสามวิธีไม่ได้ทำให้คะแนนสอบเฉลี่ยเท่ากัน

หมายเหตุ : คุณยังสามารถเปรียบเทียบค่า F โดยรวมกับค่า F วิกฤต เพื่อพิจารณาว่าคุณควรปฏิเสธสมมติฐานว่างหรือไม่ ในกรณีนี้ เนื่องจากค่าโดยรวมของ F มากกว่าค่าวิกฤตของ F เราจึงปฏิเสธสมมติฐานว่าง โปรดทราบว่าวิธีค่า p และวิธีค่า F วิกฤตจะนำไปสู่ข้อสรุปเดียวกันเสมอ

แหล่งข้อมูลเพิ่มเติม

บทช่วยสอนต่อไปนี้จะอธิบายวิธีดำเนินการ ANOVA ต่างๆ ใน Excel:

วิธีการดำเนินการวิเคราะห์ความแปรปรวนแบบทางเดียวใน Excel
วิธีการดำเนินการวิเคราะห์ความแปรปรวนแบบสองทางใน Excel
วิธีการดำเนินการวัด ANOVA ซ้ำใน Excel
วิธีดำเนินการ ANOVA แบบซ้อนใน Excel