คู่มือฉบับสมบูรณ์: วิธีการตีความผลลัพธ์ anova ใน sas

การวิเคราะห์ความแปรปรวนแบบทางเดียว ใช้เพื่อพิจารณาว่ามีความแตกต่างที่มีนัยสำคัญทางสถิติระหว่างค่าเฉลี่ยของกลุ่มอิสระสามกลุ่มขึ้นไปหรือไม่

ตัวอย่างต่อไปนี้แสดงวิธีตีความผลลัพธ์ของการวิเคราะห์ความแปรปรวนแบบทางเดียวใน SAS

ตัวอย่าง: การตีความผลลัพธ์ ANOVA ใน SAS

สมมติว่านักวิจัยรับสมัครนักศึกษาจำนวน 30 คนเพื่อเข้าร่วมการศึกษาวิจัย นักเรียนจะ ถูกสุ่มให้ ใช้วิธีการศึกษาแบบใดแบบหนึ่งจากสามวิธีเพื่อเตรียมตัวสอบ

ผลการสอบของนักเรียนแต่ละคนแสดงไว้ด้านล่าง:

เราสามารถใช้โค้ดต่อไปนี้เพื่อสร้างชุดข้อมูลนี้ใน SAS:

 /*create dataset*/
data my_data;
    input Method $Score;
    datalines ;
At 78
At 81
At 82
At 82
At 85
At 88
At 88
At 90
B 81
B 83
B 83
B85
B 86
B 88
B90
B91
C 84
C 88
C 88
C 89
C 90
C 93
C 95
C 98
;
run ;

ต่อไป เราจะใช้ proc ANOVA เพื่อทำการวิเคราะห์ความแปรปรวนแบบทางเดียว:

 /*perform one-way ANOVA*/
proc ANOVA data =my_data;
    classMethod ;
    modelScore = Method;
    means Method / tukey cldiff ;
run ;

หมายเหตุ : เราใช้ คำ สั่งหมายถึงพร้อมกับตัวเลือก tukey และ cldiff เพื่อระบุว่าควรทำการทดสอบหลังการทดสอบของ Tukey (ด้วยช่วงความเชื่อมั่น) หากค่า p-value โดยรวมจากการวิเคราะห์ความแปรปรวนแบบทางเดียวมีนัยสำคัญทางสถิติ

ขั้นแรก เราจะดูตาราง ANOVA ในผลลัพธ์:

ต่อไปนี้เป็นวิธีการตีความแต่ละค่าในเอาต์พุต:

โมเดล DF: องศาอิสระสำหรับ วิธีการ แบบแปรผัน ซึ่งคำนวณเป็น #groups -1 ในกรณีนี้ มีวิธีการศึกษาที่แตกต่างกัน 3 วิธี ค่านี้คือ 3-1 = 2

ข้อผิดพลาด DF: องศาอิสระของสิ่งตกค้าง ซึ่งคำนวณเป็น #การสังเกตทั้งหมด – #กลุ่ม ในกรณีนี้ มีการสังเกต 24 รายการและ 3 กลุ่ม ดังนั้นค่านี้จึงเป็น: 24-3 = 21

ผลรวมที่แก้ไขแล้ว : ผลรวมของโมเดล DF และข้อผิดพลาด DF ค่านี้คือ 2 + 21 = 23

โมเดลผลรวมของกำลังสอง: ผลรวมของกำลังสองที่เกี่ยวข้องกับ วิธีการ ของตัวแปร ค่านี้คือ 175.583

ผลรวมของข้อผิดพลาดกำลังสอง: ผลรวมของกำลังสองที่เกี่ยวข้องกับค่าคงเหลือหรือ “ข้อผิดพลาด” ค่านี้คือ 350.25

ผลรวมของ Squares Total ที่แก้ไขแล้ว : ผลรวมของโมเดล SS และข้อผิดพลาด SS ค่านี้คือ 525.833

แบบจำลองกำลังสองเฉลี่ย: ผลรวมเฉลี่ยของกำลังสองที่เกี่ยวข้องกับ วิธีการ ซึ่งคำนวณเป็นรุ่น SS / รุ่น DF หรือ 175.583 / 2 = 87.79

ค่าคลาดเคลื่อนกำลังสองเฉลี่ย: ผลรวมเฉลี่ยของกำลังสองที่เกี่ยวข้องกับค่าคงเหลือ ซึ่งคำนวณเป็นข้อผิดพลาด SS / ข้อผิดพลาด DF ซึ่งก็คือ 350.25 / 21 = 16.68

ค่า F: สถิติ F โดยรวมของแบบจำลอง ANOVA ซึ่งคำนวณเป็นโมเดลค่าเฉลี่ยกำลังสอง/ค่าคลาดเคลื่อนกำลังสองเฉลี่ย หรือ 87.79/16.68 = 5.26

Pr >F: ค่า p ที่เกี่ยวข้องกับสถิติ F โดยมีตัวเศษ df = 2 และตัวส่วน df = 21 ในกรณีนี้ ค่า p จะเป็น 0.0140

ค่าที่สำคัญที่สุดในชุดผลลัพธ์คือค่า p เนื่องจากจะบอกเราว่าค่าเฉลี่ยของทั้งสามกลุ่มมีความแตกต่างอย่างมีนัยสำคัญหรือไม่

โปรดจำไว้ว่าการวิเคราะห์ความแปรปรวนทางเดียวใช้สมมติฐานว่างและทางเลือกต่อไปนี้:

• H ₀ (สมมติฐานว่าง): ค่าเฉลี่ยกลุ่มทั้งหมดเท่ากัน
• H _A (สมมติฐานทางเลือก): ค่าเฉลี่ยกลุ่มอย่างน้อยหนึ่งกลุ่มแตกต่างจากค่าเฉลี่ยอื่นๆ

เนื่องจากค่า p ในตาราง ANOVA ของเรา (0.0140) น้อยกว่า 0.05 เราจึงปฏิเสธสมมติฐานว่าง

ซึ่งหมายความว่าเรามีหลักฐานเพียงพอที่จะบอกว่าคะแนนสอบเฉลี่ยของวิธีการศึกษาทั้ง 3 วิธีไม่เท่ากัน

เพื่อพิจารณาว่าค่าเฉลี่ยของกลุ่มใดที่แตกต่างกัน เราต้องอ้างอิงตารางผลลัพธ์สุดท้ายซึ่งแสดงผลการทดสอบหลังการทดสอบของ Tukey:

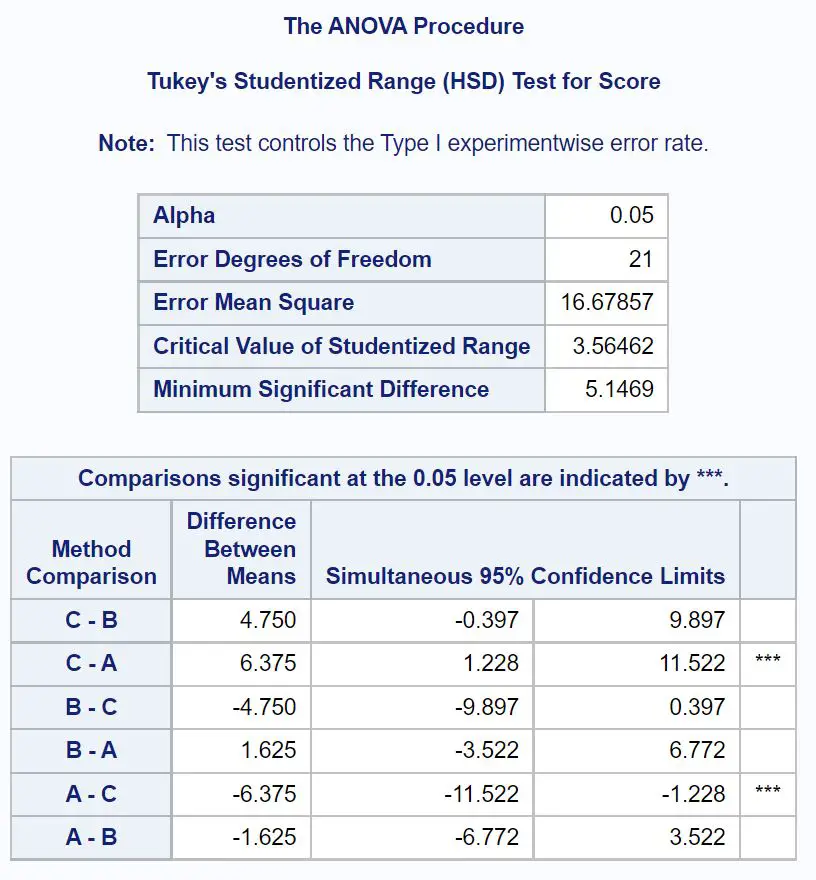
หากต้องการทราบว่าค่าเฉลี่ยของกลุ่มใดแตกต่างกัน เราต้องดูว่าการเปรียบเทียบแบบคู่ใดมีดาว ( *** ) อยู่ข้างๆ

ตารางแสดงให้เห็นว่าคะแนนสอบเฉลี่ยระหว่างกลุ่ม A และกลุ่ม C มีความแตกต่างอย่างมีนัยสำคัญทางสถิติ

โดยเฉพาะความแตกต่างโดยเฉลี่ยของคะแนนสอบระหว่างกลุ่ม C และกลุ่ม A คือ 6.375

ช่วงความเชื่อมั่น 95% สำหรับผลต่างเฉลี่ยคือ [1.228, 11.522]

ไม่มีความแตกต่างที่มีนัยสำคัญทางสถิติระหว่างค่าเฉลี่ยของกลุ่มอื่นๆ

แหล่งข้อมูลเพิ่มเติม

บทช่วยสอนต่อไปนี้ให้ข้อมูลเพิ่มเติมเกี่ยวกับแบบจำลอง ANOVA:

คู่มือการใช้การทดสอบหลังการทดลองด้วย ANOVA
วิธีดำเนินการวิเคราะห์ความแปรปรวนแบบทางเดียวใน SAS
วิธีดำเนินการ ANOVA แบบสองทางใน SAS