ความรู้เบื้องต้นเกี่ยวกับการจำแนกประเภทและการถดถอยต้นไม้

เมื่อความสัมพันธ์ระหว่างชุดของตัวแปรทำนายและ ตัวแปรตอบสนอง เป็นแบบเส้นตรง วิธีการต่างๆ เช่น การถดถอยเชิงเส้นหลายตัว จะสามารถสร้างแบบจำลองการทำนายที่แม่นยำได้

อย่างไรก็ตาม เมื่อความสัมพันธ์ระหว่างชุดตัวทำนายและการตอบสนองมีความไม่เชิงเส้นและซับซ้อนอย่างมาก วิธีการไม่เชิงเส้นอาจทำงานได้ดีกว่า

ตัวอย่างของวิธีการแบบไม่เชิงเส้นคือ แผนผังการจำแนกประเภทและการถดถอย ซึ่งมักใช้อักษรย่อว่า CART

ตามชื่อที่แนะนำ โมเดล CART ใช้ชุดของตัวแปรทำนายเพื่อสร้าง แผนผังการตัดสินใจ ที่ทำนายค่าของตัวแปรตอบสนอง

ตัวอย่างเช่น สมมติว่าเรามีชุดข้อมูลที่มีตัวแปรทำนายจำนวน ปีที่เล่น และ โฮมรันเฉลี่ย และตัวแปรการตอบสนอง เงินเดือนประจำปี สำหรับนักเบสบอลมืออาชีพหลายร้อยคน

แผนผังการถดถอยอาจมีลักษณะดังนี้สำหรับชุดข้อมูลนี้:

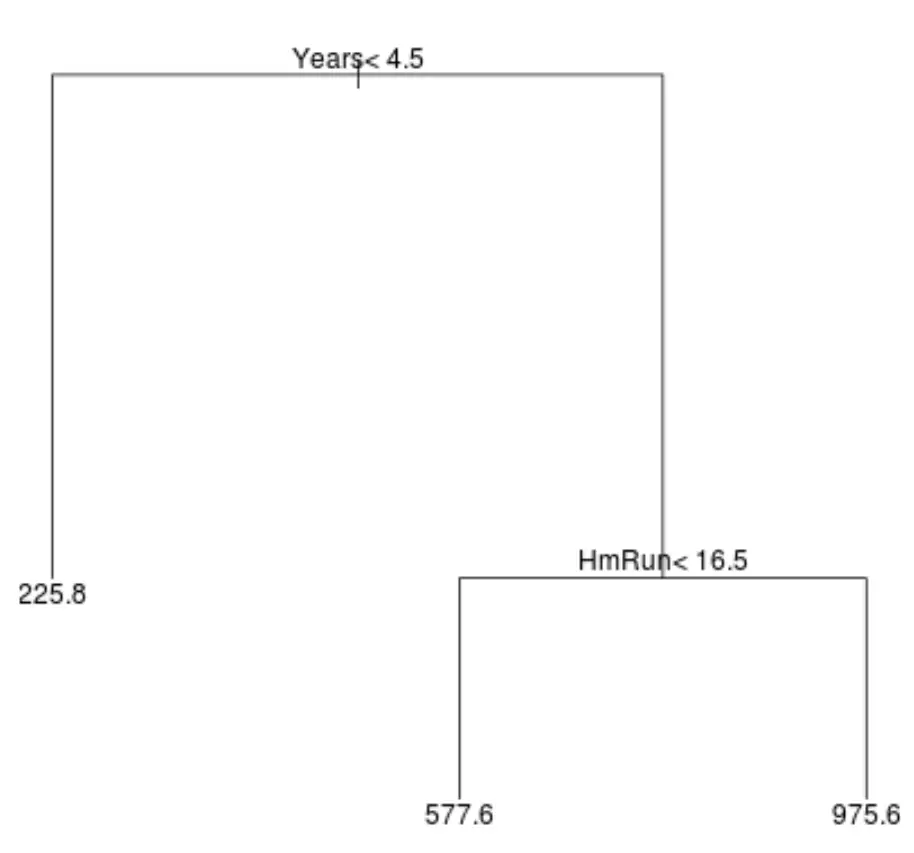
วิธีการตีความต้นไม้มีดังนี้:

• ผู้เล่นที่เล่นน้อยกว่า 4.5 ปีจะมีเงินเดือนที่คาดการณ์ไว้ที่ 225.8k
• ผู้เล่นที่เล่นมากกว่า 4.5 ปีหรือมากกว่าและน้อยกว่า 16.5 โฮมรันโดยเฉลี่ยจะมีเงินเดือนที่คาดการณ์ไว้ที่ 577.6K
• ผู้เล่นที่มีประสบการณ์การเล่น 4.5 ปีขึ้นไป และโฮมรันเฉลี่ย 16.5 ครั้งขึ้นไป มีเงินเดือนที่คาดหวังอยู่ที่ 975.6K ดอลลาร์

ผลลัพธ์ของแบบจำลองนี้น่าจะสมเหตุสมผล โดยสังหรณ์ใจ ผู้เล่นที่มีประสบการณ์มากกว่าและโฮมรันโดยเฉลี่ยมากกว่ามักจะได้รับเงินเดือนสูงกว่า

จากนั้นเราก็สามารถใช้โมเดลนี้ทำนายเงินเดือนของผู้เล่นใหม่ได้

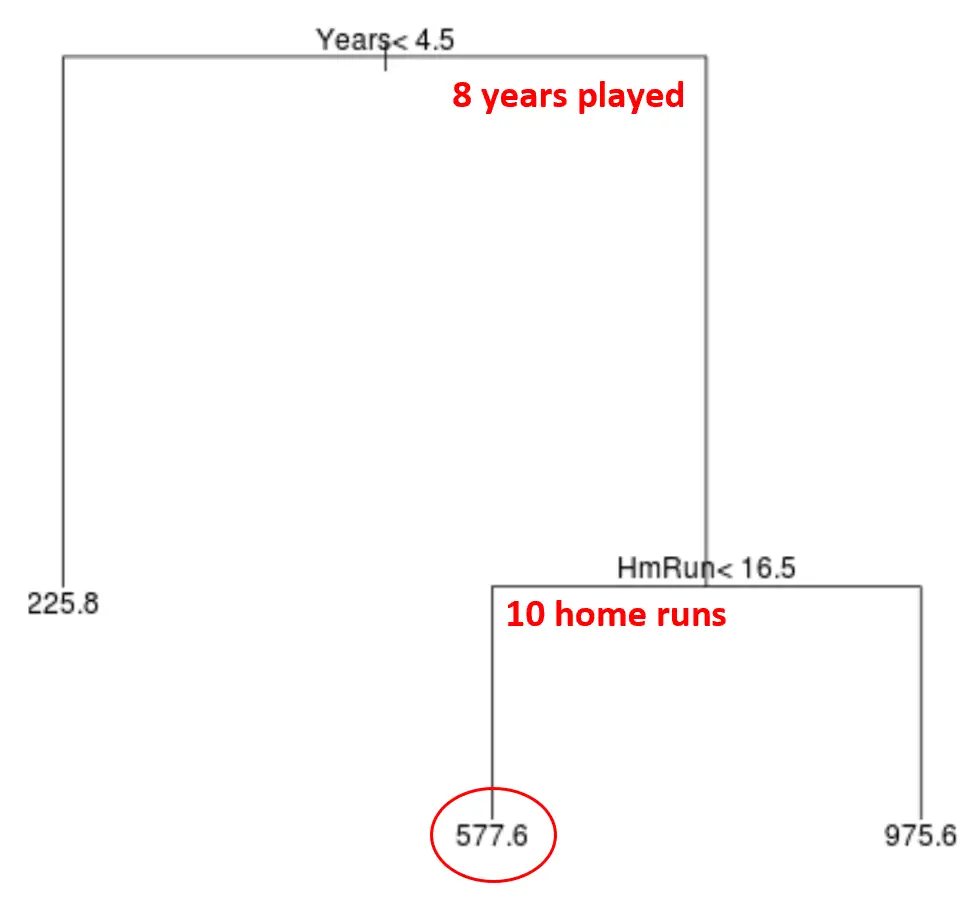
ตัวอย่างเช่น สมมติว่าผู้เล่นคนใดคนหนึ่งเล่นมา 8 ปีและโฮมรันเฉลี่ย 10 ครั้งต่อปี ตามแบบจำลองของเรา เราจะคาดการณ์ว่าผู้เล่นรายนี้จะมีเงินเดือนประจำปีอยู่ที่ 577.6,000 ดอลลาร์

ข้อสังเกตบางประการเกี่ยวกับต้นไม้:

• ตัวแปรทำนายตัวแรกที่อยู่ด้านบนสุดของแผนผังคือตัวแปรที่สำคัญที่สุด กล่าวคือตัวแปรที่มีอิทธิพลมากที่สุดต่อการทำนายค่าของตัวแปรตอบสนอง ในกรณีนี้ ปีที่เล่น จะทำนายเงินเดือนได้ดีกว่า ค่าเฉลี่ยของวงจร
• บริเวณด้านล่างของต้นไม้เรียกว่า โหนดใบ ต้นไม้ต้นนี้มีโหนดเทอร์มินัลสามโหนด

ขั้นตอนการสร้างโมเดล CART

เราสามารถใช้ขั้นตอนต่อไปนี้เพื่อสร้างแบบจำลอง CART สำหรับชุดข้อมูลที่กำหนด:

ขั้นตอนที่ 1: ใช้การแยกไบนารีแบบเรียกซ้ำเพื่อขยายต้นไม้ขนาดใหญ่ในข้อมูลการฝึก

ขั้นแรก เราใช้อัลกอริธึม โลภ ที่เรียกว่าการแยกไบนารีแบบเรียกซ้ำเพื่อสร้างแผนภูมิการถดถอยโดยใช้วิธีการต่อไปนี้:

• พิจารณาตัวแปรทำนายทั้งหมด X _{1 ,} X ₂ , … , ความคลาดเคลื่อนมาตรฐานตกค้าง) ต่ำสุด .
  • สำหรับแผนผังการจำแนกประเภท เราเลือกตัวทำนายและจุดตัดเพื่อให้แผนภูมิผลลัพธ์มีอัตราข้อผิดพลาดในการจำแนกประเภทต่ำที่สุด
• ทำซ้ำขั้นตอนนี้ โดยหยุดเฉพาะเมื่อโหนดเทอร์มินัลแต่ละโหนดมีจำนวนการสังเกตน้อยกว่าจำนวนขั้นต่ำที่กำหนดเท่านั้น

อัลกอริธึมนี้เป็นอะไร ที่โลภมาก เพราะในแต่ละขั้นตอนของกระบวนการสร้างแผนผังจะเป็นตัวกำหนดการแยกที่ดีที่สุดตามขั้นตอนนั้นเท่านั้น แทนที่จะมองไปในอนาคตและเลือกการแยกที่จะนำไปสู่แผนผังทั่วโลกที่ดีขึ้นในระยะอนาคต

ขั้นตอนที่ 2: ใช้การตัดแต่งกิ่งที่ซับซ้อนด้านต้นทุนกับต้นไม้ใหญ่เพื่อให้ได้ลำดับต้นไม้ที่ดีที่สุด โดยยึดตาม α

เมื่อเราปลูกต้นไม้ใหญ่ได้แล้ว เราก็ต้อง ตัดแต่ง กิ่งโดยใช้วิธีการที่เรียกว่าการตัดแต่งกิ่งแบบซับซ้อน ซึ่งมีการทำงานดังนี้

• สำหรับแต่ละแผนผังที่เป็นไปได้ที่มีโหนดเทอร์มินัล T ให้ค้นหาแผนผังที่ย่อ RSS + α|T| ให้เหลือน้อยที่สุด
• โปรดทราบว่าเมื่อเราเพิ่มค่าของ α ต้นไม้ที่มีโหนดเทอร์มินัลมากกว่าจะถูกลงโทษ เพื่อให้แน่ใจว่าต้นไม้จะไม่ซับซ้อนเกินไป

กระบวนการนี้ส่งผลให้เกิดลำดับแผนผังที่ดีที่สุดสำหรับแต่ละค่าของ α

ขั้นตอนที่ 3: ใช้การตรวจสอบข้าม k-fold เพื่อเลือก α

เมื่อเราพบแผนผังที่ดีที่สุดสำหรับแต่ละค่าของ α แล้ว เราสามารถใช้ การตรวจสอบความถูกต้องข้ามแบบ k-fold เพื่อเลือกค่าของ α ที่จะช่วยลดข้อผิดพลาดในการทดสอบให้เหลือน้อยที่สุด

ขั้นตอนที่ 4: เลือกเทมเพลตสุดท้าย

สุดท้าย เราเลือกโมเดลสุดท้ายเป็นโมเดลที่สอดคล้องกับค่าที่เลือกของ α

ข้อดีและข้อเสียของรุ่น CART

รุ่น CART มี ข้อดี ดังต่อไปนี้:

• ง่ายต่อการตีความ
• อธิบายได้ง่าย
• ง่ายต่อการมองเห็น
• สามารถนำไปใช้กับทั้งปัญหา การถดถอยและการจัดหมวดหมู่

อย่างไรก็ตาม โมเดล CART มี ข้อเสียดังต่อไปนี้:

• พวกเขามีแนวโน้มที่จะไม่มีความแม่นยำในการคาดการณ์มากเท่ากับอัลกอริธึมการเรียนรู้ของเครื่องที่ไม่ใช่เชิงเส้นอื่นๆ อย่างไรก็ตาม การจัดกลุ่มแผนผังการตัดสินใจหลายๆ แบบด้วยวิธีต่างๆ เช่น การบรรจุถุง การเพิ่มระดับ และการสุ่มป่า จะทำให้ความแม่นยำในการทำนายของต้นไม้เหล่านี้ได้รับการปรับปรุงให้ดีขึ้น

ที่เกี่ยวข้อง: วิธีการจัดหมวดหมู่และการถดถอยต้นไม้ใน R