วิธีการใช้ทฤษฎีบทขีด จำกัด กลางใน excel

ทฤษฎีบทขีดจำกัดกลาง ระบุว่าการกระจายตัวตัวอย่างของค่าเฉลี่ยตัวอย่างจะอยู่ที่ประมาณปกติ หากขนาดตัวอย่างมีขนาดใหญ่เพียงพอ แม้ว่าการกระจายตัวของประชากรจะไม่ปกติก็ตาม

ทฤษฎีบทขีดจำกัดกลางยังระบุด้วยว่าการกระจายตัวอย่างจะมีคุณสมบัติดังต่อไปนี้:

1. ค่าเฉลี่ยของการกระจายตัวอย่างจะเท่ากับค่าเฉลี่ยของการกระจายตัวของประชากร:

x = ไมโคร

2. ค่าเบี่ยงเบนมาตรฐานของการกระจายตัวอย่างจะเท่ากับค่าเบี่ยงเบนมาตรฐานของประชากรหารด้วยขนาดตัวอย่าง:

s = σ / √n

ในบทช่วยสอนนี้ เราจะอธิบายวิธีใช้ทฤษฎีบทขีดจำกัดกลางใน Excel กับการแจกแจงที่กำหนด

การใช้ทฤษฎีบทขีด จำกัด กลางใน Excel

สมมติว่าเรามีการแจกแจงที่มีค่าเฉลี่ย 8 และค่าเบี่ยงเบนมาตรฐาน 4 เราสามารถใช้สูตรต่อไปนี้ใน Excel เพื่อค้นหาทั้งค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐานของการกระจายตัวอย่างด้วยขนาดตัวอย่าง 15 :

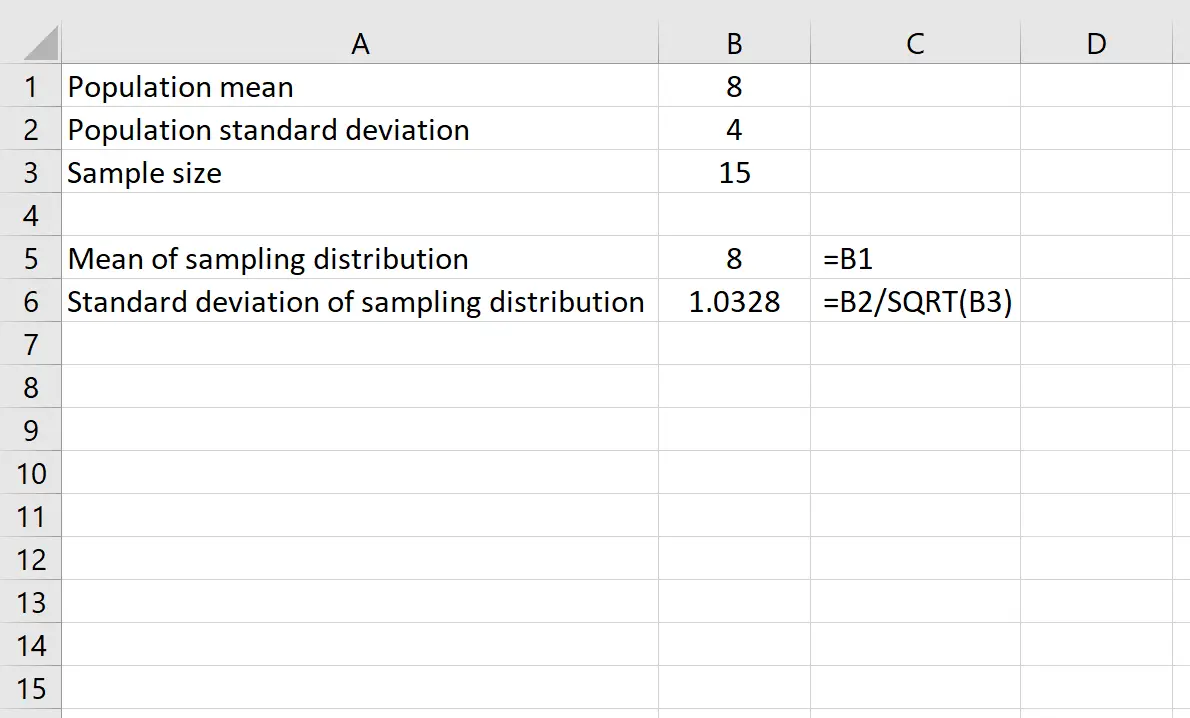
ค่าเฉลี่ยของการกระจายตัวอย่างเท่ากับค่าเฉลี่ยของการกระจายตัวของประชากร ซึ่งก็คือ 8

ค่าเบี่ยงเบนมาตรฐานของการกระจายตัวอย่างเท่ากับค่าเบี่ยงเบนมาตรฐานของประชากรหารด้วยขนาดตัวอย่าง หรือ: 4 /√15 = 1.0328

นอกจากนี้เรายังสามารถใช้ทฤษฎีบทขีดจำกัดกลางเพื่อตอบคำถามเกี่ยวกับความน่าจะเป็นได้ ตัวอย่างเช่น หากประชากรที่กำหนดมีค่าเฉลี่ย 8 และส่วนเบี่ยงเบนมาตรฐานเป็น 4 ความน่าจะเป็นที่กลุ่มตัวอย่างที่กำหนดขนาด 15 เป็นเท่าใด   มีค่าเฉลี่ยน้อยกว่าหรือเท่ากับ 7 ?

เพื่อตอบคำถามนี้ เราสามารถใช้ฟังก์ชัน NORM.DIST() ใน Excel ซึ่งใช้ไวยากรณ์ต่อไปนี้:

NORM.DIST(x, เฉลี่ย, standard_dev, สะสม)

ทอง:

• x: ตัวอย่างหมายความว่าคุณต้องการทดสอบ
• ค่าเฉลี่ย: ค่าเฉลี่ยที่คาดหวังของการกระจายตัวอย่าง
• standard_dev: ค่าเบี่ยงเบนมาตรฐานที่คาดหวังของการกระจายตัวอย่าง
• สะสม: TRUE ส่งคืนค่า CDF ปกติ FALSE ส่งกลับค่าของ PDF ปกติ ในกรณีของเรา เราจะใช้ TRUE เสมอ

ฟังก์ชันนี้จะคืนค่าความน่าจะเป็นที่ค่าเฉลี่ยตัวอย่างน้อยกว่าหรือเท่ากับค่าที่กำหนด

นี่คือสูตรที่เราจะใช้ในตัวอย่างนี้:

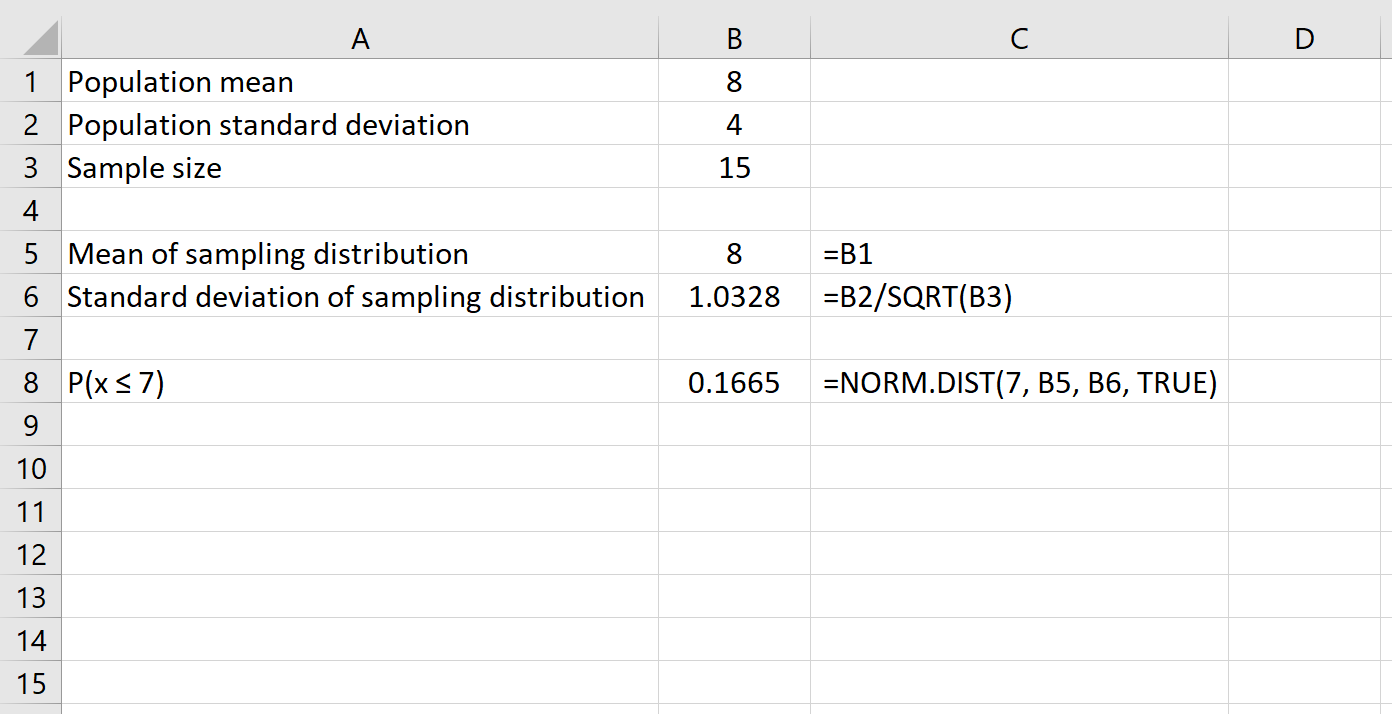
นี่บอกเราว่าสำหรับประชากรที่มีค่าเฉลี่ย 8 และค่าเบี่ยงเบนมาตรฐาน 4 ความน่าจะเป็นที่กลุ่มตัวอย่างที่กำหนดขนาด 15   มีค่าเฉลี่ยน้อยกว่าหรือเท่ากับ 7 หรือ 0.1665

นอกจากนี้เรายังสามารถค้นหาความน่าจะเป็นที่ขนาดตัวอย่างที่กำหนดจะมีค่าเฉลี่ย มากกว่า จำนวนที่กำหนดได้โดยใช้สูตร 1 – NORM.DIST()

ตัวอย่างเช่น สูตรต่อไปนี้แสดงวิธีหาความน่าจะเป็นที่ขนาดตัวอย่างที่กำหนดเป็น 15 จะมีค่าเฉลี่ย มากกว่า 7:

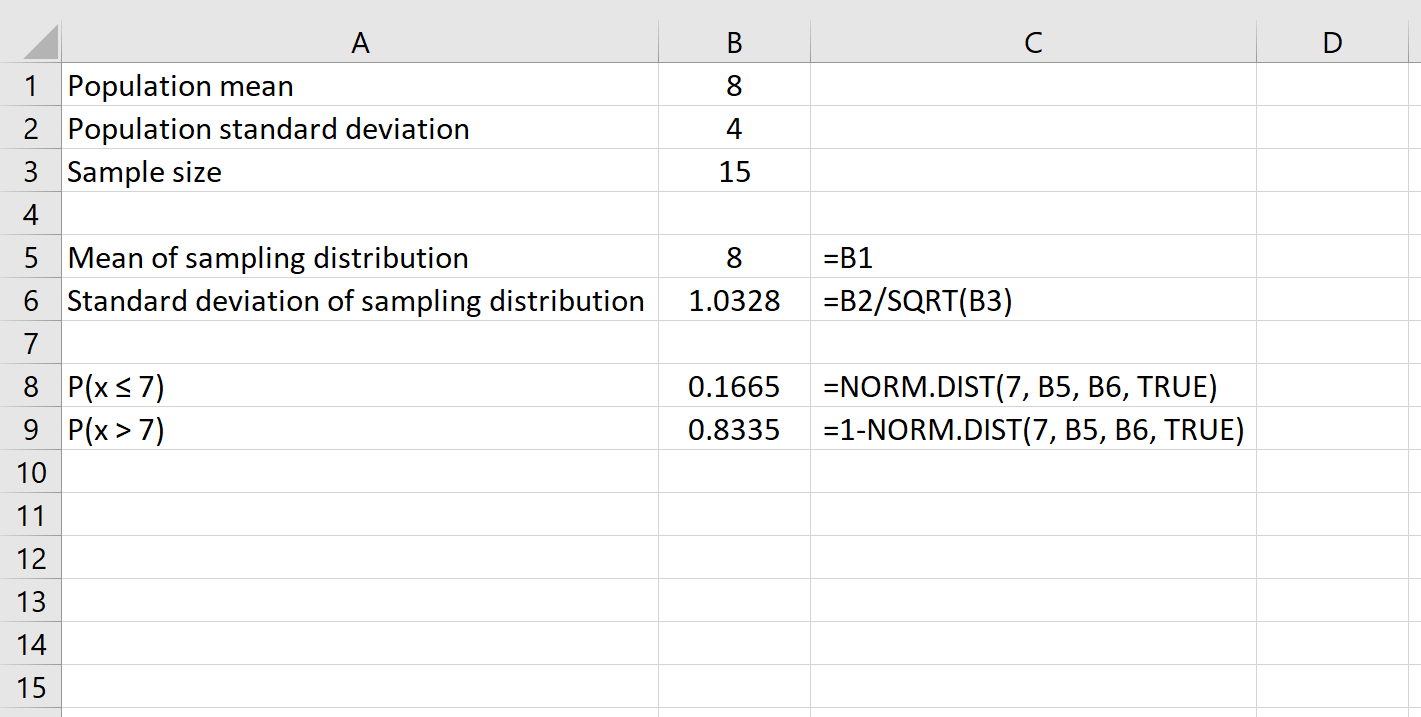
สุดท้ายนี้ เราสามารถค้นหาความน่าจะเป็นที่ขนาดตัวอย่างที่กำหนดจะมีค่าเฉลี่ย ระหว่าง ตัวเลขสองตัวได้ โดยใช้สูตร NORM.DIST(ตัวเลขที่ใหญ่กว่า) – NORM.DIST(ตัวเลขที่น้อยกว่า)

ตัวอย่างเช่น สูตรต่อไปนี้แสดงวิธีค้นหาความน่าจะเป็นที่ขนาดตัวอย่างที่กำหนดเป็น 15 มีค่าเฉลี่ยระหว่าง 7 ถึง 9:

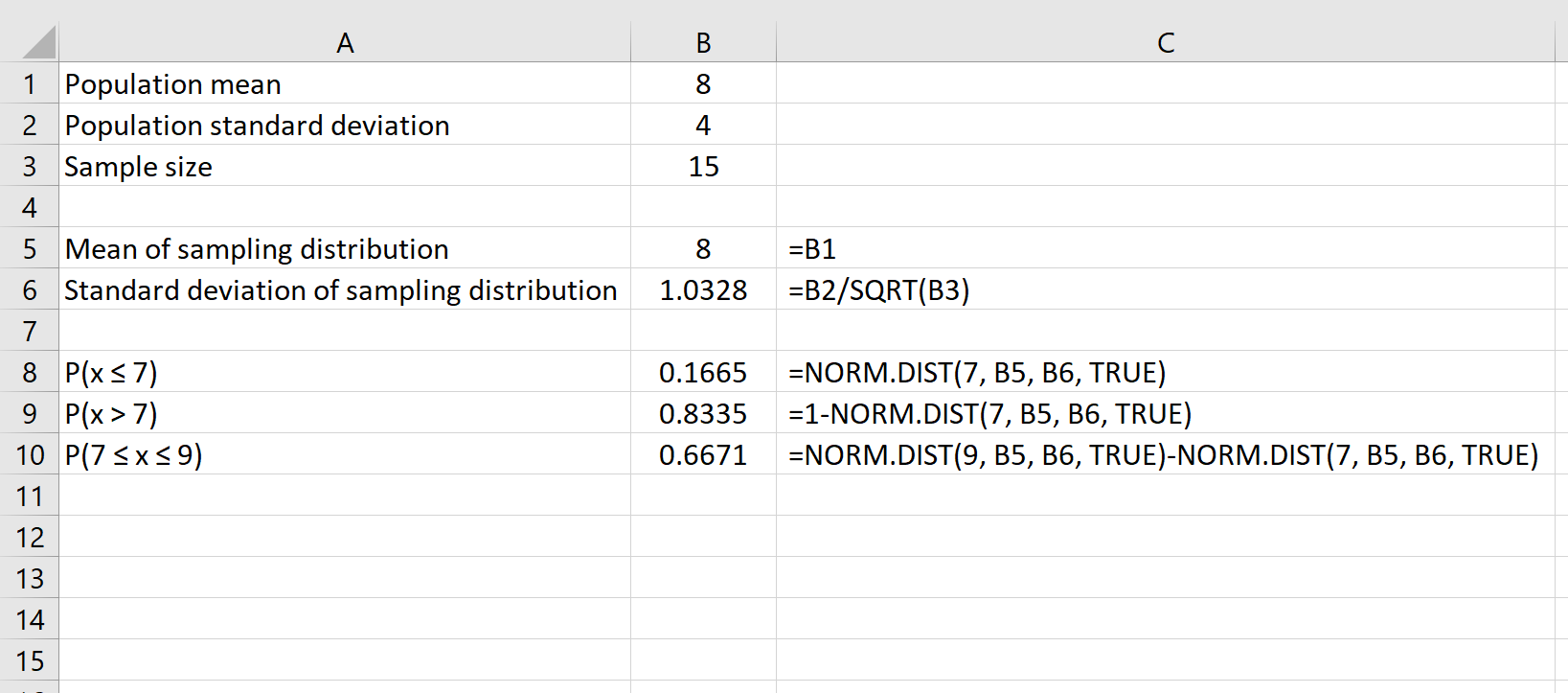
แหล่งข้อมูลเพิ่มเติม

เครื่องคำนวณทฤษฎีบทขีดจำกัดกลาง
วิธีการใช้กฎทั่วไปใน Excel
วิธีการสร้างเส้นโค้งระฆังใน Excel