วิธีใช้ทฤษฎีบทขีดจำกัดกลางกับเครื่องคิดเลข ti-84

ทฤษฎีบทขีดจำกัดกลาง ระบุว่าการกระจายตัวตัวอย่างของค่าเฉลี่ยตัวอย่างจะอยู่ที่ประมาณปกติ หากขนาดตัวอย่างมีขนาดใหญ่เพียงพอ แม้ว่าการกระจายตัวของประชากรจะไม่ปกติก็ตาม

ทฤษฎีบทขีดจำกัดกลางยังระบุด้วยว่าการกระจายตัวอย่างจะมีคุณสมบัติดังต่อไปนี้:

1. ค่าเฉลี่ยของการกระจายตัวอย่างจะเท่ากับค่าเฉลี่ยของการกระจายตัวของประชากร:

x = ไมโคร

2. ค่าเบี่ยงเบนมาตรฐานของการกระจายตัวอย่างจะเท่ากับค่าเบี่ยงเบนมาตรฐานของประชากรหารด้วยขนาดตัวอย่าง:

s = σ / √n

ในการค้นหาความน่าจะเป็นที่เกี่ยวข้องกับค่าเฉลี่ยตัวอย่างบนเครื่องคิดเลข TI-84 เราสามารถใช้ฟังก์ชัน Normalcdf() โดยมีไวยากรณ์ต่อไปนี้:

 normalcdf (lower value, upper value, x , s/√ n )

ทอง:

• x : ค่าเฉลี่ยตัวอย่าง
• s : ค่าเบี่ยงเบนมาตรฐานตัวอย่าง
• n : ขนาดตัวอย่าง

หากต้องการเข้าถึงฟังก์ชันนี้บนเครื่องคิดเลข TI-84 เพียงกด 2 จากนั้น กด VARS จากนั้นเลื่อนไปที่ Normalcdf ( และกด ENTER

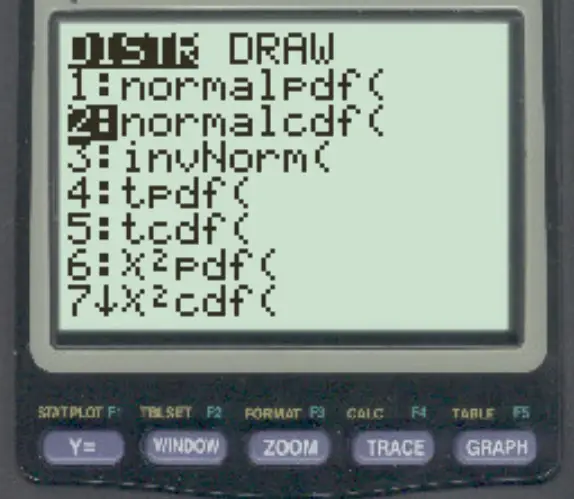
ตัวอย่างต่อไปนี้แสดงวิธีใช้ฟังก์ชันนี้ในทางปฏิบัติ

ตัวอย่างที่ 1: ค้นหาความน่าจะเป็นระหว่างสองค่า

การแจกแจงมีค่าเฉลี่ย 70 และค่าเบี่ยงเบนมาตรฐาน 7 หากเราเลือกตัวอย่างสุ่มที่มีขนาด n = 35 ให้ค้นหาความน่าจะเป็นที่ค่าเฉลี่ยตัวอย่างอยู่ระหว่าง 68 ถึง 72

เราสามารถใช้ไวยากรณ์ต่อไปนี้บน TI-84:

 normalcdf (68, 72, 70, 7/√ 35 ) 

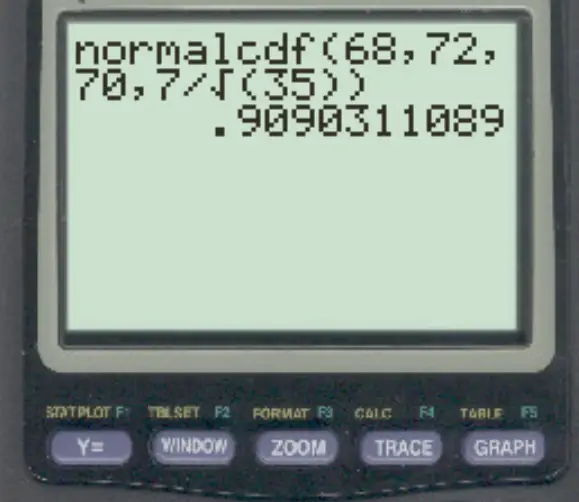
ความน่าจะเป็นที่ค่าเฉลี่ยตัวอย่างอยู่ระหว่าง 68 ถึง 72 คือ 0.909

ตัวอย่างที่ 2: การค้นหาความน่าจะเป็นที่มากกว่าค่า

การแจกแจงมีค่าเฉลี่ย 50 และค่าเบี่ยงเบนมาตรฐาน 4 หากเราเลือกตัวอย่างสุ่มที่มีขนาด n = 30 ให้ค้นหาความน่าจะเป็นที่ค่าเฉลี่ยตัวอย่างมากกว่า 48

เราสามารถใช้ไวยากรณ์ต่อไปนี้บน TI-84:

 normalcdf (48, E99, 50, 4/√ 30 )

หมายเหตุ: คุณสามารถเข้าถึงสัญลักษณ์ “E” ได้โดยกด 2 จากนั้นกดปุ่ม ,

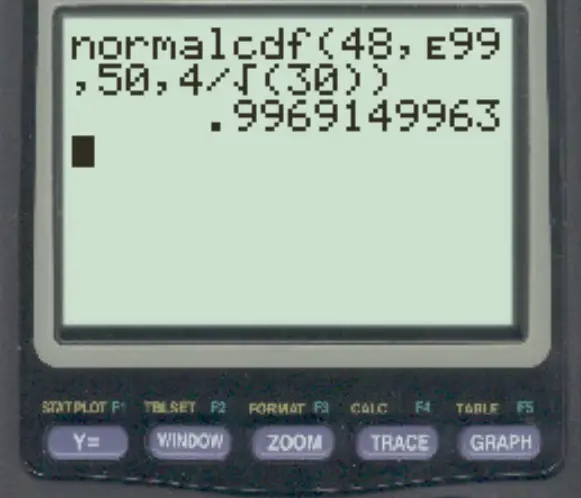
ความน่าจะเป็นที่ค่าเฉลี่ยตัวอย่างมากกว่า 48 คือ 0.9969

ตัวอย่างที่ 3: การค้นหาความน่าจะเป็นที่น้อยกว่าค่า

การแจกแจงมีค่าเฉลี่ย 20 และค่าเบี่ยงเบนมาตรฐาน 3 หากเราเลือกตัวอย่างสุ่มที่มีขนาด n = 40 ให้ค้นหาความน่าจะเป็นที่ค่าเฉลี่ยตัวอย่างน้อยกว่า 19

เราสามารถใช้ไวยากรณ์ต่อไปนี้บน TI-84:

 normalcdf (-E99, 19, 20, 3/√ 40 ) 

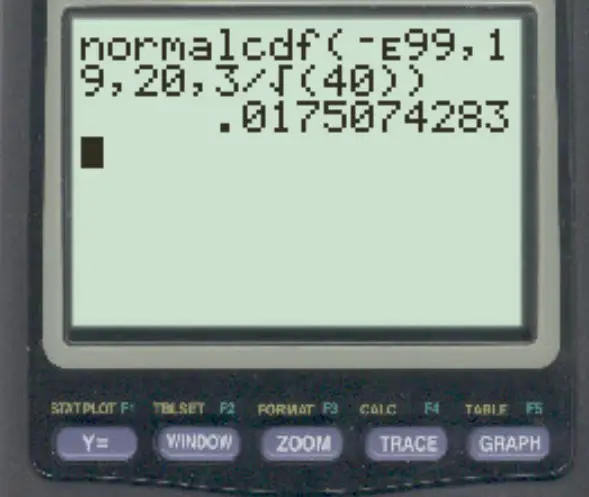
ความน่าจะเป็นที่ค่าเฉลี่ยตัวอย่างน้อยกว่า 19 คือ 0.0175

แหล่งข้อมูลเพิ่มเติม

ความรู้เบื้องต้นเกี่ยวกับทฤษฎีบทขีดจำกัดศูนย์กลาง
เครื่องคำนวณทฤษฎีบทขีดจำกัดกลาง
วิธีการใช้ทฤษฎีบทขีด จำกัด กลางใน Excel
ทฤษฎีบทขีดจำกัดศูนย์กลาง: เงื่อนไขสี่ประการที่ต้องปฏิบัติตาม