ทฤษฎีบทของเบย์

โดย ดร.เบนจามิน แอนเดอร์สัน สิงหาคม 1, 2023 ความน่าจะเป็น 0 ความคิดเห็น

บทความนี้จะอธิบายว่าทฤษฎีบทของเบย์คืออะไร และใช้เพื่ออะไรในด้านความน่าจะเป็นและสถิติ ดังนั้น คุณจะค้นพบว่าสูตรของทฤษฎีบทของเบย์คืออะไร ตัวอย่างที่ได้รับการแก้ไขของทฤษฎีบทของเบย์ และการประยุกต์ของทฤษฎีบทนี้คืออะไร

ทฤษฎีบทของเบย์สคืออะไร?

ในทฤษฎีความน่าจะ เป็น ทฤษฎีบทของเบย์ เป็นกฎที่ใช้ในการคำนวณความน่าจะเป็นของเหตุการณ์เมื่อทราบข้อมูลเชิงนิรนัยเกี่ยวกับเหตุการณ์นั้น

โดยเฉพาะอย่างยิ่ง ทฤษฎีบทของเบย์เชื่อมโยงความน่าจะเป็นของเหตุการณ์ A ที่กำหนดเหตุการณ์ B กับความน่าจะเป็นของ B ที่กำหนด A ในทางคณิตศาสตร์

ตัวอย่างเช่น หากคุณทราบล่วงหน้าถึงความน่าจะเป็นที่บุคคลนั้นจะปวดหัวเมื่อเป็นไข้หวัดใหญ่ คุณสามารถใช้ทฤษฎีบทของเบย์เพื่อกำหนดความน่าจะเป็นที่บุคคลนั้นจะป่วยเป็นไข้หวัดใหญ่เมื่อพวกเขาปวดหัว

ทฤษฎีบทของเบย์มีการนำไปประยุกต์ใช้มากมาย เช่น ใช้ในทางการแพทย์ เศรษฐศาสตร์ หรือเทคโนโลยีเพื่อคำนวณความน่าจะเป็นของเหตุการณ์บางอย่างที่กำหนดโดยเหตุการณ์อื่น ด้านล่างนี้ เราจะลงรายละเอียดเกี่ยวกับการประยุกต์ต่างๆ ของทฤษฎีบทของเบย์

ทฤษฎีบทของเบย์สถูกคิดค้นโดยนักคณิตศาสตร์ชาวอังกฤษ โธมัส เบย์ส (ค.ศ. 1702-1761) แม้ว่าจะได้รับการตีพิมพ์หลังมรณกรรมในปี ค.ศ. 1763 ก็ตาม

➤ ดู: ความน่าจะเป็นแบบมีเงื่อนไข

สูตรทฤษฎีบทของเบย์

ทฤษฎีบทของเบย์กล่าวว่า เมื่อพิจารณาจากสเปซตัวอย่างที่ประกอบด้วยชุดของ เหตุการณ์ที่ไม่เกิดร่วมกัน {A ₁ , A ₂ ,…, A _i ,…, A _n } ซึ่งความน่าจะเป็นไม่เป็นศูนย์และอีกเหตุการณ์หนึ่ง B เราสามารถเชื่อมโยงเงื่อนไขทางคณิตศาสตร์ได้ ความน่าจะเป็นของ A _i เมื่อได้รับเหตุการณ์ B ด้วยความน่าจะเป็นแบบมีเงื่อนไขของ B เมื่อให้ A _i

ดังนั้น สูตรสำหรับทฤษฎีบทของเบย์ หรือที่เรียกว่า กฎของเบย์ คือ:

ทอง:

$P(A_i|B)$

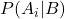
คือความน่าจะเป็นแบบมีเงื่อนไขของเหตุการณ์ A _{เมื่อ} ให้เหตุการณ์ B เรียกว่าความน่าจะเป็นภายหลัง
$P(B|A_i)$

คือความน่าจะเป็นแบบมีเงื่อนไขของเหตุการณ์ B เมื่อพิจารณาจากเหตุการณ์ A _i
$P(A_i)$

คือความน่าจะเป็นที่เหตุการณ์ A _i จะเกิดขึ้น เรียกว่าความน่าจะเป็นแบบนิรนัย

โปรดทราบว่าตัวส่วนของสูตรทฤษฎีบทของเบย์คือ ความน่าจะเป็นรวม ของเหตุการณ์ B

ตัวอย่างทฤษฎีบทของเบย์

เมื่อเราเห็นคำจำกัดความของทฤษฎีบทเบย์และสูตรของมัน เราจะเห็นตัวอย่างที่ได้รับการแก้ไขแล้วของวิธีการคำนวณความน่าจะเป็นด้วยทฤษฎีบทเบย์เพื่อให้เข้าใจแนวคิดได้ดีขึ้น

ร้านขายเครื่องใช้ไฟฟ้าขายโทรทัศน์สามยี่ห้อ: X, Y, Z ประมาณว่า 20% ของยอดขายเป็นโทรทัศน์ของแบรนด์มีข้อบกพร่อง โทรทัศน์แบรนด์ Y 3% มีข้อบกพร่อง และโทรทัศน์แบรนด์ Z 4% มีข้อบกพร่อง เมื่อพิจารณาว่าทีวีมีข้อบกพร่อง ความน่าจะเป็นที่จะเป็น Brand Z TV เป็นเท่าใด

แบบฝึกหัดนี้ทำให้เรามีความน่าจะเป็นที่ลูกค้าจะซื้อโทรทัศน์แต่ละยี่ห้อ:

เหตุการณ์ A ₁ : ลูกค้าซื้อโทรทัศน์ยี่ห้อ X → P(A ₁ )=0.20
เหตุการณ์ A ₂ : ลูกค้าซื้อโทรทัศน์ยี่ห้อ Y → P(A ₂ )=0.50
เหตุการณ์ A ₃ : ลูกค้าซื้อโทรทัศน์ยี่ห้อ Z → P(A ₃ )=0.30

นอกจากนี้ การอ่านยังช่วยให้เรามีความน่าจะเป็นที่โทรทัศน์แต่ละยี่ห้อจะเสีย:

เหตุการณ์ B: ทีวีมีข้อบกพร่อง

B|A ₁ : เมื่อพิจารณาจากโทรทัศน์ยี่ห้อ X โทรทัศน์มีข้อบกพร่อง → P(B|A ₁ )=0.05
B|A ₂ : เมื่อพิจารณาจากโทรทัศน์ยี่ห้อ Y โทรทัศน์มีข้อบกพร่อง → P(B|A ₂ )=0.03
B|A ₃ : เมื่อพิจารณาจากโทรทัศน์ยี่ห้อ Z โทรทัศน์มีข้อบกพร่อง → P(B|A ₃ )=0.04

ดังนั้น แผนผังความน่าจะ เป็นของเหตุการณ์ทั้งหมดที่เราสนใจจึงเป็นดังนี้:

ดังนั้น ในการคำนวณความน่าจะเป็นที่โทรทัศน์ที่มีข้อบกพร่องคือแบรนด์ Z เราต้องใช้สูตรจากทฤษฎีบทของเบย์:

$P(A_i|B)=\cfrac{P(B|A_i)\cdot P(A_i)}{\displaystyle \sum_{k=1}^n P(B|A_k)\cdot P(A_k)}$

เมื่อใช้คำศัพท์ที่ใช้ในตัวอย่างนี้ สูตรของ Bayes จะมีลักษณะดังนี้:

$P(A_3|B)=\cfrac{P(B|A_3)\cdot P(A_3)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)+ P(B|A_3)\cdot P(A_3)}$

ดังนั้น การคำนวณความน่าจะเป็นที่โทรทัศน์ที่ชำรุดคือยี่ห้อ Z จะเป็นดังนี้:

$\begin{aligned}P(A_3|B)&=\cfrac{P(B|A_3)\cdot P(A_3)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)+ P(B|A_3)\cdot P(A_3)}\\[2ex]&=\cfrac{0,04\cdot 0,30}{0,05\cdot 0,20+0,03\cdot 0,50+0,04\cdot 0,30}\\[2ex]&=0,32\end{aligned}$

โดยสรุปความน่าจะเป็นที่หากโทรทัศน์เสียเป็นยี่ห้อ Z คือ 32%

การประยุกต์ทฤษฎีบทของเบย์

มีการประยุกต์ทฤษฎีบทของเบย์ส์หลายอย่าง เช่น:

การทดสอบทางการแพทย์ : ทฤษฎีบทของเบย์ส์มักใช้ในการแพทย์เพื่อพิจารณาความน่าจะเป็นที่จะผ่านการทดสอบวินิจฉัย ตัวอย่างเช่น ในกรณีของการทดสอบ HIV ทฤษฎีบทนี้สามารถนำไปใช้ในการคำนวณความน่าจะเป็นที่บุคคลนั้นจะมีไวรัสจริงๆ หากผลการทดสอบเป็นบวก
การวิเคราะห์ทางการเงิน : ในด้านการเงิน ทฤษฎีบทของ Bayes ใช้ในการคำนวณความน่าจะเป็นที่เหตุการณ์ทางเศรษฐกิจบางอย่าง เช่น การเพิ่มขึ้นหรือลดลงของมูลค่าหุ้น จะเกิดขึ้น โดยพิจารณาจากชุดตัวแปรทางเศรษฐกิจ
การวิจัยตลาด : ทฤษฎีบทของเบย์ทำให้สามารถระบุ เช่น ความน่าจะเป็นที่บุคคลจะซื้อผลิตภัณฑ์หลังจากเห็นโฆษณาสำหรับผลิตภัณฑ์นี้
การพยากรณ์อากาศ : โมเดลสภาพอากาศยังใช้ทฤษฎีบทของเบย์ส์เพื่อกำหนดความน่าจะเป็นที่การพยากรณ์อากาศที่กำหนดตามข้อมูลที่สังเกตได้จะเป็นจริง ซึ่งจะช่วยปรับปรุงความแม่นยำของการพยากรณ์สภาพอากาศ
การรักษาความปลอดภัยของคอมพิวเตอร์ – ในโลกไซเบอร์ ทฤษฎีบทของ Bayes สามารถนำไปใช้เพื่อระบุโอกาสที่กิจกรรมที่น่าสงสัยจะเป็นการโจมตีระบบคอมพิวเตอร์อย่างแท้จริง

แก้ปัญหาทฤษฎีบทเบย์

แบบฝึกหัดที่ 1

ประมาณว่า 1% ของประชากรต้องทนทุกข์ทรมานจากโรคบางชนิด การทดสอบเพื่อตรวจหาโรคนี้มีความแม่นยำ 95% สำหรับกรณีที่เป็นบวก และ 90% สำหรับกรณีที่เป็นลบ หากสุ่มเลือกผู้มีผลตรวจเป็นบวก ความน่าจะเป็นที่พวกเขาจะเป็นโรคนี้เป็นเท่าใด

ดูวิธีแก้ปัญหา

ข้อความแบบฝึกหัดทำให้เรามีความน่าจะเป็นดังต่อไปนี้:

A ₁ : บุคคลมีโรค → P(A ₁ )=0.01
A ₂ : บุคคลไม่มีโรค → P(A ₂ )=0.99

B: ผลการทดสอบเป็นบวก
B|A ₁ : ผลบวกเมื่อผู้ป่วยเป็นโรค → P(B|A ₁ )=0.95
B|A ₂ : ผลเป็นบวกเมื่อบุคคลนั้นไม่มีโรค → P(B|A ₂ )=1-0.90=0.10

จากนั้น เพื่อคำนวณความน่าจะเป็นที่ผู้สุ่มเลือกจะเป็นโรคนี้จริงๆ เมื่อผลการทดสอบเป็นบวก กฎของเบย์จะต้องถูกนำมาใช้:

$P(A_i|B)=\cfrac{P(B|A_i)\cdot P(A_i)}{\displaystyle \sum_{k=1}^n P(B|A_k)\cdot P(A_k)}$

$P(A_1|B)=\cfrac{P(B|A_1)\cdot P(A_1)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)}$

ดังนั้นเราจึงแทนค่าลงในสูตรและทำการคำนวณความน่าจะเป็น:

$\begin{aligned}P(A_1|B)&=\cfrac{P(B|A_1)\cdot P(A_1)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)}\\[2ex]&=\cfrac{0,95\cdot 0,01}{0,95\cdot 0,01+0,10\cdot 0,99}\\[2ex]&=0,0876\end{aligned}$

กล่าวโดยสรุป ความน่าจะเป็นที่ผู้สุ่มเลือกจะมีผลตรวจเป็นบวกและเป็นโรคนี้จริงๆ คือ 8.76%

แบบฝึกหัดที่ 2

มีการประเมินว่าความน่าจะเป็นที่หุ้นจะขึ้นในหนึ่งวันคือ 40% จะยังคงทรงตัวคือ 10% และความน่าจะเป็นที่จะลดลงคือ 50% นอกจากนี้ เรารู้ว่าเมื่อตลาดสูงขึ้น มีความน่าจะเป็น 90% ที่นักวิเคราะห์ทางการเงินจะคาดการณ์ได้อย่างถูกต้อง เมื่อตลาดยังคงมีเสถียรภาพ ความน่าจะเป็นที่การคาดการณ์จะถูกต้องคือ 75% และในกรณีที่ลดลง ความน่าจะเป็นของการคาดการณ์ที่ถูกต้องคือ 75% 85%.%. หากนักวิเคราะห์คาดการณ์ว่าตลาดจะตก มีโอกาสมากน้อยเพียงใดที่ราคาจะตกจริง?

ดูวิธีแก้ปัญหา

ในกรณีนี้ ข้อความแบบฝึกหัดจะให้ความน่าจะเป็นดังต่อไปนี้:

A ₁ : ตลาดขึ้นในหนึ่งวัน → P(A ₁ )=0.40
A ₂ : ตลาดยังคงทรงตัวในหนึ่งวัน → P(A ₂ )=0.10
A ₃ : ตลาดขึ้นในหนึ่งวัน → P(A ₃ )=0.50

B: นักวิเคราะห์คาดการณ์ว่าตลาดจะตก
B|A ₁ : นักวิเคราะห์คาดการณ์ได้อย่างถูกต้องว่าตลาดจะเพิ่มขึ้น → P(B|A ₁ )=0.90
B|A ₂ : นักวิเคราะห์คาดการณ์ได้อย่างถูกต้องว่าตลาดยังคงมีเสถียรภาพ → P(B|A ₂ )=0.75
B|A ₃ : นักวิเคราะห์คาดการณ์อย่างถูกต้องว่าตลาดจะตกลง → P(B|A ₃ )=0.85

ในการพิจารณาความน่าจะเป็นที่นักวิเคราะห์คาดการณ์ว่าตลาดจะตกและถูกต้อง เราจำเป็นต้องใช้สูตรทฤษฎีบท Bayes:

$P(A_i|B)=\cfrac{P(B|A_i)\cdot P(A_i)}{\displaystyle \sum_{k=1}^n P(B|A_k)\cdot P(A_k)}$

$P(A_3|B)=\cfrac{P(B|A_3)\cdot P(A_3)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)+ P(B|A_3)\cdot P(A_3)}$

เราแทนที่ค่าความน่าจะเป็นลงในสูตรของ Bayes และคำนวณความน่าจะเป็น:

$\begin{aligned}P(A_3|B)&=\cfrac{P(B|A_3)\cdot P(A_3)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)+ P(B|A_3)\cdot P(A_3)}\\[2ex]&=\cfrac{0,85\cdot 0,50}{0,90\cdot 0,40+0,75\cdot 0,10+0,85\cdot 0,50}\\[2ex]&=0,4942\end{aligned}$

ดังนั้นความน่าจะเป็นที่นักวิเคราะห์จะพูดถูกเมื่อตลาดหุ้นจะตกคือ 49.42%

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

สวัสดี ฉันชื่อเบนจามิน ศาสตราจารย์สถิติเกษียณอายุแล้ว และผันตัวมาเป็นครูสอนสถิติโดยเฉพาะ ด้วยประสบการณ์และความเชี่ยวชาญที่กว้างขวางในสาขาสถิติ ฉันกระตือรือร้นที่จะแบ่งปันความรู้ของฉันเพื่อเสริมศักยภาพนักเรียนผ่าน Statorials. รู้เพิ่มเติม

ทฤษฎีบทของเบย์สคืออะไร?

สูตรทฤษฎีบทของเบย์

ตัวอย่างทฤษฎีบทของเบย์

การประยุกต์ทฤษฎีบทของเบย์

แก้ปัญหาทฤษฎีบทเบย์

แบบฝึกหัดที่ 1

แบบฝึกหัดที่ 2

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

เพิ่มความคิดเห็น