ทวินามเชิงลบกับปัวซอง: วิธีเลือกแบบจำลองการถดถอย

การถดถอยทวินามเชิงลบ และ การถดถอยแบบปัวซอง เป็นแบบจำลองการถดถอยสองประเภทที่ควรใช้เมื่อ ตัวแปรตอบสนอง แสดงด้วยผลลัพธ์การนับแบบไม่ต่อเนื่อง

ต่อไปนี้คือตัวอย่างบางส่วนของตัวแปรตอบสนองที่แสดงผลการนับแบบไม่ต่อเนื่อง:

• จำนวนนักศึกษาที่สำเร็จการศึกษาจากบางหลักสูตร
• จำนวนอุบัติเหตุทางถนนบริเวณทางแยกหนึ่ง
• จำนวนผู้เข้าร่วมที่เข้าเส้นชัยมาราธอน
• จำนวนการคืนสินค้าในเดือนที่กำหนดที่ร้านค้าปลีก

หากความแปรปรวนเท่ากับค่าเฉลี่ยโดยประมาณ โดยทั่วไปแล้วแบบจำลองการถดถอยปัวซองจะเหมาะกับชุดข้อมูลเป็นอย่างดี

อย่างไรก็ตาม หากความแปรปรวนมากกว่าค่าเฉลี่ยอย่างมีนัยสำคัญ โดยทั่วไปแล้วแบบจำลองการถดถอยทวินามที่เป็นลบจะสามารถใส่ข้อมูลได้ดีกว่า

มีสองเทคนิคที่เราสามารถใช้เพื่อพิจารณาว่าการถดถอยปัวซองหรือการถดถอยทวินามเชิงลบมีความเหมาะสมมากกว่าสำหรับชุดข้อมูลที่กำหนดหรือไม่:

1. แปลงที่เหลือ

เราสามารถสร้างพล็อตของปริมาณคงเหลือที่ได้มาตรฐานเทียบกับค่าที่คาดการณ์จากแบบจำลองการถดถอย

ถ้าค่าตกค้างมาตรฐานส่วนใหญ่อยู่ระหว่าง -2 ถึง 2 แบบจำลองการถดถอยปัวซองน่าจะเหมาะสม

อย่างไรก็ตาม หากส่วนที่เหลืออยู่นอกช่วงนี้ แบบจำลองการถดถอยทวินามเชิงลบน่าจะให้ความเหมาะสมที่ดีกว่า

2. การทดสอบอัตราส่วนความน่าจะเป็น

เราสามารถใส่แบบจำลองการถดถอยปัวซองและแบบจำลองการถดถอยทวินามลบเข้ากับชุดข้อมูลเดียวกัน จากนั้นจึงทำการทดสอบอัตราส่วนความน่าจะเป็น

หากค่า p ของการทดสอบต่ำกว่าระดับนัยสำคัญที่กำหนด (เช่น 0.05) เราก็สามารถสรุปได้ว่าแบบจำลองการถดถอยทวินามเชิงลบให้ความเหมาะสมที่ดีกว่าอย่างมาก

ตัวอย่างต่อไปนี้แสดงวิธีใช้เทคนิคทั้งสองนี้ใน R เพื่อพิจารณาว่าควรใช้แบบจำลองการถดถอยปัวซองหรือแบบจำลองการถดถอยทวินามเชิงลบสำหรับชุดข้อมูลที่กำหนด

ตัวอย่าง: การถดถอยทวินามเชิงลบเทียบกับการถดถอยปัวซอง

สมมติว่าเราต้องการทราบว่านักเบสบอลระดับมัธยมปลายในเขตที่กำหนดได้รับทุนการศึกษาจำนวนเท่าใด โดยพิจารณาจากแผนกการเรียนของเขา (“A”, “B” หรือ “C”) และเกรดของโรงเรียน การสอบเข้ามหาวิทยาลัย (วัดจาก 0 ถึง 100) ).

ใช้ขั้นตอนต่อไปนี้เพื่อพิจารณาว่าแบบจำลองการถดถอยทวินามลบหรือแบบจำลองการถดถอยปัวซองเหมาะสมกับข้อมูลมากกว่าหรือไม่

ขั้นตอนที่ 1: สร้างข้อมูล

โค้ดต่อไปนี้จะสร้างชุดข้อมูลที่เราจะร่วมงานด้วย ซึ่งรวมถึงข้อมูลเกี่ยวกับผู้เล่นเบสบอล 1,000 คน:

 #make this example reproducible
set. seeds (1)

#create dataset
data <- data. frame (offers = c(rep(0, 700), rep(1, 100), rep(2, 100),
                              rep(3, 70), rep(4, 30)),
                   division = sample(c(' A ', ' B ', ' C '), 100, replace = TRUE ),
                   exam = c(runif(700, 60, 90), runif(100, 65, 95),
                            runif(200, 75, 95)))

#view first six rows of dataset
head(data)

  offers division exam
1 0 A 66.22635
2 0 C 66.85974
3 0 A 77.87136
4 0 B 77.24617
5 0 A 62.31193
6 0 C 61.06622

ขั้นตอนที่ 2: ติดตั้งแบบจำลองการถดถอยปัวซองและแบบจำลองการถดถอยทวินามที่เป็นลบ

รหัสต่อไปนี้แสดงวิธีปรับทั้งแบบจำลองการถดถอยปัวซองและแบบจำลองการถดถอยทวินามลบให้กับข้อมูล:

 #fit Poisson regression model
p_model <- glm(offers ~ division + exam, family = ' fish ', data = data)

#fit negative binomial regression model
library (MASS)

nb_model <- glm. nb (offers ~ division + exam, data = data)

ขั้นตอนที่ 3: สร้างแปลงที่เหลือ

รหัสต่อไปนี้แสดงวิธีสร้างแปลงที่เหลือสำหรับทั้งสองรุ่น

 #Residual plot for Poisson regression
p_res <- resid (p_model)
plot(fitted(p_model), p_res, col=' steelblue ', pch=16,
     xlab=' Predicted Offers ', ylab=' Standardized Residuals ', main=' Poisson ')
abline(0,0)

#Residual plot for negative binomial regression
nb_res <- resid (nb_model)
plot(fitted(nb_model), nb_res, col=' steelblue ', pch=16,
     xlab=' Predicted Offers ', ylab=' Standardized Residuals ', main=' Negative Binomial ')
abline(0,0) 

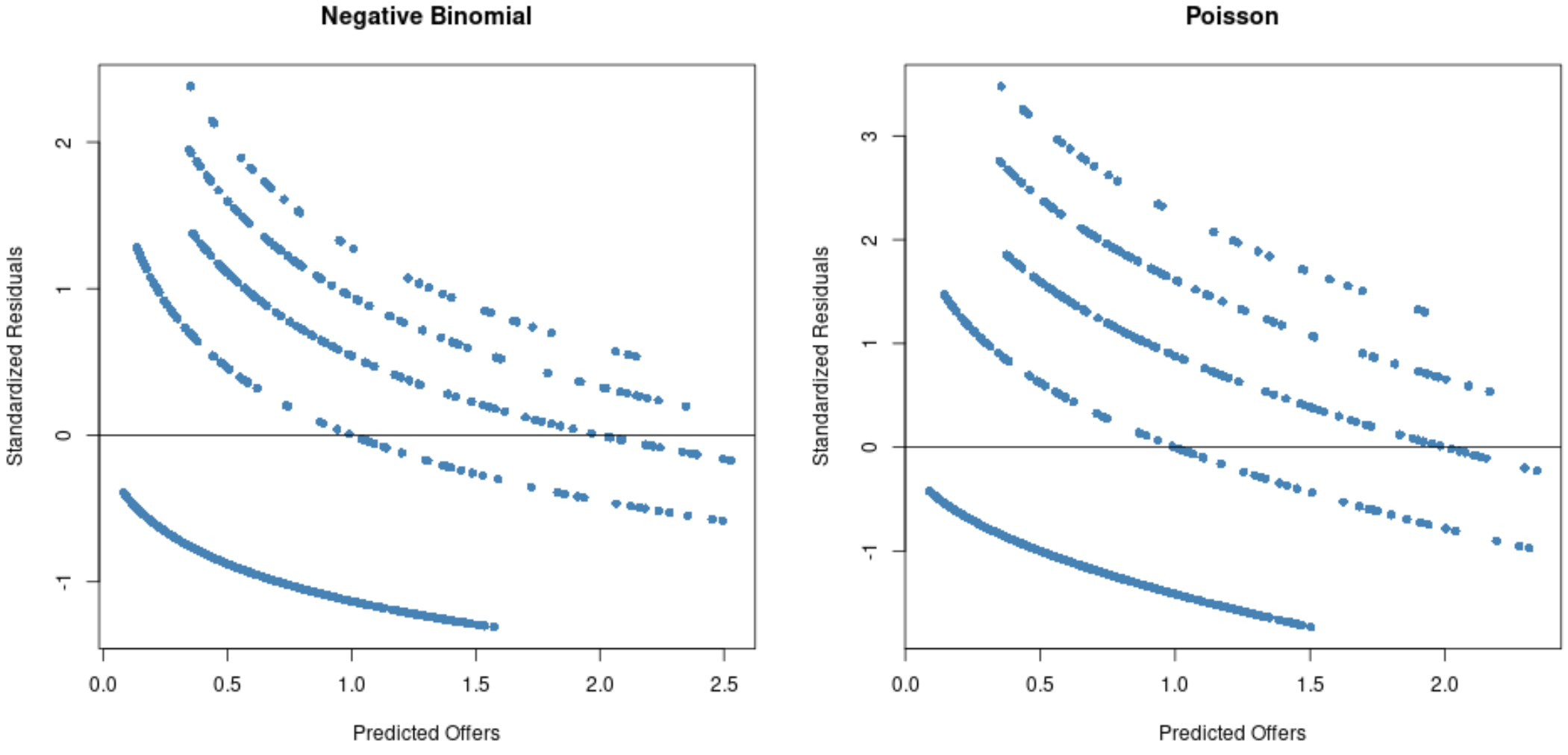
จากกราฟ เราจะเห็นว่าส่วนที่เหลือจะกระจายออกไปมากขึ้นสำหรับแบบจำลองการถดถอยปัวซอง (โปรดทราบว่าส่วนที่เหลือบางส่วนขยายเกิน 3) เมื่อเปรียบเทียบกับแบบจำลองการถดถอยทวินามเชิงลบ

นี่เป็นสัญญาณว่าแบบจำลองการถดถอยทวินามลบน่าจะเหมาะสมกว่าเนื่องจากส่วนที่เหลือของแบบจำลองนี้มีขนาดเล็กกว่า

ขั้นตอนที่ 4: ทำการทดสอบอัตราส่วนความน่าจะเป็น

สุดท้ายนี้ เราสามารถทำการทดสอบอัตราส่วนความน่าจะเป็นเพื่อพิจารณาว่ามีความแตกต่างที่มีนัยสำคัญทางสถิติในแบบจำลองการถดถอยทั้งสองแบบหรือไม่:

 pchisq(2 * ( logLik (nb_model) - logLik (p_model)), df = 1, lower. tail = FALSE )

'log Lik.' 3.508072e-29 (df=5)

ค่า p ของการทดสอบกลายเป็น 3.508072e-29 ซึ่งน้อยกว่า 0.05 อย่างมีนัยสำคัญ

ดังนั้น เราจะสรุปได้ว่าแบบจำลองการถดถอยแบบทวินามลบนั้นมีความเหมาะสมกับข้อมูลที่ดีกว่าอย่างมากเมื่อเทียบกับแบบจำลองการถดถอยแบบปัวซอง

แหล่งข้อมูลเพิ่มเติม

ความรู้เบื้องต้นเกี่ยวกับการแจกแจงแบบทวินามลบ
ความรู้เบื้องต้นเกี่ยวกับการกระจายปัวซอง