วิธีการดำเนินการวิเคราะห์ความแปรปรวนแบบทางเดียวใน spss

การวิเคราะห์ความแปรปรวนแบบทางเดียว ใช้เพื่อพิจารณาว่ามีความแตกต่างที่มีนัยสำคัญทางสถิติระหว่างค่าเฉลี่ยของกลุ่มอิสระสามกลุ่มขึ้นไปหรือไม่

การทดสอบประเภทนี้เรียกว่าการวิเคราะห์ความแปรปรวนแบบทางเดียว เนื่องจากเราวิเคราะห์ผลกระทบ ของ ตัวแปรทำนายต่อตัวแปรตอบสนอง

หากเราสนใจผลกระทบ ของตัวแปรทำนายสองตัว ที่มีต่อตัวแปรตอบสนองแทน เราก็สามารถดำเนิน การวิเคราะห์ความแปรปรวนแบบสองทางได้

บทช่วยสอนนี้จะอธิบายวิธีการดำเนินการวิเคราะห์ความแปรปรวนแบบทางเดียวใน SPSS

ตัวอย่าง: การวิเคราะห์ความแปรปรวนแบบทางเดียวใน SPSS

สมมติว่านักวิจัยรับสมัครนักศึกษาจำนวน 30 คนเพื่อเข้าร่วมการศึกษาวิจัย นักเรียนจะถูกสุ่มให้ใช้หนึ่งในสามเทคนิคการเรียนในเดือนถัดไปเพื่อเตรียมตัวสอบ สิ้นเดือน นักเรียนทุกคนจะสอบแบบเดียวกัน

ผลการทดสอบของนักเรียนแสดงไว้ด้านล่าง:

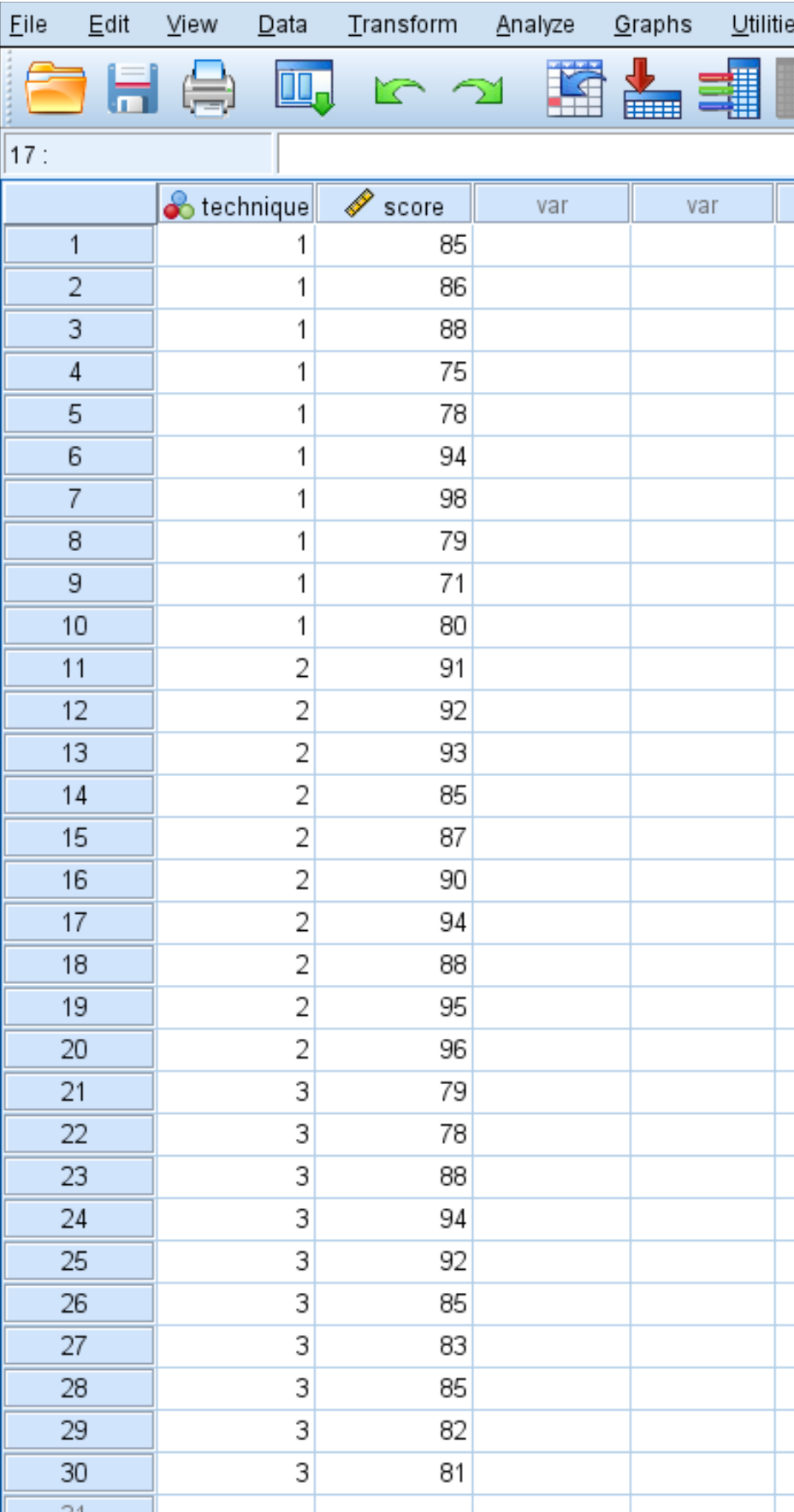
ใช้ขั้นตอนต่อไปนี้เพื่อทำการวิเคราะห์ความแปรปรวนแบบทางเดียวเพื่อพิจารณาว่าคะแนนเฉลี่ยเท่ากันในทั้งสามกลุ่มหรือไม่

ขั้นตอนที่ 1: แสดงภาพข้อมูล

ขั้นแรก เราจะสร้าง Boxplots เพื่อแสดงภาพการกระจายคะแนนการทดสอบสำหรับเทคนิคการศึกษาแต่ละเทคนิคจากทั้งสามเทคนิค คลิกแท็บ แผนภูมิ จากนั้นคลิก ตัวสร้างแผนภูมิ

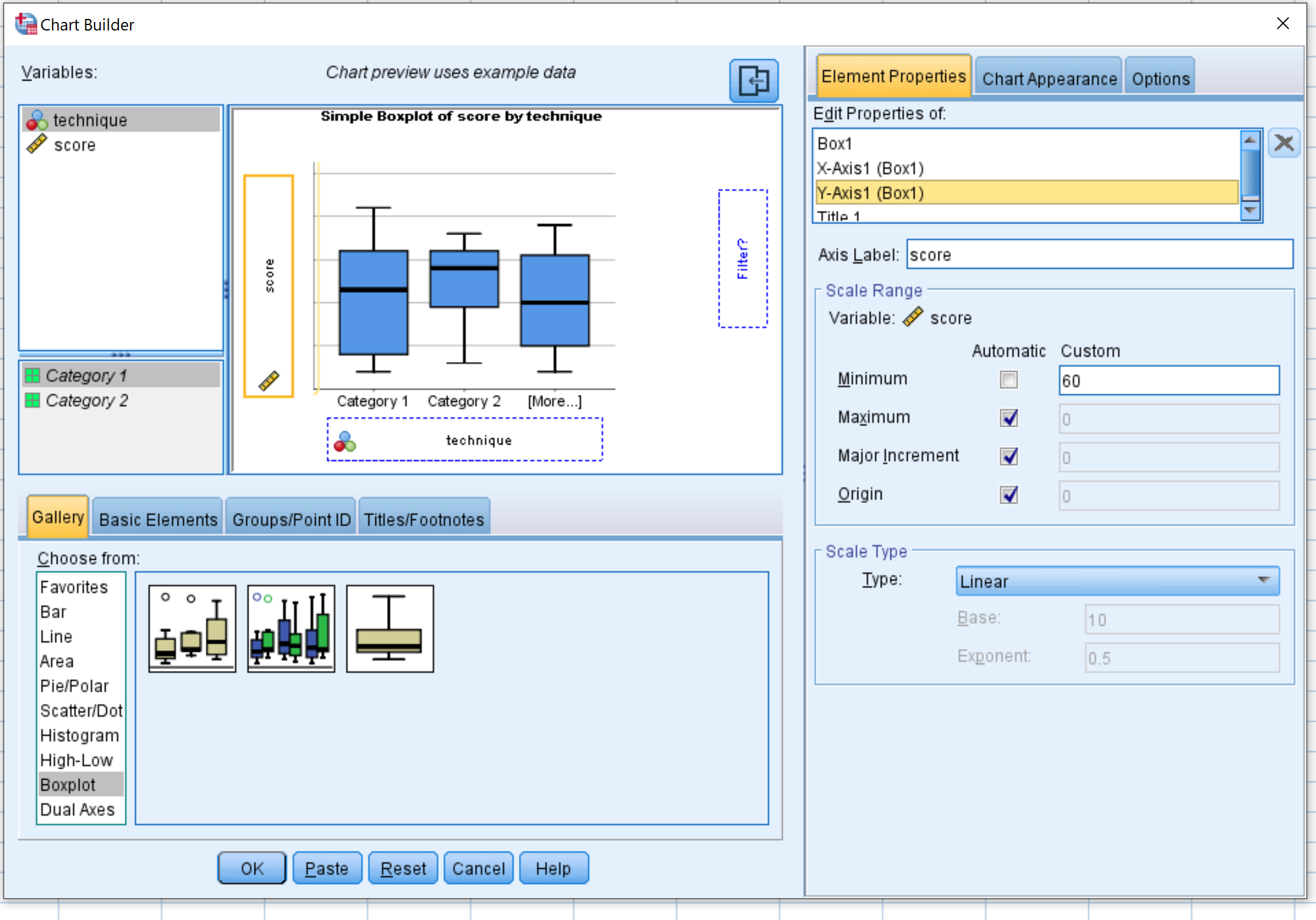
เลือก Boxplot ในหน้าต่าง เลือกจาก: จากนั้นลากแผนภูมิแรกที่มีชื่อว่า Simple boxplot ลงในหน้าต่างแก้ไขหลัก ลากตัวแปร ทางเทคนิค บนแกน x และ ลากคะแนน บนแกน y

จากนั้นคลิก คุณสมบัติองค์ประกอบ จากนั้น คลิก แกน Y1 เปลี่ยนค่า ต่ำสุด เป็น 60 จากนั้นคลิก ตกลง

Boxplots ต่อไปนี้จะปรากฏขึ้น:

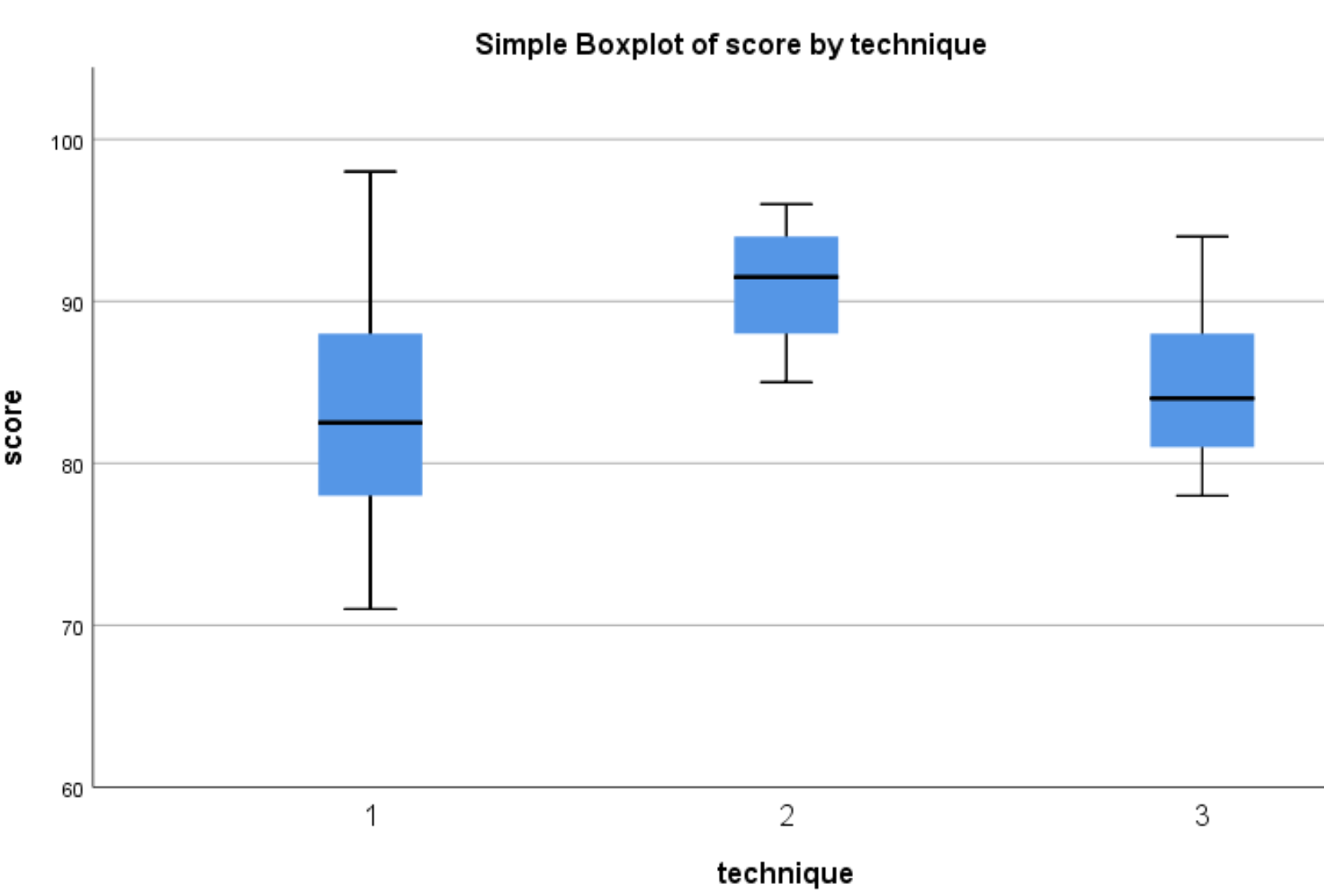
เราจะเห็นได้ว่าการกระจายของคะแนนทดสอบมีแนวโน้มที่จะสูงกว่าสำหรับนักเรียนที่ใช้เทคนิค 2 มากกว่านักเรียนที่ใช้เทคนิค 1 และ 3 เพื่อพิจารณาว่าความแตกต่างของคะแนนเหล่านี้มีนัยสำคัญทางสถิติหรือไม่ เราจะดำเนินการวิเคราะห์ความแปรปรวนแบบทางเดียว

ขั้นตอนที่ 2: ดำเนินการวิเคราะห์ความแปรปรวนแบบทางเดียว

คลิกแท็บ วิเคราะห์ จากนั้น เปรียบเทียบค่าเฉลี่ย จากนั้นคลิก การวิเคราะห์ความแปรปรวนแบบทางเดียว

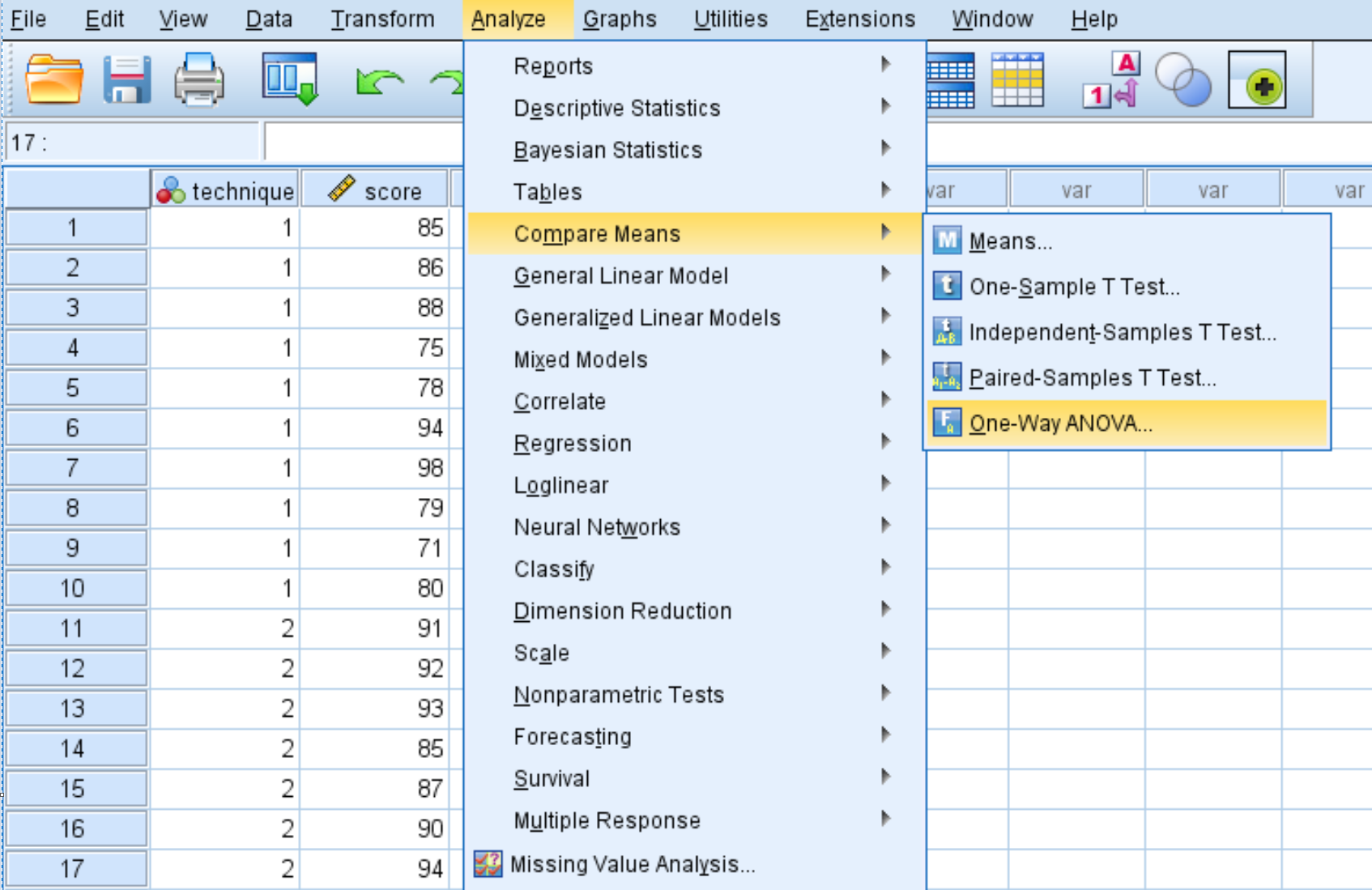
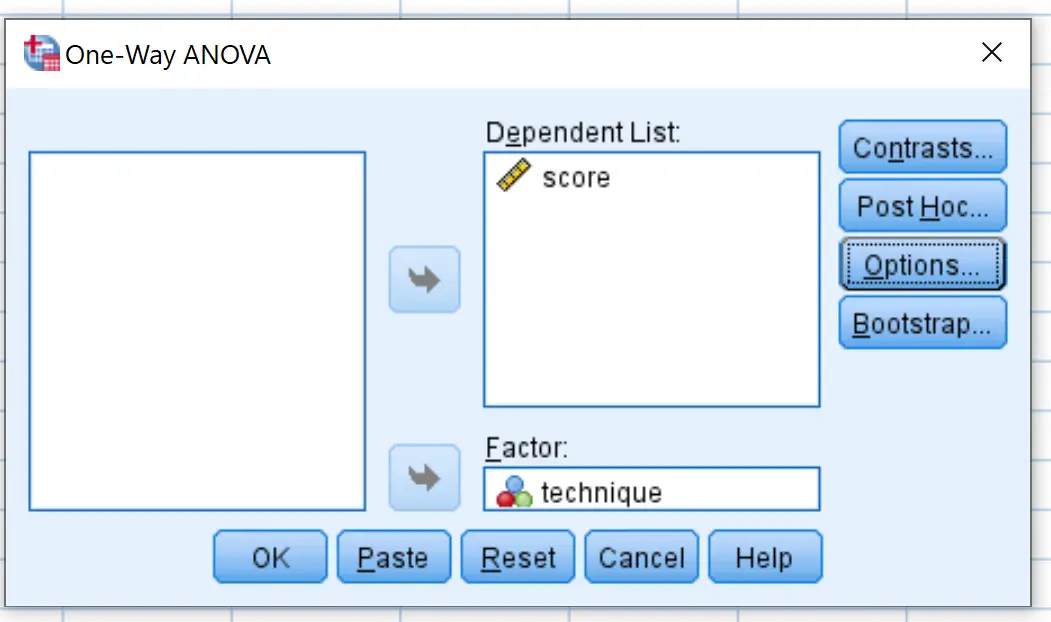
ในหน้าต่างใหม่ที่ปรากฏขึ้น ให้วาง คะแนน ตัวแปรในกล่องที่มีข้อความว่า Dependent List และ เทคนิค ตัวแปรในกล่องที่มีข้อความว่า Factor

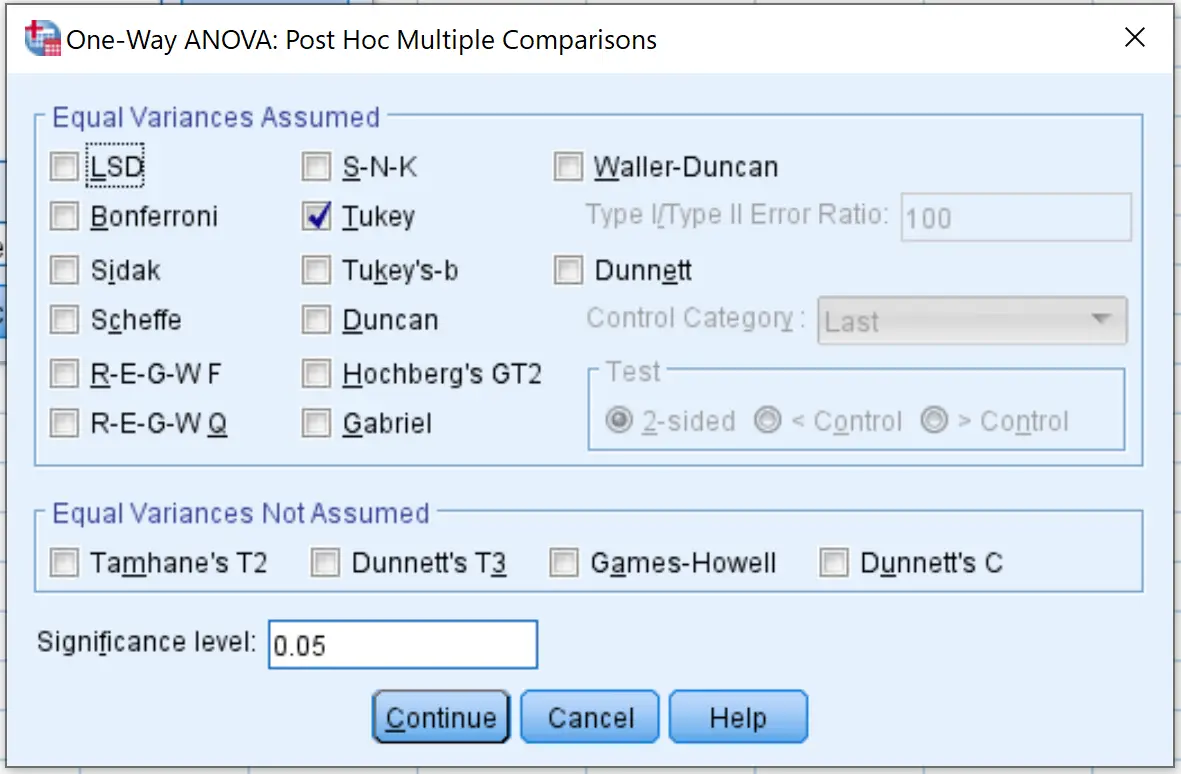
จากนั้นคลิก Post Hoc และทำเครื่องหมายที่ช่องถัดจาก Tukey จากนั้นคลิก ดำเนินการต่อ

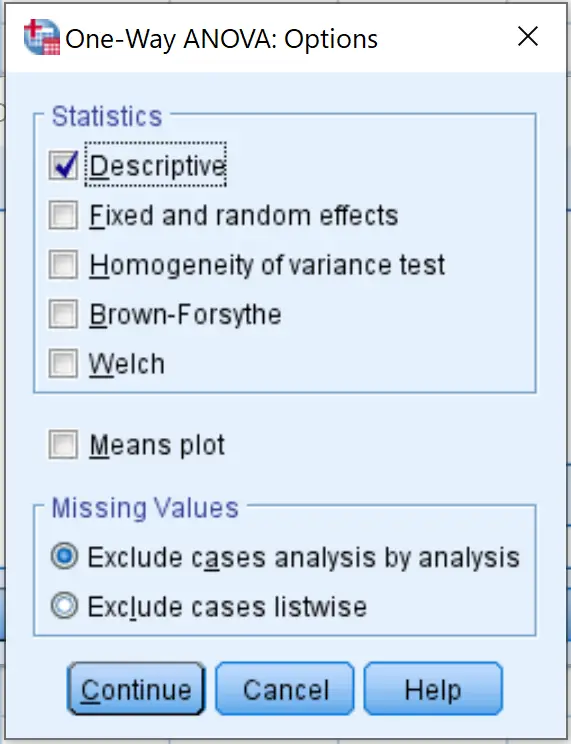
จากนั้นคลิก ตัวเลือก และทำเครื่องหมายในช่องถัดจาก คำอธิบาย จากนั้นคลิก ดำเนินการต่อ

สุดท้ายคลิก ตกลง

ขั้นตอนที่ 3: ตีความผลลัพธ์

เมื่อคุณคลิก ตกลง ผลลัพธ์ ANOVA แบบทางเดียวจะปรากฏขึ้น ต่อไปนี้เป็นวิธีการตีความผลลัพธ์:

คำอธิบายตาราง

ตารางนี้แสดงสถิติเชิงพรรณนาสำหรับแต่ละกลุ่มจากสามกลุ่มในชุดข้อมูลของเรา

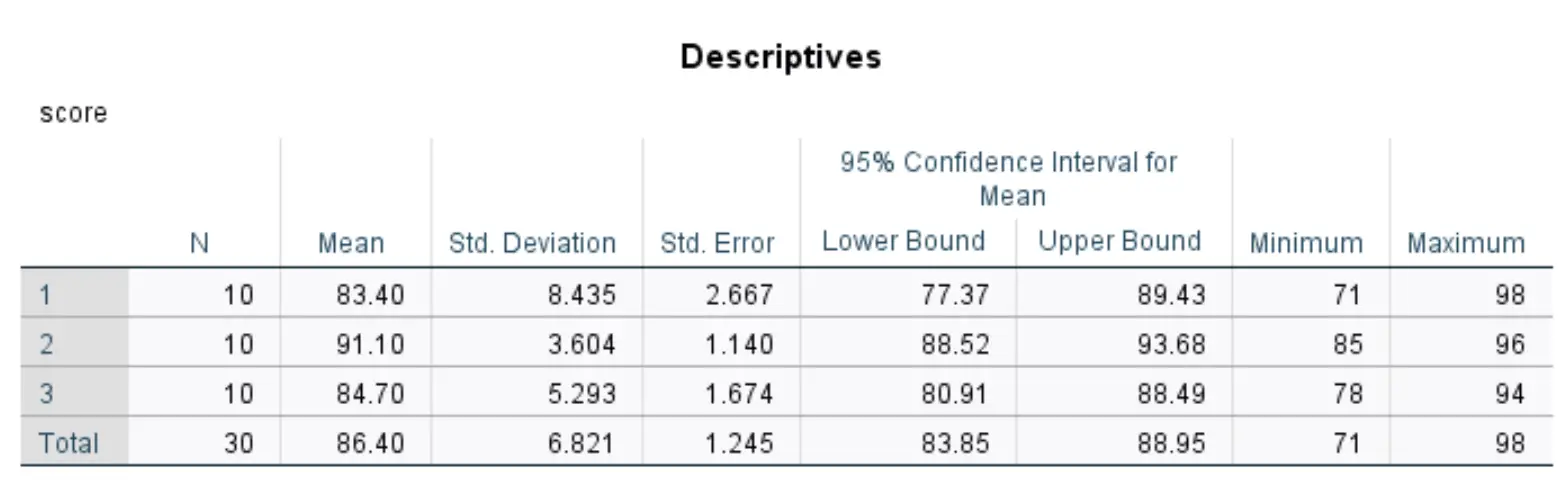
ตัวเลขที่เกี่ยวข้องมากที่สุด ได้แก่:

• N: จำนวนนักเรียนในแต่ละกลุ่ม
• เฉลี่ย: คะแนนสอบเฉลี่ยของแต่ละกลุ่ม
• มาตรฐาน. ส่วนเบี่ยงเบน: ส่วนเบี่ยงเบนมาตรฐานของผลการทดสอบสำหรับแต่ละกลุ่ม

ตารางความแปรปรวน

ตารางนี้แสดงผลลัพธ์ของการวิเคราะห์ความแปรปรวนแบบทางเดียว:

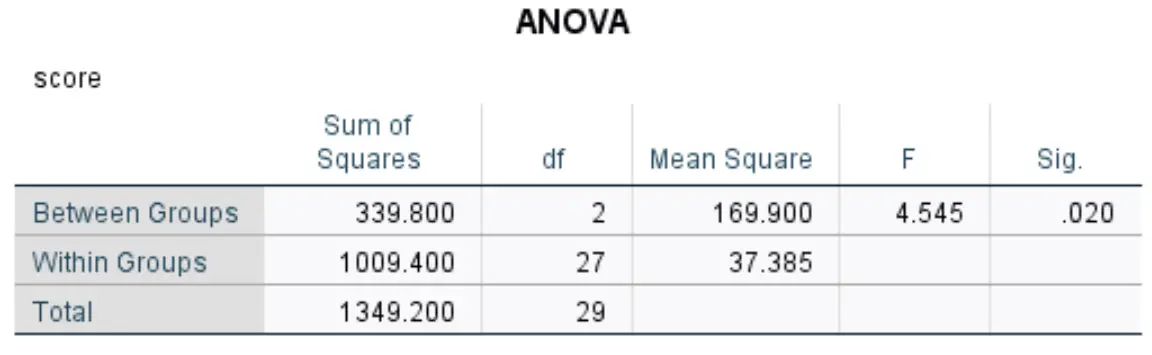
ตัวเลขที่เกี่ยวข้องมากที่สุด ได้แก่:

• F: สถิติ F โดยรวม
• Sig: ค่า p ซึ่งสอดคล้องกับสถิติ F (4.545) โดยมีตัวเศษ df (2) และตัวส่วน df (27) ในกรณีนี้ ค่า p จะกลายเป็น 0.020

โปรดจำไว้ว่าการวิเคราะห์ความแปรปรวนทางเดียวใช้สมมติฐานว่างและทางเลือกต่อไปนี้:

• H ₀ (สมมติฐานว่าง): μ ₁ = μ ₂ = μ ₃ = … = μ _k (ค่าเฉลี่ยประชากรทั้งหมดเท่ากัน)
• H _A (สมมติฐานทางเลือก): ค่าเฉลี่ยประชากรอย่างน้อย 1 รายการแตกต่างกัน   พักผ่อน

เนื่องจากค่า p ของตาราง ANOVA น้อยกว่า 0.05 เราจึงมีหลักฐานเพียงพอที่จะปฏิเสธสมมติฐานว่างและสรุปได้ว่าค่าเฉลี่ยของกลุ่มอย่างน้อยหนึ่งรายการแตกต่างจากค่าเฉลี่ยอื่นๆ

หากต้องการทราบว่าค่าเฉลี่ยของกลุ่มใดที่แตกต่างกัน เราสามารถดูตารางสุดท้ายของผลลัพธ์ ANOVA ได้

ตารางเปรียบเทียบหลายรายการ

ตารางนี้แสดงการเปรียบเทียบหลายรายการหลังการดำเนินการของ Tukey ระหว่างแต่ละกลุ่มจากสามกลุ่ม เราสนใจ Sig เป็นหลัก คอลัมน์ซึ่งแสดงค่า p สำหรับความแตกต่างในค่าเฉลี่ยระหว่างแต่ละกลุ่ม:

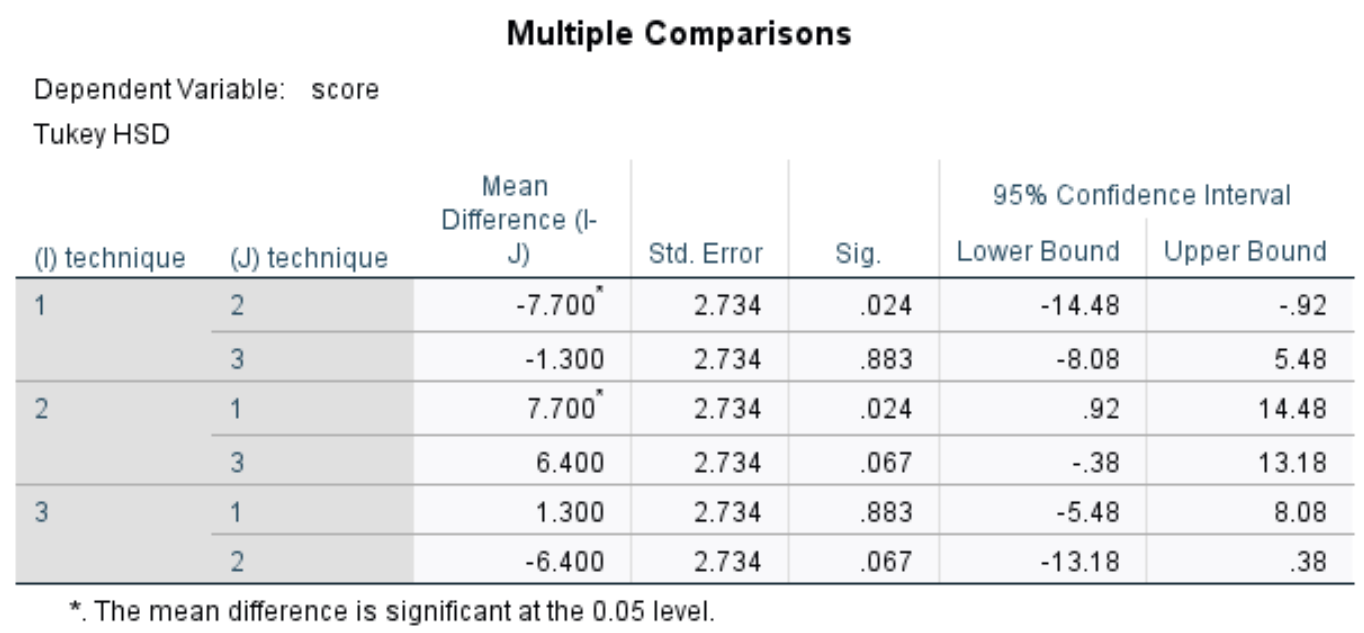
ในตารางเราจะเห็นค่า p สำหรับการเปรียบเทียบต่อไปนี้:

• เทคนิค 1 ต่อ 2: | ค่า p = 0.024
• เทคนิค 1 ต่อ 3 | ค่า p = 0.883
• เทคนิค 2 ต่อ 3 | ค่า p = 0.067

การเปรียบเทียบกลุ่มเดียวที่มีค่า p น้อยกว่า 0.05 คือระหว่างเทคนิคที่ 1 และเทคนิคที่ 2

สิ่งนี้บอกเราว่าคะแนนการทดสอบเฉลี่ยระหว่างนักเรียนที่ใช้เทคนิคที่ 1 และผู้ที่ใช้เทคนิคที่ 2 มีความแตกต่างอย่างมีนัยสำคัญทางสถิติ

อย่างไรก็ตาม ไม่มีความแตกต่างที่มีนัยสำคัญทางสถิติระหว่างเทคนิค 1 และ 3 หรือระหว่างเทคนิค 2 และ 3

ขั้นตอนที่ 4: รายงานผลลัพธ์

สุดท้ายนี้ เราสามารถรายงานผลลัพธ์ของการวิเคราะห์ความแปรปรวนแบบทางเดียวได้ นี่คือตัวอย่างของวิธีการทำเช่นนี้:

มีการดำเนินการวิเคราะห์ความแปรปรวนแบบทางเดียวเพื่อตรวจสอบว่าเทคนิคการศึกษาที่แตกต่างกันสามเทคนิคนำไปสู่ผลการทดสอบที่แตกต่างกันหรือไม่

นักเรียนทั้งหมด 10 คนใช้เทคนิคการเรียนทั้งสามแบบเป็นเวลาหนึ่งเดือนก่อนจะสอบแบบเดียวกันทั้งหมด

การวิเคราะห์ความแปรปรวนแบบทางเดียวเปิดเผยว่ามีความแตกต่างที่มีนัยสำคัญทางสถิติในคะแนนการทดสอบระหว่างอย่างน้อยสองกลุ่ม (F(2, 27) = 4.545, p = 0.020)

การทดสอบของ Tukey สำหรับการเปรียบเทียบหลายรายการพบว่าคะแนนการทดสอบเฉลี่ยแตกต่างกันอย่างมีนัยสำคัญระหว่างนักเรียนที่ใช้เทคนิคที่ 1 และเทคนิคที่ 2 (p = 0.024, 95% CI = [-14.48, -0.92])

ไม่มีความแตกต่างที่มีนัยสำคัญทางสถิติระหว่างคะแนนสำหรับเทคนิค 1 และ 3 (p = 0.883) หรือระหว่างคะแนนสำหรับเทคนิค 2 และ 3 (p = 0.067)