แบบทดสอบของนักเรียน

โดย ดร.เบนจามิน แอนเดอร์สัน สิงหาคม 3, 2023 สถิติ 0 ความคิดเห็น

บทความนี้จะอธิบายว่า Student t test คืออะไร และใช้เพื่ออะไรในสถิติ ดังนั้น คุณจะค้นพบว่าการทดสอบของนักเรียนดำเนินการอย่างไร การทดสอบของนักเรียนประเภทต่างๆ มีอะไรบ้าง และสูตรสำหรับแต่ละรายการ

t-test ของนักเรียนคืออะไร?

การทดสอบทีของนักเรียน หรือเรียกอีกอย่างว่า การทดสอบที หรือเรียกง่ายๆ ว่า การทดสอบที คือการทดสอบทางสถิติซึ่งสถิติการทดสอบจะเป็นไปตาม การแจกแจงค่า t ของนักเรียน ดังนั้น ในทางสถิติ การทดสอบทีของนักเรียนใช้เพื่อปฏิเสธหรือยอมรับสมมติฐานว่างของการทดสอบสมมติฐาน

โดยเฉพาะอย่างยิ่ง การทดสอบทีของนักเรียนใช้ใน การทดสอบสมมติฐาน ซึ่งประชากรที่กำลังศึกษาเป็นไปตามการแจกแจงแบบปกติ แต่ขนาดของกลุ่มตัวอย่างน้อยเกินกว่าจะทราบความแปรปรวนของประชากร

กล่าวโดยสรุป การทดสอบของนักเรียนใช้เพื่อปฏิเสธหรือยอมรับสมมติฐานการศึกษาของการทดสอบสมมติฐานบางอย่าง ตัวอย่างเช่น การทดสอบทีของนักเรียนใช้เพื่อทดสอบสมมติฐานสำหรับหนึ่งตัวอย่าง สำหรับตัวอย่างอิสระ หรือสำหรับตัวอย่างที่เกี่ยวข้อง จากนั้นเราจะดูว่าการทดสอบของนักเรียนมีการคำนวณอย่างไรในแต่ละกรณี

ประเภทของการทดสอบทีของนักเรียน

การทดสอบของนักเรียนมีสามประเภท :

การทดสอบทีของนักเรียนตัวอย่างหนึ่งรายการ – ใช้เพื่อทดสอบสมมติฐานเกี่ยวกับค่าของค่าเฉลี่ยตัวอย่าง
การทดสอบของนักเรียนสำหรับตัวอย่างอิสระสองตัวอย่าง : ช่วยให้คุณสามารถทดสอบสมมติฐานเกี่ยวกับความแตกต่างระหว่างค่าเฉลี่ยของกลุ่มตัวอย่างอิสระสองตัวอย่าง
การทดสอบทีของนักเรียนสำหรับตัวอย่างที่จับคู่สองตัวอย่าง (หรือตัวอย่างที่เกี่ยวข้อง) – ใช้ในการตรวจสอบสมมติฐานเกี่ยวกับค่าเฉลี่ยของกลุ่มตัวอย่างที่ทดสอบสองครั้ง

ตัวอย่างข้อสอบของนักเรียน

การทดสอบสมมติฐานสำหรับค่าเฉลี่ยตัวอย่างคือการทดสอบที่สมมติฐานว่างและสมมติฐานทางเลือกของการทดสอบบอกอะไรบางอย่างเกี่ยวกับค่าของค่าเฉลี่ยประชากร

สูตรสำหรับการทดสอบ Student t แบบตัวอย่างเดียว มีดังนี้:

$\displaystyle t=\frac{\overline{x}-\mu}{\displaystyle \frac{s}{\sqrt{n}}}$

ทอง:

$t$

คือสถิติการทดสอบสมมติฐานสำหรับค่าเฉลี่ย ซึ่งกำหนดโดยการแจกแจงค่า t ของนักเรียน
$\overline{x}$

คือค่าเฉลี่ยตัวอย่าง
$\mu$

คือค่ากลางที่เสนอในการทดสอบสมมติฐาน
$s$

คือค่าเบี่ยงเบนมาตรฐานตัวอย่าง
$n$

คือขนาดตัวอย่าง

เมื่อคำนวณค่าการทดสอบ t ของนักเรียนแล้ว ผลลัพธ์ของการทดสอบทางสถิติที่มีค่าวิกฤตจะต้องถูกตีความเพื่อปฏิเสธหรือไม่ยอมรับสมมติฐานว่าง:

หากการทดสอบสมมติฐานสำหรับค่าเฉลี่ยเป็นแบบสองด้าน สมมติฐานว่างจะถูกปฏิเสธหากค่าสัมบูรณ์ของการทดสอบของนักเรียนมากกว่าค่าวิกฤต t _α/2|n-1
หากการทดสอบสมมติฐานสำหรับค่าเฉลี่ยตรงกับหางด้านขวา สมมติฐานว่างจะถูกปฏิเสธหากค่าการทดสอบทีของนักเรียนมากกว่าค่าวิกฤต t _α|n-1
หากการทดสอบสมมติฐานสำหรับค่าเฉลี่ยตรงกับหางซ้าย สมมติฐานว่างจะถูกปฏิเสธหากค่าการทดสอบทีของนักเรียนน้อยกว่าค่าวิกฤต -t _α|n-1

$\begin{array}{l}H_1: \mu\neq \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |t|>t_{\alpha/2|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu> \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t>t_{\alpha|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu< \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t<-t_{\alpha|n-1} \text{ se rechaza } H_0\end{array}$

โปรดทราบว่าค่าการทดสอบวิกฤตนั้นได้มาจากตารางการแจกแจงของนักเรียน

➤ ดู: ตัวอย่างที่เป็นรูปธรรมของการทดสอบสมมติฐานสำหรับค่าเฉลี่ย

การทดสอบของนักเรียนสำหรับตัวอย่างอิสระ

การทดสอบทีของนักเรียนสำหรับกลุ่มตัวอย่างอิสระใช้เพื่อปฏิเสธหรือยอมรับสมมติฐานของความสัมพันธ์ระหว่างค่าเฉลี่ยของประชากรทั้งสอง ตัวอย่างเช่น ค่าเฉลี่ยของประชากรทั้งสองแตกต่างกัน หรือค่าเฉลี่ยของประชากร A มากกว่าค่าเฉลี่ยของ . ประชากร บี

อย่างไรก็ตาม ในกรณีนี้ สูตรการทดสอบทีของนักเรียนจะแตกต่างกันไป ขึ้นอยู่กับว่าความแปรปรวนของประชากรสามารถสันนิษฐานได้ว่าเท่ากันหรือไม่ จากนั้นเราจะเห็นสองกรณีที่เป็นไปได้

การเบี่ยงเบนที่ไม่รู้จักและเท่ากัน

สูตรในการคำนวณการทดสอบ Student t สำหรับตัวอย่างอิสระเมื่อไม่ทราบความแปรปรวนของประชากรแต่ถือว่าเท่ากันมี ดังนี้

$\displaystyle t=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}$

ทอง:

$t$

เป็นสถิติการทดสอบสมมติฐานสำหรับผลต่างของค่าเฉลี่ยโดยไม่ทราบความแปรปรวน ซึ่งเป็นไปตามการแจกแจงค่า t ของนักเรียนที่มีดีกรีอิสระ n ₁ + n ₂ -2
$\mu_1$

คือค่าเฉลี่ยของประชากร 1
$\mu_2$

คือค่าเฉลี่ยของประชากร 2
$\overline{x_1}$

คือค่าเฉลี่ยของกลุ่มตัวอย่างที่ 1
$\overline{x_2}$

คือค่าเฉลี่ยของกลุ่มตัวอย่างที่ 2
$s_p$

คือค่าเบี่ยงเบนมาตรฐานรวม
$n_1$

คือขนาดตัวอย่างที่ 1
$n_2$

คือขนาดตัวอย่างที่ 2

ค่าเบี่ยงเบนมาตรฐานรวมของทั้งสองตัวอย่างคำนวณโดยใช้สูตรต่อไปนี้:

$\displaystyle s_p=\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}$

รูปแบบที่ไม่รู้จักและแตกต่างกัน

เมื่อไม่ทราบความแปรปรวนของประชากรและสันนิษฐานว่าแตกต่างกัน สูตรในการคำนวณการทดสอบของนักเรียนสำหรับตัวอย่างอิสระ จะเป็นดังนี้:

$\displaystyle t=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle \sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}}$

ทอง:

$t$

เป็นสถิติการทดสอบสมมติฐานสำหรับผลต่างของค่าเฉลี่ยโดยไม่ทราบความแปรปรวน ซึ่งเป็นไปตามการแจกแจงค่า t ของนักเรียน
$\mu_1$

คือค่าเฉลี่ยของประชากร 1
$\mu_2$

คือค่าเฉลี่ยของประชากร 2
$\overline{x_1}$

คือค่าเฉลี่ยของกลุ่มตัวอย่างที่ 1
$\overline{x_2}$

คือค่าเฉลี่ยของกลุ่มตัวอย่างที่ 2
$\sigma_1$

คือค่าเบี่ยงเบนมาตรฐานของประชากร 1
$\sigma_2$

คือค่าเบี่ยงเบนมาตรฐานของประชากร 2
$n_1$

คือขนาดตัวอย่างที่ 1
$n_2$

คือขนาดตัวอย่างที่ 2

อย่างไรก็ตาม ในกรณีนี้ องศาอิสระของการแจกแจง t ของนักเรียนคำนวณโดยใช้สูตรต่อไปนี้:

$\displaystyle GL=\frac{\displaystyle\left(\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}\right)^2}{\displaystyle\frac{\displaystyle\frac{s_1^2}{n_1}}{n_1-1}+\frac{\displaystyle\frac{s_2^2}{n_2}}{n_2-1}}$

➤ ดู: ตัวอย่างที่เป็นรูปธรรมของการทดสอบสมมติฐานสำหรับความแตกต่างในค่าเฉลี่ย

การทดสอบของนักเรียนสำหรับตัวอย่างที่จับคู่หรือเกี่ยวข้อง

การทดสอบนี้ใช้เมื่อตัวอย่างสองตัวอย่างที่กำลังศึกษามีความสัมพันธ์กัน เพื่อให้เป็นตัวอย่างเดียวของบุคคลที่ได้รับการวิเคราะห์สองครั้ง (ในแต่ละครั้งภายใต้เงื่อนไขที่ต่างกัน)

ตัวอย่างเช่น คุณสามารถวิเคราะห์ผลการเรียนของนักเรียนในหลักสูตรคณิตศาสตร์และสถิติเพื่อดูว่าค่าเฉลี่ยของทั้งสองวิชามีความแตกต่างกันอย่างมีนัยสำคัญหรือไม่ ในกรณีนี้ เกรดคณิตศาสตร์ของนักเรียนแต่ละคนจะเชื่อมโยงกับเกรดสถิติของนักเรียนคนเดียวกัน

สูตรการทดสอบทีของนักเรียนสำหรับตัวอย่างที่จับคู่หรือเกี่ยวข้อง คือ:

$\displaystyle t=\frac{\overline{x_D}-\mu_D}{\displaystyle \frac{s_D}{\sqrt{n}}}$

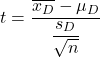
ทอง:

$t$

คือสถิติการทดสอบสมมติฐานสำหรับค่าเฉลี่ยคู่ ซึ่งกำหนดโดยการแจกแจงค่า t ของนักเรียน
$\overline{x_D}$

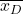
คือค่าเฉลี่ยของกลุ่มตัวอย่างที่เกิดจากผลต่างของข้อมูล
$\mu_D$

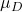
คือค่ากลางที่เสนอในการทดสอบสมมติฐาน
$s_D$

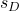
คือค่าเบี่ยงเบนมาตรฐานของกลุ่มตัวอย่างที่เกิดจากผลต่างของข้อมูล
$n$

คือขนาดตัวอย่าง

สมมติฐานการทดสอบทีของนักเรียน

เพื่อที่จะทำแบบทดสอบของนักเรียน จะต้องเป็นไปตามเงื่อนไขต่อไปนี้:

ความต่อเนื่อง – ข้อมูลตัวอย่างมีความต่อเนื่อง
ความสุ่ม : ตัวอย่างข้อมูลถูกเลือกแบบสุ่ม
ความสม่ำเสมอ : ความแปรปรวนของตัวอย่างข้อมูลเป็นเนื้อเดียวกัน
ความปกติ – การกระจายที่กำหนดตัวอย่างข้อมูลจะอยู่ที่ประมาณปกติ

วิธีทำแบบทดสอบของนักเรียน

โดยสรุป ขั้นตอนในการดำเนินการทดสอบของนักเรียนมีรายละเอียดครบถ้วน

กำหนด สมมติฐานว่างและทางเลือก ของการทดสอบสมมติฐาน
กำหนด ระดับนัยสำคัญ (α) ของการทดสอบสมมติฐาน
ตรวจสอบว่าเป็นไปตามสมมติฐานของการทดสอบของนักเรียน
ใช้สูตรการทดสอบทีของนักเรียนที่เกี่ยวข้องและคำนวณสถิติการทดสอบ
ตีความผลการทดสอบของนักเรียนโดยเปรียบเทียบกับค่าวิกฤตของการทดสอบ

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

สวัสดี ฉันชื่อเบนจามิน ศาสตราจารย์สถิติเกษียณอายุแล้ว และผันตัวมาเป็นครูสอนสถิติโดยเฉพาะ ด้วยประสบการณ์และความเชี่ยวชาญที่กว้างขวางในสาขาสถิติ ฉันกระตือรือร้นที่จะแบ่งปันความรู้ของฉันเพื่อเสริมศักยภาพนักเรียนผ่าน Statorials. รู้เพิ่มเติม

t-test ของนักเรียนคืออะไร?

ประเภทของการทดสอบทีของนักเรียน

ตัวอย่างข้อสอบของนักเรียน

การทดสอบของนักเรียนสำหรับตัวอย่างอิสระ

การเบี่ยงเบนที่ไม่รู้จักและเท่ากัน

รูปแบบที่ไม่รู้จักและแตกต่างกัน

การทดสอบของนักเรียนสำหรับตัวอย่างที่จับคู่หรือเกี่ยวข้อง

สมมติฐานการทดสอบทีของนักเรียน

วิธีทำแบบทดสอบของนักเรียน

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

เพิ่มความคิดเห็น