การกระจายแบบล็อกนอร์มอล

โดย ดร.เบนจามิน แอนเดอร์สัน สิงหาคม 3, 2023 ความน่าจะเป็น 0 ความคิดเห็น

บทความนี้จะอธิบายว่าการแจกแจงแบบ Lognormal ในสถิติคืออะไร ดังนั้น คุณจะพบว่าคุณสมบัติของการแจกแจงแบบ Lognormal และกราฟของการแจกแจงความน่าจะเป็นประเภทนี้มีอะไรบ้าง

การแจกแจงแบบ Lognormal คืออะไร?

การแจกแจงแบบลอการิทึม หรือ การแจกแจงแบบลอการิทึม คือการแจกแจงความน่าจะเป็นที่กำหนดตัวแปรสุ่มซึ่งลอการิทึมเป็นไปตามการแจกแจงแบบปกติ

ดังนั้น หากตัวแปร X มีการแจกแจงแบบปกติ ฟังก์ชันเลขชี้กำลัง e ^x ก็จะมีการแจกแจงแบบล็อกนอร์มอล

$X\sim \text{Lognormal}(\mu,\sigma^2)$

โปรดทราบว่าการแจกแจงแบบลอการิทึมสามารถใช้ได้เฉพาะเมื่อค่าตัวแปรเป็นบวกเท่านั้น เนื่องจากลอการิทึมเป็นฟังก์ชันที่รับอาร์กิวเมนต์เชิงบวกเพียงตัวเดียวเท่านั้น

ในการใช้งานต่างๆ ของการแจกแจงแบบ Lognormal ในสถิติ เราจะแยกแยะการใช้การแจกแจงนี้เพื่อวิเคราะห์การลงทุนทางการเงินและดำเนินการวิเคราะห์ความน่าเชื่อถือ

การแจกแจงแบบลอจิกนอร์มัลเรียกอีกอย่าง ว่าการแจกแจง Tinaut ซึ่งบางครั้งก็เขียน เป็นการแจกแจงแบบลอจิกนอร์มัล หรือ การแจกแจงแบบลอจิกปกติ

โครงเรื่องของการกระจายแบบล็อกนอร์มอล

ตอนนี้เรารู้คำจำกัดความของการแจกแจงแบบลอจิคัลแล้ว เราจะมาดูในส่วนนี้ว่าการแสดงแบบกราฟิกของการแจกแจงแบบลอจิคัลจะแตกต่างกันไปอย่างไร ขึ้นอยู่กับค่าของค่าเฉลี่ยเลขคณิตและค่าเบี่ยงเบนมาตรฐาน

กราฟของฟังก์ชันความหนาแน่นของการแจกแจงแบบลอจิคัลเป็นดังนี้:

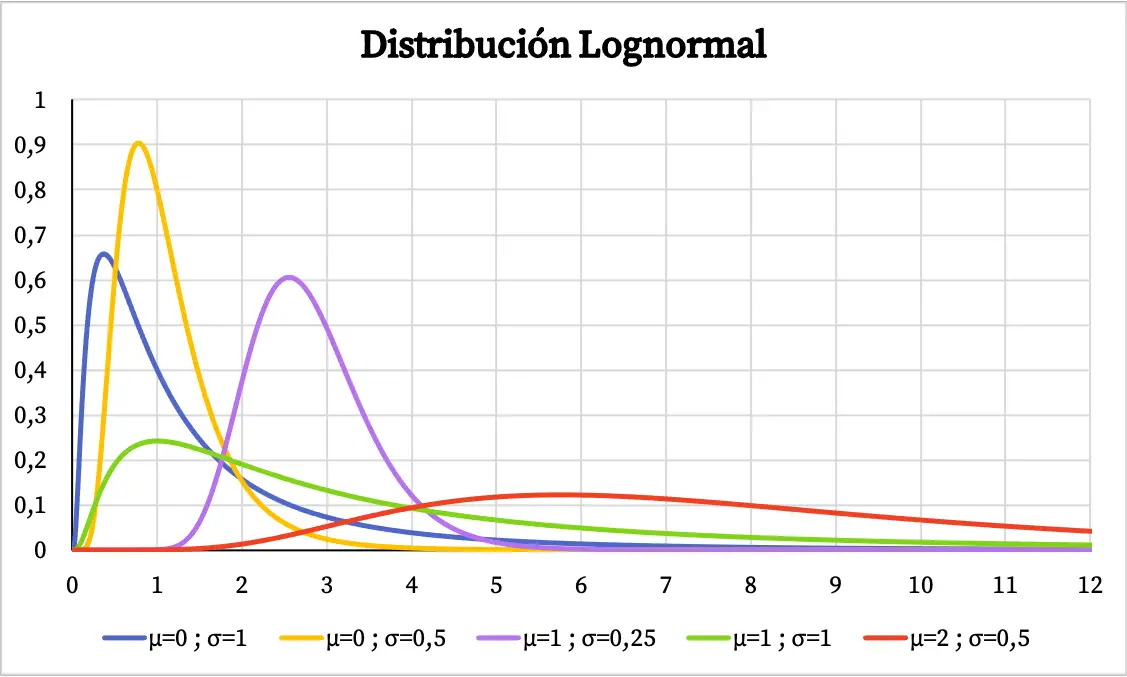
ในทางกลับกัน กราฟความน่าจะเป็นสะสมของการแจกแจงแบบลอจิคัลจะเป็นดังนี้:

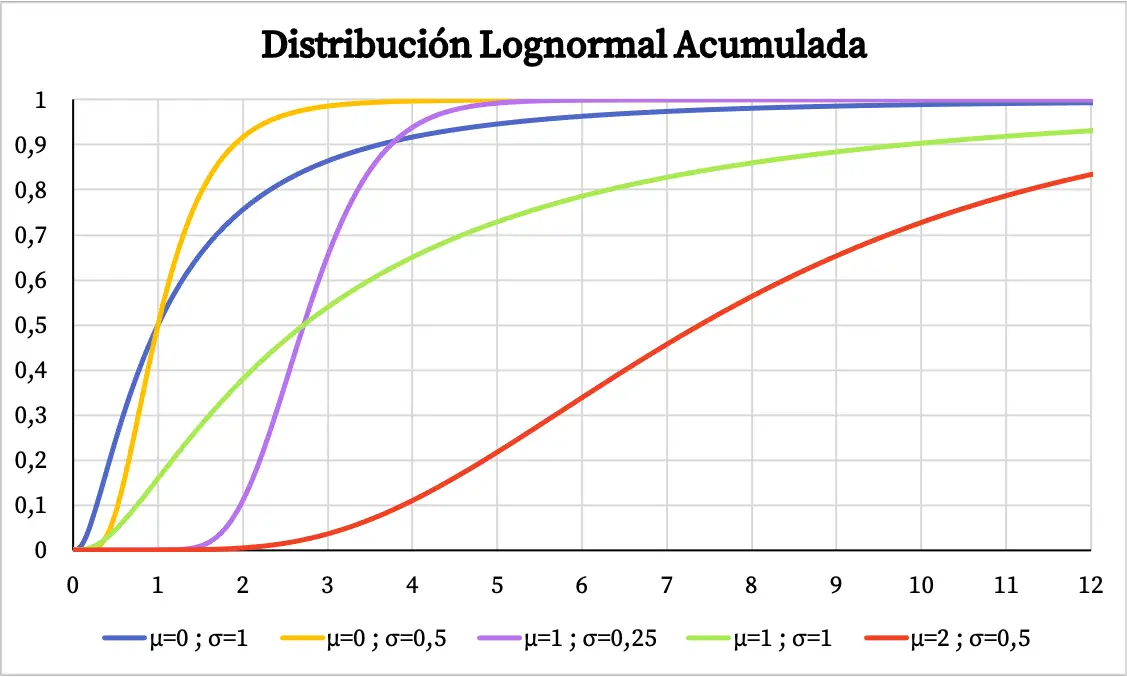
แผนภาพความน่าจะเป็นสะสมของการแจกแจงแบบลอจิกนอร์มอล

ลักษณะเฉพาะของการแจกแจงแบบล็อกนอร์มอล

การแจกแจงแบบ Lognormal มีลักษณะดังต่อไปนี้:

การแจกแจงแบบล็อกนอร์มอลถูกกำหนดโดยค่าของพารามิเตอร์สองตัว ค่าเฉลี่ยเลขคณิต μ และความแปรปรวน σ ²

$X\sim \text{Lognormal}(\mu,\sigma^2)$

โดเมนของการแจกแจงแบบลอจิคัลประกอบด้วยจำนวนจริงบวก เนื่องจากลอการิทึมไม่ยอมรับค่าลบหรือค่าศูนย์

$x\in (0,+\infty)$

ความคาดหมายของการแจกแจงแบบล็อกนอร์มัลจะเท่ากับจำนวน e ที่เพิ่มขึ้นเป็นผลรวมของค่าเฉลี่ยบวกกับความแปรปรวนหารด้วย 2

$\displaystyle E[X]=e^{\mu+\frac{\sigma^2}{2}}$

ในทางกลับกัน ความแปรปรวนของการแจกแจงแบบ Lognormal สามารถคำนวณได้ด้วยนิพจน์ต่อไปนี้:

$Var(X)=\left(e^{\sigma^2}-1\right)\cdot e^{2\mu+\sigma^2$

โหมดของการแจกแจงแบบล็อกนอร์มัลนั้นเทียบเท่ากับจำนวน e ที่เพิ่มขึ้นตามค่าเฉลี่ยของการแจกแจง

$Mo=e^\mu$

ค่าสัมประสิทธิ์ความเบ้ของการแจกแจงแบบลอจิคัลสามารถกำหนดได้โดยใช้สูตรต่อไปนี้:

$\displaystyle A=\left(e^{\sigma^2}+2\right)\cdot\sqrt{e^{\sigma^2}-1}$

สูตรสำหรับฟังก์ชันความหนาแน่นของการแจกแจงแบบลอจิคัลคือ:

$\displaystyle P[X=x]=\frac{1}{\sigma \cdot x\cdot \sqrt{2 \pi}}\cdot \exp\left(-\frac{(\ln x-\mu)^2}{2\sigma^2}\right)$

สูตรสำหรับฟังก์ชันความน่าจะเป็นสะสมของการแจกแจงแบบลอจิคัลคือ:

$\displaystyle P[X\leq x]=\Phi\left(\frac{\ln x-\mu}{\sigma}\right)$

ทอง

$\Phi$

คือฟังก์ชันความน่าจะเป็นสะสมของ การแจกแจงแบบปกติมาตรฐาน

ค่าเฉลี่ยเลขคณิตของการแจกแจงแบบล็อกนอร์มัลมีค่ามากกว่าค่ามัธยฐาน

$\mu > Me” title=”Rendered by QuickLaTeX.com” height=”16″ width=”61″ style=”vertical-align: -4px;”></p></p> </div>  <div class=$

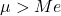
เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

สวัสดี ฉันชื่อเบนจามิน ศาสตราจารย์สถิติเกษียณอายุแล้ว และผันตัวมาเป็นครูสอนสถิติโดยเฉพาะ ด้วยประสบการณ์และความเชี่ยวชาญที่กว้างขวางในสาขาสถิติ ฉันกระตือรือร้นที่จะแบ่งปันความรู้ของฉันเพื่อเสริมศักยภาพนักเรียนผ่าน Statorials. รู้เพิ่มเติม

การแจกแจงแบบ Lognormal คืออะไร?

โครงเรื่องของการกระจายแบบล็อกนอร์มอล

ลักษณะเฉพาะของการแจกแจงแบบล็อกนอร์มอล

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

เพิ่มความคิดเห็น