Somers' d คืออะไร? (คำจำกัดความ & #038; ตัวอย่าง)
Somers’ D ย่อมาจาก Somers’ Delta เป็นตัววัดความแรงและทิศทางของความสัมพันธ์ระหว่างตัวแปรตามลำดับและตัวแปรอิสระลำดับ
ตัวแปร ลำดับ คือตัวแปรที่ค่ามีลำดับตามธรรมชาติ (เช่น “ไม่ดี” “เป็นกลาง” “ดี”)
ค่าของ Somers’ D อยู่ระหว่าง -1 ถึง 1 โดยที่:
- -1: บ่งชี้ว่าคู่ของตัวแปรทั้งหมดไม่สอดคล้องกัน
- 1: บ่งชี้ว่าคู่ตัวแปรทั้งหมดตรงกัน
Somers’ D ถูกนำมาใช้ในทางปฏิบัติสำหรับวิธีการทางสถิติแบบไม่อิงพารามิเตอร์หลายวิธี
ซอมเมอร์ส ดี: คำจำกัดความ
เมื่อพิจารณาตัวแปรสองตัวคือ X และ Y เราสามารถพูดได้ว่า:
- สองคู่ (x i , y i ) และ (x j , y j ) มี ความสอดคล้องกัน หากอันดับของทั้งสององค์ประกอบตรงกัน
- สองคู่ (x i , y i ) และ (x j , y j ) ไม่ลงรอยกัน หากอันดับของทั้งสององค์ประกอบตรงกัน
จากนั้นเราสามารถคำนวณ Somers’ D ได้โดยใช้สูตรต่อไปนี้:
ซอมเมอร์ D = ( NC – N D ) / ( NC + N D + N T )
ทอง:
- NC : จำนวนคู่ที่ตรงกัน
- ND : จำนวนคู่ที่ไม่ลงรอยกัน
- N T : จำนวนคู่ที่เสมอกัน
ค่าผลลัพธ์จะอยู่ระหว่าง -1 ถึง 1 เสมอ
Somers’ D: ตัวอย่างใน R
สมมติว่าร้านขายของชำต้องการประเมินความสัมพันธ์ระหว่างตัวแปรลำดับสองตัวต่อไปนี้:
- ความเป็นมิตรโดยรวมของแคชเชียร์ (อันดับ 1 ถึง 3)
- ความพึงพอใจต่อประสบการณ์โดยรวมของลูกค้า (อันดับ 1 ถึง 3 เช่นกัน)
พวกเขารวบรวมคะแนนต่อไปนี้จาก กลุ่มตัวอย่าง ลูกค้า 10 ราย:
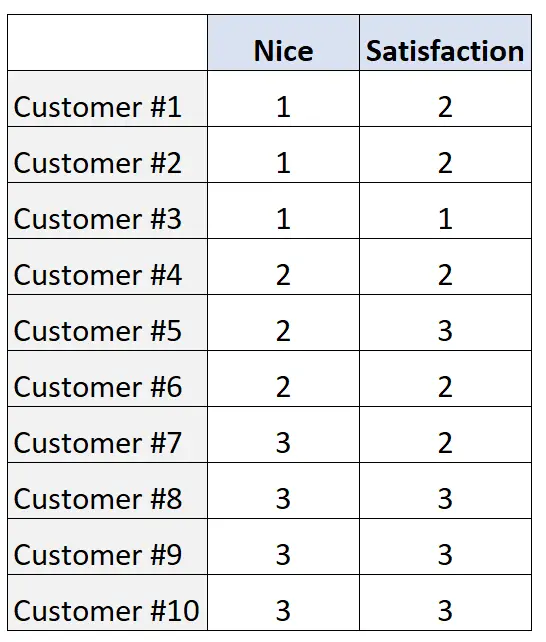
ในการหาปริมาณความสัมพันธ์ระหว่างตัวแปรทั้งสอง เราสามารถคำนวณ Somers’ D ได้โดยใช้โค้ดต่อไปนี้ใน R:
#enter data nice <- c(1, 1, 1, 2, 2, 2, 3, 3, 3, 3) satisfaction <- c(2, 2, 1, 2, 3, 2, 2, 3, 3, 3) #load DescTools package library(DescTools) #calculate Somers' D SomersDelta(nice, satisfaction) [1] 0.6896552
Somers’ D กลายเป็น 0.6896552
ค่านี้ค่อนข้างใกล้กับ 1 ซึ่งบ่งชี้ว่ามีความสัมพันธ์เชิงบวกที่ค่อนข้างชัดเจนระหว่างตัวแปรทั้งสอง
สิ่งนี้สมเหตุสมผล: ลูกค้าที่ให้คะแนนพนักงานเก็บเงินว่าดีกว่ามักจะให้คะแนนความพึงพอใจโดยรวมสูงกว่าด้วย
แหล่งข้อมูลเพิ่มเติม
ความรู้เบื้องต้นเกี่ยวกับสัมประสิทธิ์สหสัมพันธ์เพียร์สัน
ความรู้เบื้องต้นเกี่ยวกับ Tau ของ Kendall