วิธีการ bootstrapping ใน r (พร้อมตัวอย่าง)

การบูตสแตรปปิ้ง เป็นวิธีการที่สามารถใช้เพื่อประมาณค่าความคลาดเคลื่อนมาตรฐานของ สถิติ ใดๆ และสร้าง ช่วงความเชื่อมั่น สำหรับสถิตินั้น

กระบวนการพื้นฐานสำหรับการบูตสแตรปมีดังนี้:

• นำตัวอย่าง k ซ้ำโดยแทนที่จากชุดข้อมูลที่กำหนด
• สำหรับแต่ละตัวอย่าง ให้คำนวณสถิติที่น่าสนใจ
• ค่านี้ให้ค่าประมาณที่แตกต่างกัน k สำหรับสถิติหนึ่งๆ ซึ่งคุณสามารถใช้คำนวณค่าความผิดพลาดมาตรฐานของสถิติและสร้างช่วงความเชื่อมั่นสำหรับสถิตินั้นได้

เราสามารถบูตสแตรปใน R โดยใช้ฟังก์ชันต่อไปนี้จาก ไลบรารีบูตสแตรป :

1. สร้างตัวอย่างบูตสแตรป

บูต (ข้อมูล, สถิติ, R, …)

ทอง:

• ข้อมูล: เวกเตอร์ เมทริกซ์ หรือบล็อกของข้อมูล
• สถิติ: ฟังก์ชันที่สร้างสถิติที่จะเริ่มต้น
• ตอบ: จำนวนการบูตสแตรปซ้ำ

2. สร้างช่วงความเชื่อมั่นบูตสแตรป

boot.ci (วัตถุสำหรับบูต, conf, พิมพ์)

ทอง:

• bootobject: วัตถุที่ส่งคืนโดยฟังก์ชัน boot()
• conf: ช่วงความเชื่อมั่นที่จะคำนวณ ค่าเริ่มต้นคือ 0.95
• type: ประเภทของช่วงความเชื่อมั่นที่จะคำนวณ ตัวเลือกประกอบด้วย ‘มาตรฐาน’ ‘พื้นฐาน’ ‘สตั๊ด’ ‘perc’ ‘bca’ และ ‘ทั้งหมด’ – ค่าเริ่มต้นคือ ‘ทั้งหมด’

ตัวอย่างต่อไปนี้แสดงวิธีใช้ฟังก์ชันเหล่านี้ในทางปฏิบัติ

ตัวอย่างที่ 1: บูตสแตรปสถิติเดียว

รหัสต่อไปนี้แสดงวิธีการคำนวณข้อผิดพลาดมาตรฐานสำหรับ R-squared ของแบบจำลองการถดถอยเชิงเส้นอย่างง่าย:

 set.seed(0)
library (boot)

#define function to calculate R-squared
rsq_function <- function (formula, data, indices) {
  d <- data[indices,] #allows boot to select sample
  fit <- lm(formula, data=d) #fit regression model
  return (summary(fit)$r.square) #return R-squared of model
}
#perform bootstrapping with 2000 replications
reps <- boot(data=mtcars, statistic=rsq_function, R=2000, formula=mpg~disp)

#view results of boostrapping
reps

ORDINARY NONPARAMETRIC BOOTSTRAP


Call:
boot(data = mtcars, statistic = rsq_function, R = 2000, formula = mpg ~ 
    available)


Bootstrap Statistics:
     original bias std. error
t1* 0.7183433 0.002164339 0.06513426

จากผลลัพธ์เราจะเห็นได้ว่า:

• ค่า R-squared โดยประมาณสำหรับแบบจำลองการถดถอยนี้คือ 0.7183433
• ข้อผิดพลาดมาตรฐานสำหรับการประมาณนี้คือ 0.06513426

นอกจากนี้เรายังสามารถแสดงภาพการกระจายตัวอย่างที่บูตสแตรปได้อย่างรวดเร็ว:

 plot(reps)

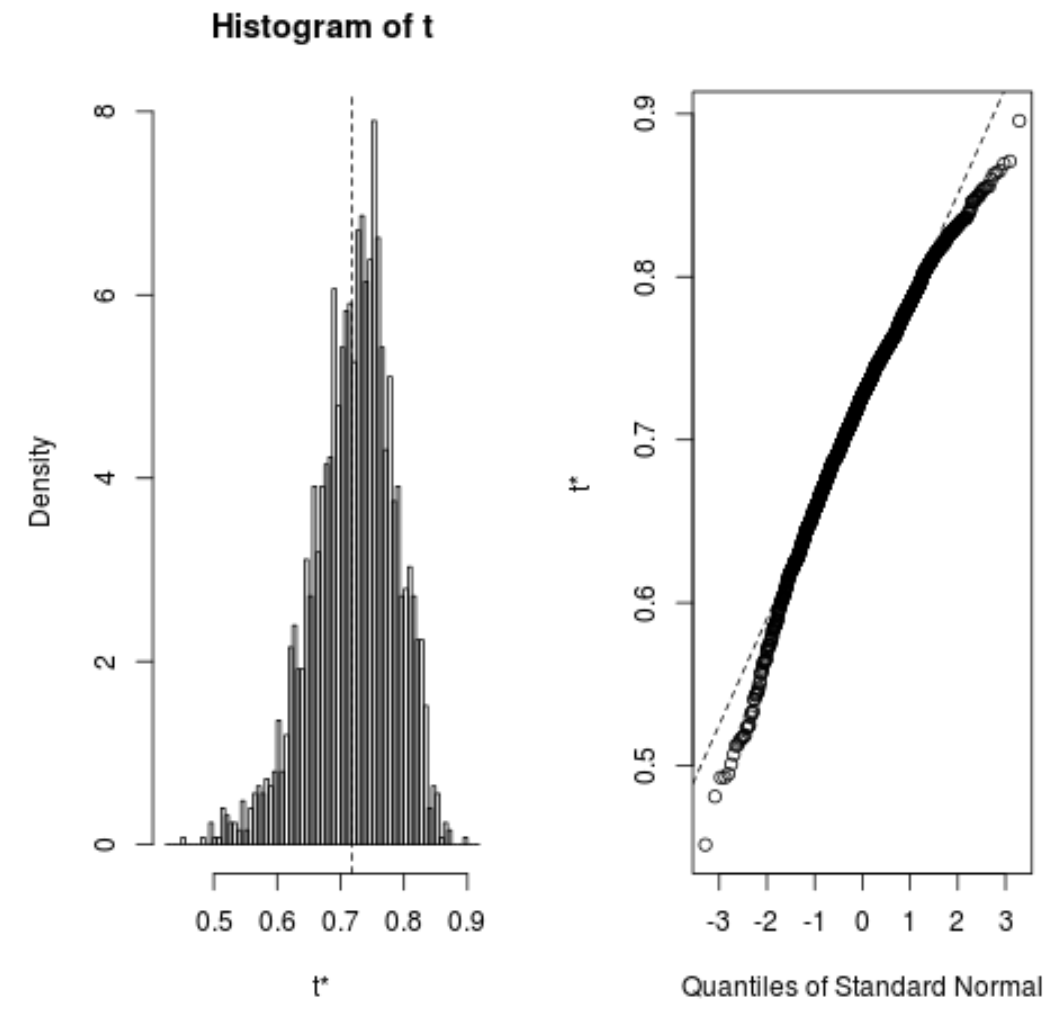
นอกจากนี้เรายังสามารถใช้โค้ดต่อไปนี้เพื่อคำนวณช่วงความเชื่อมั่น 95% สำหรับค่า R-squared โดยประมาณของโมเดล:

 #calculate adjusted bootstrap percentile (BCa) interval
boot.ci(reps, type=" bca ")

CALL: 
boot.ci(boot.out = reps, type = "bca")

Intervals: 
Level BCa          
95% (0.5350, 0.8188)  
Calculations and Intervals on Original Scale

จากผลลัพธ์ เราจะเห็นว่าช่วงความเชื่อมั่น 95% ที่บูตสแตรปสำหรับค่า R-squared ที่แท้จริงคือ (0.5350, 0.8188)

ตัวอย่างที่ 2: บูตสแตรปสถิติหลายรายการ

รหัสต่อไปนี้แสดงวิธีการคำนวณข้อผิดพลาดมาตรฐานสำหรับแต่ละสัมประสิทธิ์ในแบบจำลองการถดถอยเชิงเส้นหลายตัว:

 set.seed(0)
library (boot)

#define function to calculate fitted regression coefficients
coef_function <- function (formula, data, indices) {
  d <- data[indices,] #allows boot to select sample
  fit <- lm(formula, data=d) #fit regression model
  return (coef(fit)) #return coefficient estimates of model
}

#perform bootstrapping with 2000 replications
reps <- boot(data=mtcars, statistic=coef_function, R=2000, formula=mpg~disp)

#view results of boostrapping
reps

ORDINARY NONPARAMETRIC BOOTSTRAP


Call:
boot(data = mtcars, statistic = coef_function, R = 2000, formula = mpg ~ 
    available)


Bootstrap Statistics:
       original bias std. error
t1* 29.59985476 -5.058601e-02 1.49354577
t2* -0.04121512 6.549384e-05 0.00527082

จากผลลัพธ์เราจะเห็นได้ว่า:

• ค่าสัมประสิทธิ์โดยประมาณสำหรับการสกัดกั้นโมเดลคือ 29.59985476 และข้อผิดพลาดมาตรฐานของการประมาณนี้คือ 1.49354577
• ค่าสัมประสิทธิ์โดยประมาณสำหรับการ กระจาย ตัวแปรทำนายในแบบจำลองคือ -0.04121512 และข้อผิดพลาดมาตรฐานของการประมาณนี้คือ 0.00527082

นอกจากนี้เรายังสามารถแสดงภาพการกระจายตัวอย่างที่บูตสแตรปได้อย่างรวดเร็ว:

 plot(reps, index=1) #intercept of model
plot(reps, index=2) #disp predictor variable

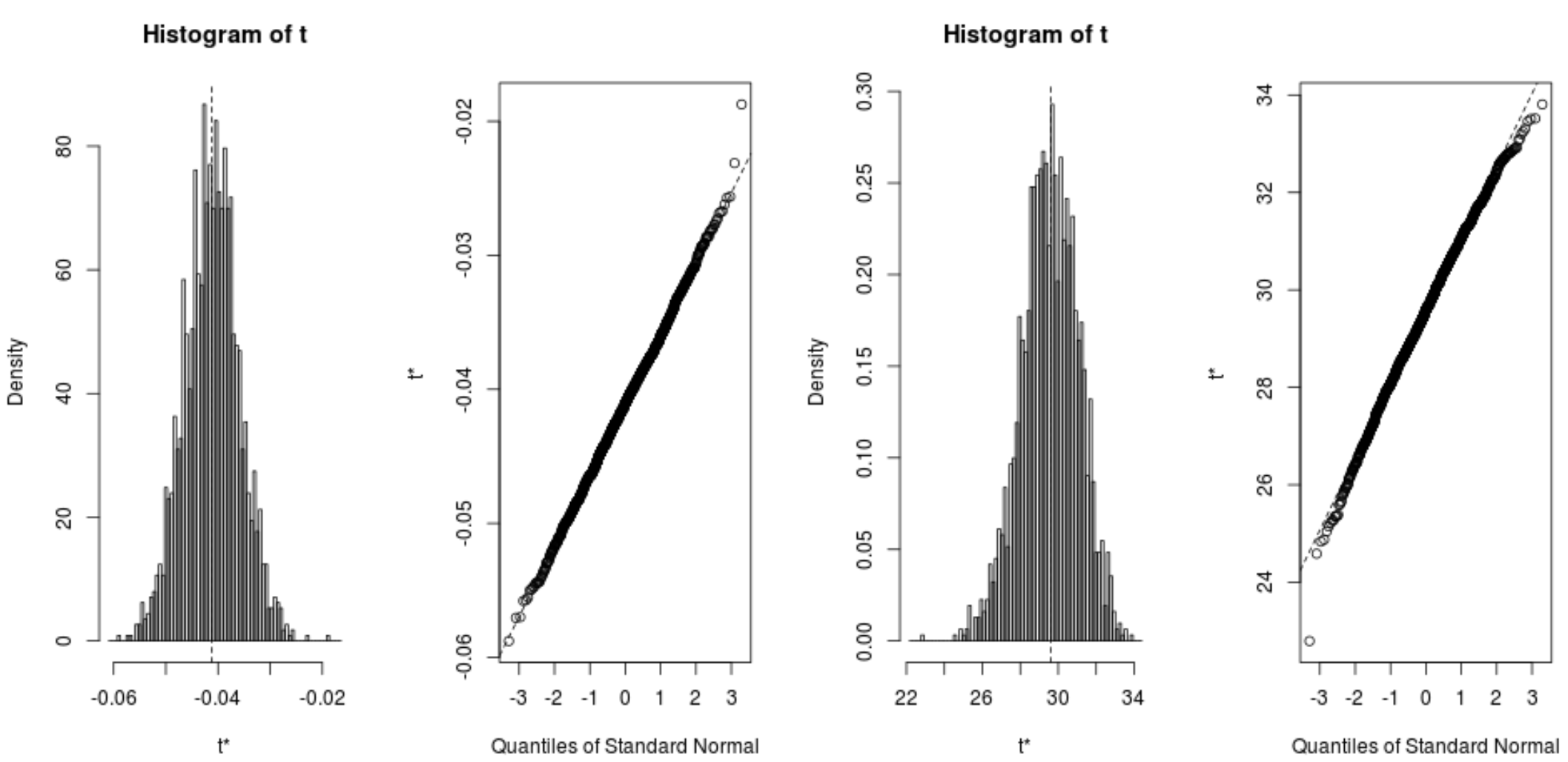
นอกจากนี้เรายังสามารถใช้โค้ดต่อไปนี้เพื่อคำนวณช่วงความเชื่อมั่น 95% สำหรับแต่ละสัมประสิทธิ์:

 #calculate adjusted bootstrap percentile (BCa) intervals
boot.ci(reps, type=" bca ", index=1) #intercept of model
boot.ci(reps, type=" bca ", index=2) #disp predictor variable

CALL: 
boot.ci(boot.out = reps, type = "bca", index = 1)

Intervals: 
Level BCa          
95% (26.78, 32.66)  
Calculations and Intervals on Original Scale
BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
Based on 2000 bootstrap replicates

CALL: 
boot.ci(boot.out = reps, type = "bca", index = 2)

Intervals: 
Level BCa          
95% (-0.0520, -0.0312)  
Calculations and Intervals on Original Scale

จากผลลัพธ์ เราจะเห็นว่าช่วงความเชื่อมั่น 95% ที่บูตสแตรปสำหรับสัมประสิทธิ์แบบจำลองมีดังนี้:

• ไอซีสำหรับการสกัดกั้น: (26.78, 32.66)
• CI สำหรับ จอแสดงผล : (-.0520, -.0312)

แหล่งข้อมูลเพิ่มเติม

วิธีดำเนินการถดถอยเชิงเส้นอย่างง่ายใน R
วิธีดำเนินการถดถอยเชิงเส้นพหุคูณใน R
ข้อมูลเบื้องต้นเกี่ยวกับช่วงความเชื่อมั่น