พล็อตกล่องและมัสสุ

โดย ดร.เบนจามิน แอนเดอร์สัน สิงหาคม 5, 2023 สถิติ 0 ความคิดเห็น

บทความนี้จะอธิบายว่า Boxplot หรือที่เรียกว่า Box Plot (หรือ Boxplot) คืออะไร คุณจะค้นพบว่าไดอะแกรมทางสถิติประเภทนี้ถูกสร้างขึ้นมาอย่างไร และแบบฝึกหัดแก้ไขไดอะแกรมกล่องและมัสสุและการตีความของมัน

พล็อตกล่องและมัสสุคืออะไร?

Boxplot หรือที่เรียกว่า Boxplot หรือ Boxplot คือกราฟที่แสดงชุดข้อมูลทางสถิติโดยใช้ควอไทล์

ลักษณะหลักของพล็อตกล่องและมัสสุคือช่วยให้คุณเห็นภาพการกระจายตัวของชุดข้อมูลได้อย่างรวดเร็ว เนื่องจากมันระบุควอไทล์ ค่ามัธยฐาน ค่าสุดขีด และค่าผิดปกติของข้อมูล

ดังนั้นไดอะแกรมประเภทนี้จึงประกอบด้วยกล่องสี่เหลี่ยมและสองสามบรรทัด (หรือหนวด) ซึ่งมีค่าต่อไปนี้ปรากฏ:

ขอบเขตของกล่องระบุ ควอร์ไทล์ที่หนึ่งและสาม (Q ₁ และ Q ₃ ) และเส้นแนวตั้งภายในกล่องคือ ค่ามัธยฐาน (เทียบเท่ากับควอไทล์ที่สอง _Q2 )
ขีดจำกัดของหนวด (หรือแขน) คือ ค่าสุดขั้ว ซึ่งก็คือค่าต่ำสุดและค่าสูงสุดของชุดข้อมูล
จุดที่อยู่นอกหนวดคือ ค่าผิดปกติ หรืออีกนัยหนึ่งคือข้อมูลที่อาจมีการวัดอย่างไม่ถูกต้อง และ ดังนั้นจึงไม่ควรนำมาพิจารณาในการศึกษาทางสถิติ

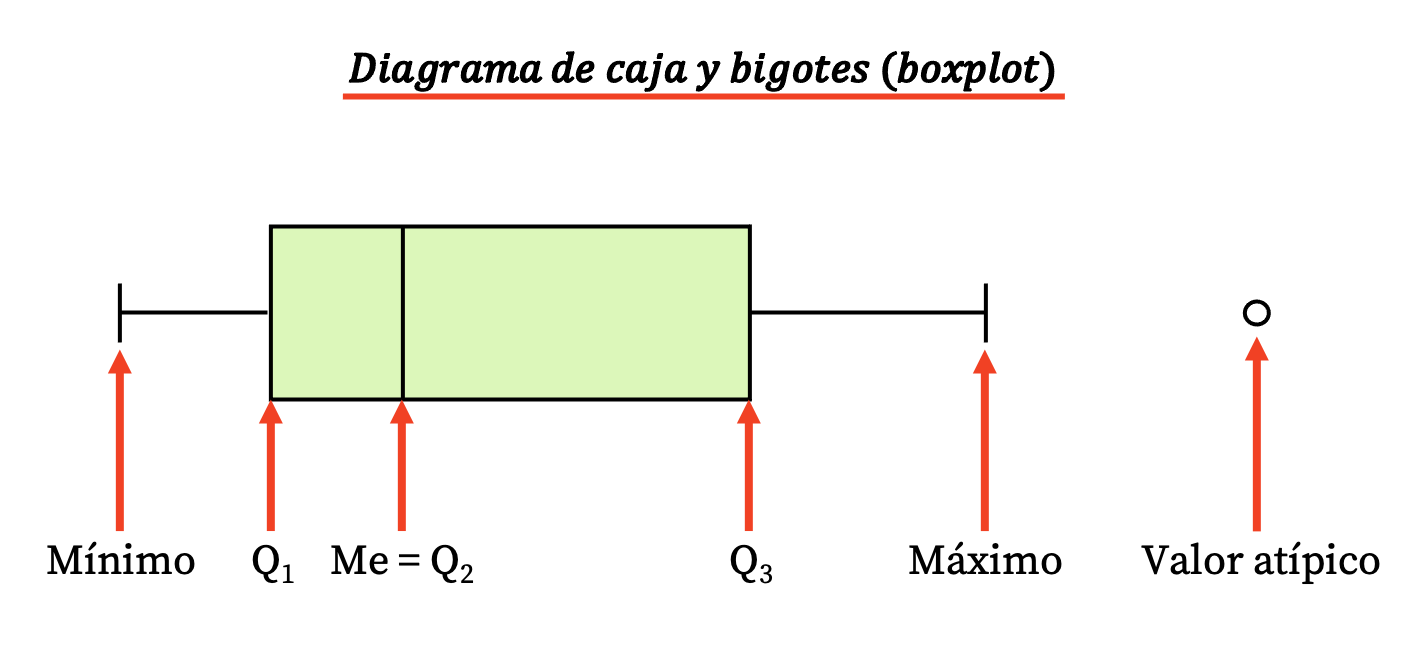
โปรดทราบว่าความแตกต่างระหว่างควอไทล์ที่สามและควอไทล์ที่ 1 คือช่วงระหว่างควอไทล์ (หรือช่วงระหว่างควอไทล์) ซึ่งเป็นการวัดการกระจายตัวทางสถิติอีกรูปแบบหนึ่ง

แปลงกล่องและมัสสุมีประโยชน์มากสำหรับการเปรียบเทียบตัวแปรตัวเลข อย่างไรก็ตาม ไม่เหมาะที่จะใช้แทนตัวแปรประเภท

วิธีการสร้างพล็อตกล่องและมัสสุ

หากต้องการสร้างพล็อตกล่องและมัสสุ (หรือ boxplot) จากชุดข้อมูล ต้องดำเนินการขั้นตอนต่อไปนี้:

จัดเรียงตัวอย่างข้อมูลทางสถิติ
คำนวณควอร์ไทล์ (Q ₁ , Q ₂ และ Q ₃ ) และแสดงเป็นกล่องในแผนภาพ ควอร์ไทล์ที่หนึ่งและสามสอดคล้องกับขีดจำกัดของกล่อง และเพื่อที่จะเป็นตัวแทนของค่ามัธยฐาน (ควอไทล์ที่สอง) คุณต้องลากเส้นภายในกล่องซึ่งมีค่าอยู่
คำนวณช่วงระหว่างควอร์ไทล์ ซึ่งเท่ากับควอไทล์ที่ 3 ลบด้วยควอร์ไทล์ที่ 1

$IQR=Q_3-Q_1$

คำนวณค่าที่ยอมรับได้ LI และ LS โดยมีสูตรดังนี้:

$LI=Q_1-1,5\cdot IQR$

$LS=Q_3+1,5\cdot IQR$

ระบุค่าผิดปกติของตัวอย่างซึ่งเป็นค่าน้อยกว่า LI หรือมากกว่า LS นำเสนอค่าเหล่านี้นอกช่วงมัสสุด้วยจุด
ระบุและแสดงค่าสุดขั้วซึ่งเป็นค่าที่น้อยที่สุดและค่าที่ใหญ่ที่สุดในช่วงเวลาที่เกิดจาก LI และ LS ค่าเหล่านี้แสดงถึงจุดสิ้นสุดของหนวดทั้งสองในแผนภาพ

ตัวอย่างโครงเรื่องกล่องและมัสสุ

เมื่อพิจารณาถึงคำจำกัดความและทฤษฎีของพล็อตกล่องและมัสสุ (หรือบ็อกซ์พล็อต) คุณจะพบตัวอย่างที่เป็นรูปธรรมด้านล่างเพื่อทำความเข้าใจแนวคิดได้ดีขึ้น และดูว่าพล็อตทางสถิติประเภทนี้ดำเนินการอย่างไร

วาด Boxplot ของชุดข้อมูลทางสถิติต่อไปนี้

ในกรณีนี้ ข้อมูลจะเรียงลำดับจากน้อยไปหามากอยู่แล้ว ดังนั้นจึงไม่จำเป็นต้องเปลี่ยนแปลง มิฉะนั้นเราควรเรียงลำดับข้อมูลตัวอย่างก่อน

ประการที่สอง เราแยกควอไทล์ของกลุ่มตัวอย่าง:

$Q_1=4,06$

$Q_2=4,38$

$Q_3=4,66$

➤ ดู: เครื่องคิดเลขควอไทล์

เมื่อเราคำนวณควอร์ไทล์ทั้งสามแล้ว เราจะหาพิสัยระหว่างควอไทล์ด้วยการลบควอไทล์ 3 ลบควอไทล์ 1:

$IQR=Q_3-Q_1=4,66-4,06=0,6$

ตอนนี้เราคำนวณขีดจำกัด LI และ LS ซึ่งเป็นค่าที่ถือว่าข้อมูลไม่ปกติ เมื่อต้องการทำเช่นนี้ คุณต้องใช้สูตรต่อไปนี้:

$LI=Q_1-1,5\cdot IQR=4,06-1,5\cdot 0,6=3,16$

$LS=Q_3+1,5\cdot IQR=4,66+1,5\cdot 0,6=5,56$

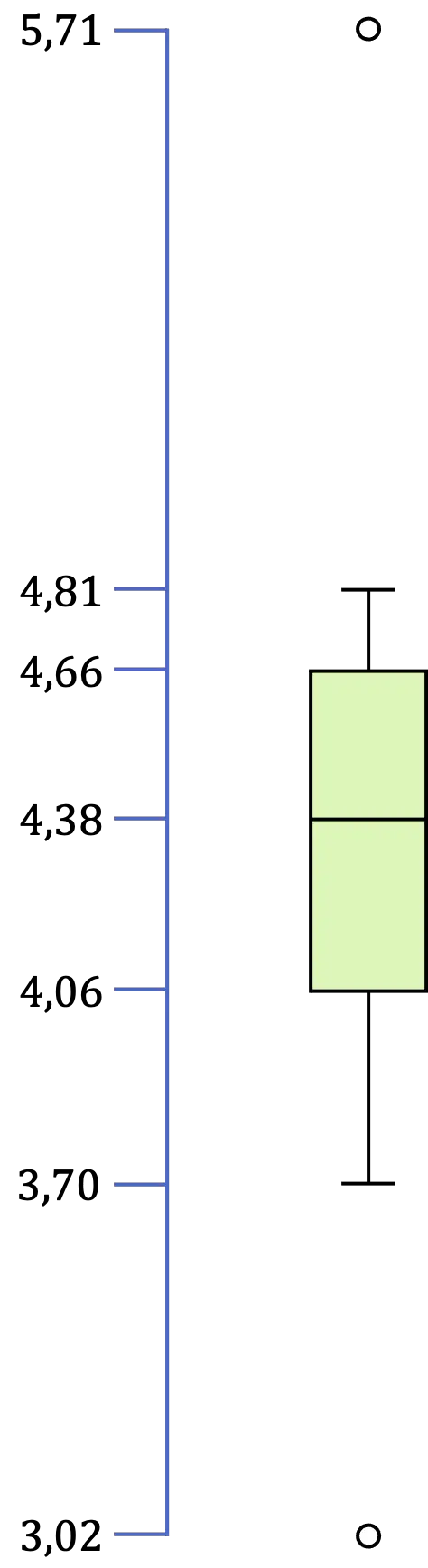
ในกรณีนี้ เรามีค่าผิดปกติสองตัว เนื่องจาก 3.02 น้อยกว่า 3.16 และ 5.71 มากกว่า 5.56

$\text{Valores at\'ipicos} =\Bigl\{3,02 \ ; \ 5,71\Bigr\}$

สุดท้ายนี้ ยังคงต้องระบุค่าสุดขั้วซึ่งเป็นค่าต่ำสุดและสูงสุดของข้อมูลทั้งหมดที่อยู่ในช่วงเวลา [LI,LS] ดังนั้น ในตัวอย่างของเรา ค่าต่ำสุดคือ 3.70 และค่าสูงสุดคือ 4.81

$\text{M\'inimo}=3,70$

$\text{M\'aximo}=4,81$

ดังนั้นเมื่อเราระบุค่าทั้งหมดของกล่องและแผนภาพมัสสุแล้ว สิ่งที่เหลืออยู่คือการแสดงภาพกราฟิก:

พล็อตกล่องและมัสสุมีไว้ทำอะไร?

สุดท้ายเรามาดูกันว่ามีไว้เพื่ออะไรและจะตีความพล็อตกล่องและมัสสุ (หรือ boxplot) อย่างไร

เห็นได้ชัดว่าพล็อตกล่องและมัสสุมีประโยชน์มากสำหรับการรู้ควอไทล์ ช่วงระหว่างควอไทล์ ค่ามัธยฐาน ค่าสุดขีด และค่าผิดปกติของชุดข้อมูลอย่างรวดเร็ว เนื่องจากการวัดทางสถิติทั้งหมดนี้สามารถระบุได้ด้วยการดูง่ายๆ

นอกจากนี้ แผนภาพกล่องและหนวดเครายังใช้ในการวิเคราะห์ความสมมาตรของตัวอย่างทางสถิติ เนื่องจากแสดงให้เห็นชุดข้อมูลทั้งหมดด้วยสายตา หากค่ามัธยฐานไม่อยู่ตรงกลางกล่อง แสดงว่าตัวอย่างไม่สมมาตร

ในทำนองเดียวกัน Boxplots ถูกนำมาใช้กันอย่างแพร่หลายในตลาดหุ้นเพื่อแสดงการเปลี่ยนแปลงของราคาหุ้นในช่วงเวลาหนึ่ง เนื่องจากทำให้มองเห็นมูลค่าสูงสุด ค่าต่ำสุด และค่ากลางในช่วงเวลาสั้นๆ เวลาจึงทำให้ตัดสินใจได้เร็วขึ้น

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

สวัสดี ฉันชื่อเบนจามิน ศาสตราจารย์สถิติเกษียณอายุแล้ว และผันตัวมาเป็นครูสอนสถิติโดยเฉพาะ ด้วยประสบการณ์และความเชี่ยวชาญที่กว้างขวางในสาขาสถิติ ฉันกระตือรือร้นที่จะแบ่งปันความรู้ของฉันเพื่อเสริมศักยภาพนักเรียนผ่าน Statorials. รู้เพิ่มเติม