วิธีการพล็อตเส้นโค้งการถดถอยพหุนามใน r

การถดถอยพหุนาม เป็นเทคนิคการถดถอยที่เราใช้เมื่อความสัมพันธ์ระหว่างตัวแปรทำนายและ ตัวแปรตอบสนอง ไม่เป็นเชิงเส้น

บทช่วยสอนนี้จะอธิบายวิธีการพล็อตเส้นโค้งการถดถอยพหุนามใน R

ที่เกี่ยวข้อง: 7 ประเภทของการถดถอยที่พบบ่อยที่สุด

ตัวอย่าง: การวางแผนเส้นโค้งการถดถอยพหุนามใน R

โค้ดต่อไปนี้แสดงวิธีปรับโมเดลการถดถอยพหุนามให้พอดีกับชุดข้อมูล จากนั้นจึงลงจุดเส้นโค้งการถดถอยพหุนามบนข้อมูลดิบใน Scatterplot:

 #define data
x <- runif(50, 5, 15)
y <- 0.1*x^3 - 0.5 * x^2 - x + 5 + rnorm(length(x),0,10) 
 
#plot x vs. y
plot(x, y, pch= 16 , cex= 1.5 ) 
 
#fit polynomial regression model
fit <- lm(y ~ x + I(x^2) + I(x^3))
 
#use model to get predicted values
pred <- predict(fit)
ix <- sort(x, index. return = T )$ix

#add polynomial curve to plot
lines(x[ix], pred[ix], col=' red ', lwd= 2 )

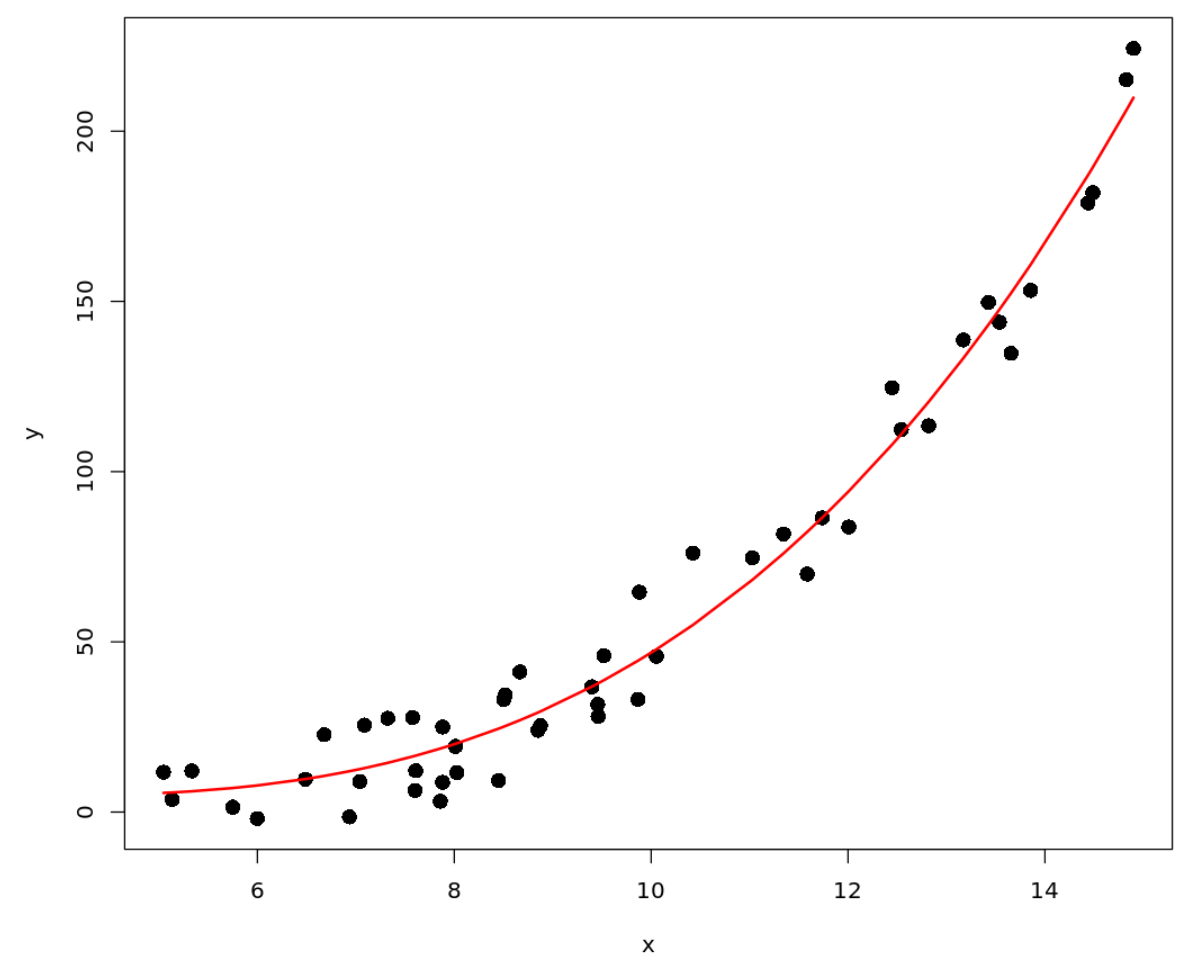
นอกจากนี้เรายังสามารถเพิ่มสมการการถดถอยพหุนามแบบพอดีลงในพล็อตโดยใช้ฟังก์ชัน text() :

 #define data
x <- runif(50, 5, 15)
y <- 0.1*x^3 - 0.5 * x^2 - x + 5 + rnorm(length(x),0,10) 
 
#plot x vs. y
plot(x, y, pch=16, cex=1.5) 
 
#fit polynomial regression model
fit <- lm(y ~ x + I(x^2) + I(x^3))
 
#use model to get predicted values
pred <- predict(fit)
ix <- sort(x, index. return = T )$ix

#add polynomial curve to plot
lines(x[ix], pred[ix], col=' red ', lwd= 2 )

#get model coefficients
coeff <- round(fit$coefficients, 2)

#add fitted model equation to plot
text(9, 200 , paste("Model: ", coeff[1], " + ", coeff[2],
                    "*x", "+", coeff[3], "*x^2", "+", coeff[4], "*x^3"), cex= 1.3 )

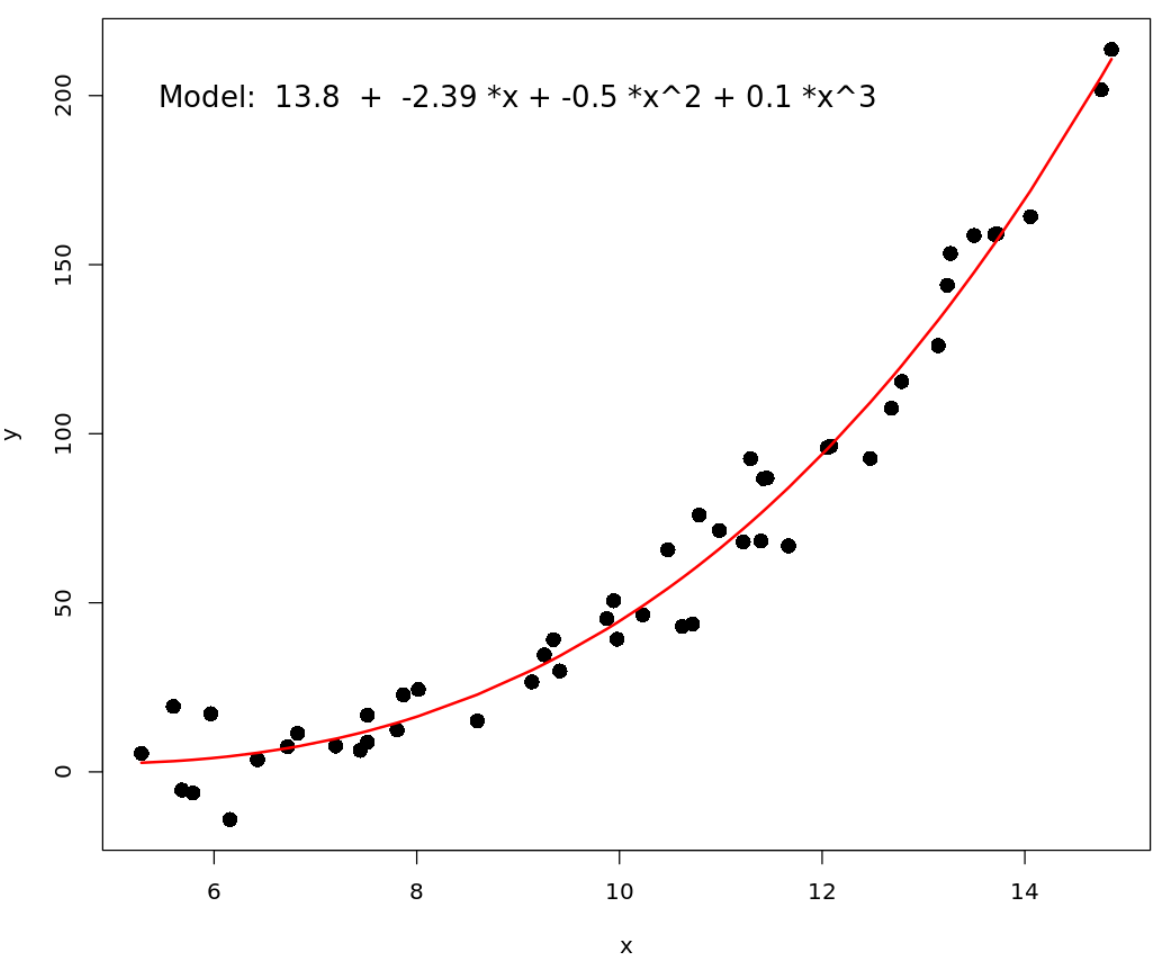
โปรดทราบว่าอาร์กิวเมนต์ cex ควบคุมขนาดตัวอักษรของข้อความ ค่าเริ่มต้นคือ 1 ดังนั้นเราจึงเลือกใช้ค่า 1.3 เพื่อทำให้ข้อความอ่านง่ายขึ้น

แหล่งข้อมูลเพิ่มเติม

ความรู้เบื้องต้นเกี่ยวกับการถดถอยพหุนาม
วิธีปรับเส้นโค้งพหุนามใน Excel ให้พอดี
วิธีดำเนินการถดถอยพหุนามใน Python