วิธีใช้ฟังก์ชัน lm() ใน r เพื่อให้พอดีกับโมเดลเชิงเส้น

ฟังก์ชัน lm() ใน R ใช้เพื่อปรับโมเดลการถดถอยเชิงเส้นให้เหมาะสม

ฟังก์ชันนี้ใช้ไวยากรณ์พื้นฐานต่อไปนี้:

lm(สูตร ข้อมูล …)

ทอง:

• สูตร: สูตรโมเดลเชิงเส้น (เช่น y ~ x1 + x2)
• data: ชื่อของบล็อกข้อมูลที่มีข้อมูล

ตัวอย่างต่อไปนี้แสดงวิธีการใช้ฟังก์ชันนี้ใน R เพื่อทำสิ่งต่อไปนี้:

• ติดตั้งโมเดลการถดถอย
• ดูสรุปความพอดีของโมเดลการถดถอย
• ดูแผนการวินิจฉัยโมเดล
• พล็อตโมเดลการถดถอยที่ติดตั้งไว้
• คาดการณ์โดยใช้แบบจำลองการถดถอย

พอดีกับแบบจำลองการถดถอย

รหัสต่อไปนี้แสดงวิธีใช้ฟังก์ชัน lm() เพื่อให้พอดีกับโมเดลการถดถอยเชิงเส้นใน R:

 #define data
df = data. frame (x=c(1, 3, 3, 4, 5, 5, 6, 8, 9, 12),
                y=c(12, 14, 14, 13, 17, 19, 22, 26, 24, 22))

#fit linear regression model using 'x' as predictor and 'y' as response variable
model <- lm(y ~ x, data=df)

แสดงสรุปโมเดลการถดถอย

จากนั้นเราสามารถใช้ฟังก์ชัน summary() เพื่อแสดงข้อมูลสรุปของโมเดลการถดถอยที่เหมาะสม:

 #view summary of regression model
summary(model)

Call:
lm(formula = y ~ x, data = df)

Residuals:
    Min 1Q Median 3Q Max 
-4.4793 -0.9772 -0.4772 1.4388 4.6328 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 11.1432 1.9104 5.833 0.00039 ***
x 1.2780 0.2984 4.284 0.00267 ** 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.929 on 8 degrees of freedom
Multiple R-squared: 0.6964, Adjusted R-squared: 0.6584 
F-statistic: 18.35 on 1 and 8 DF, p-value: 0.002675

ต่อไปนี้เป็นวิธีตีความค่าที่สำคัญที่สุดในโมเดล:

• สถิติ F = 18.35, ค่า p ที่สอดคล้องกัน = 0.002675 เนื่องจากค่า p นี้น้อยกว่า 0.05 แบบจำลองโดยรวมจึงมีนัยสำคัญทางสถิติ
• หลาย R กำลังสอง = 0.6964 สิ่งนี้บอกเราว่า 69.64% ของการแปรผันในตัวแปรตอบสนอง y สามารถอธิบายได้ด้วยตัวแปรทำนาย x
• ค่าสัมประสิทธิ์โดยประมาณของ x : 1.2780 นี่บอกเราว่าการเพิ่มหน่วย x แต่ละครั้งสัมพันธ์กับการเพิ่มขึ้นเฉลี่ย 1.2780 ใน y

จากนั้นเราสามารถใช้การประมาณค่าสัมประสิทธิ์จากผลลัพธ์เพื่อเขียนสมการการถดถอยโดยประมาณ:

y = 11.1432 + 1.2780*(x)

โบนัส : คุณสามารถดูคำแนะนำฉบับสมบูรณ์เกี่ยวกับการตีความแต่ละค่าของเอาต์พุตการถดถอยใน R ได้ที่นี่

ดูแผนการวินิจฉัยโมเดล

จากนั้นเราสามารถใช้ฟังก์ชัน plot() เพื่อพล็อตแผนการวินิจฉัยของแบบจำลองการถดถอย:

 #create diagnostic plots
plot(model) 

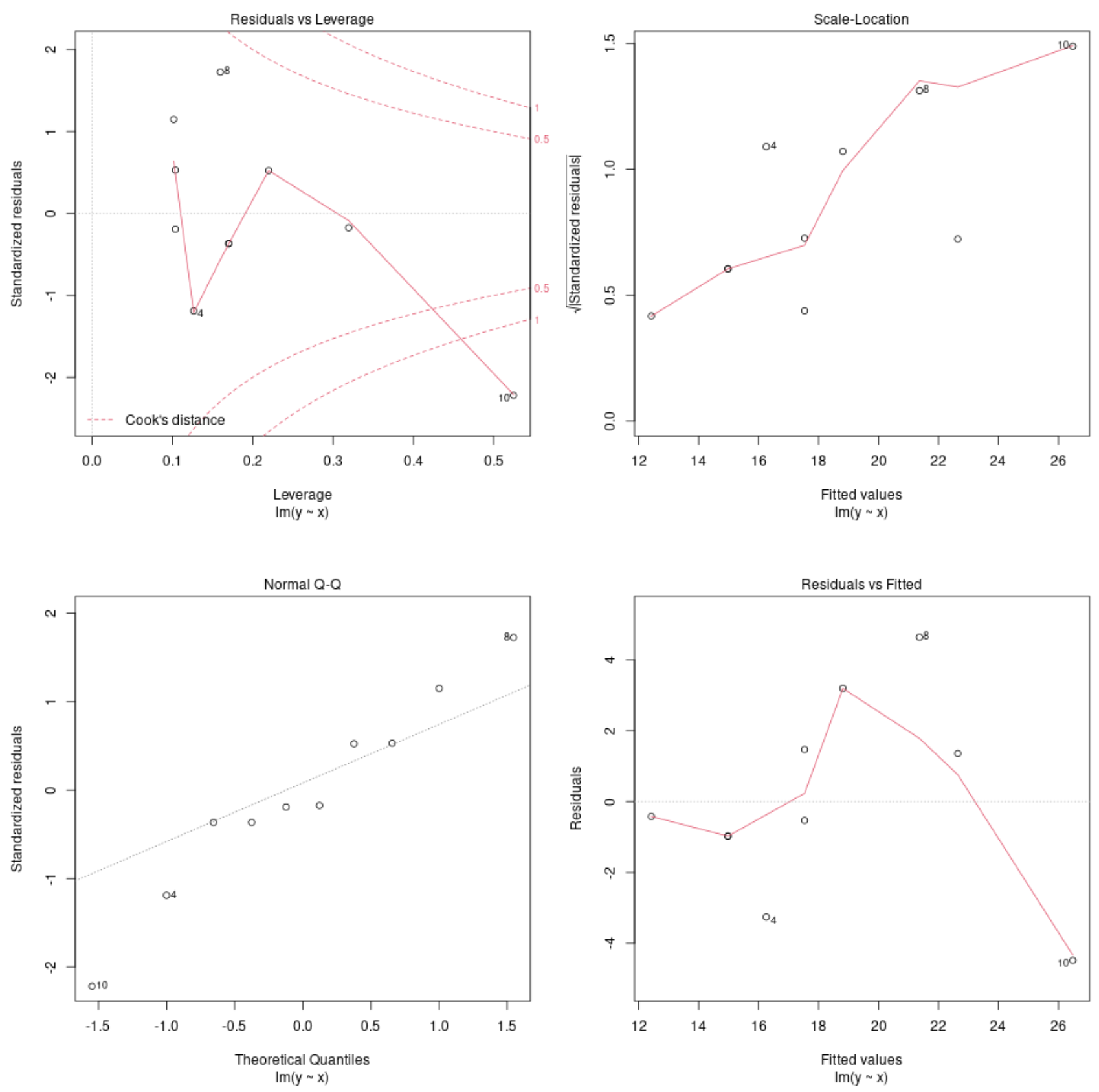
กราฟเหล่านี้ช่วยให้เราสามารถวิเคราะห์ ส่วนที่เหลือ ของแบบจำลองการถดถอยเพื่อพิจารณาว่าแบบจำลองนั้นเหมาะสมที่จะใช้กับข้อมูลหรือไม่

โปรดดู บทช่วยสอนนี้ สำหรับคำอธิบายที่สมบูรณ์เกี่ยวกับวิธีตีความแผนการวินิจฉัยของโมเดลใน R

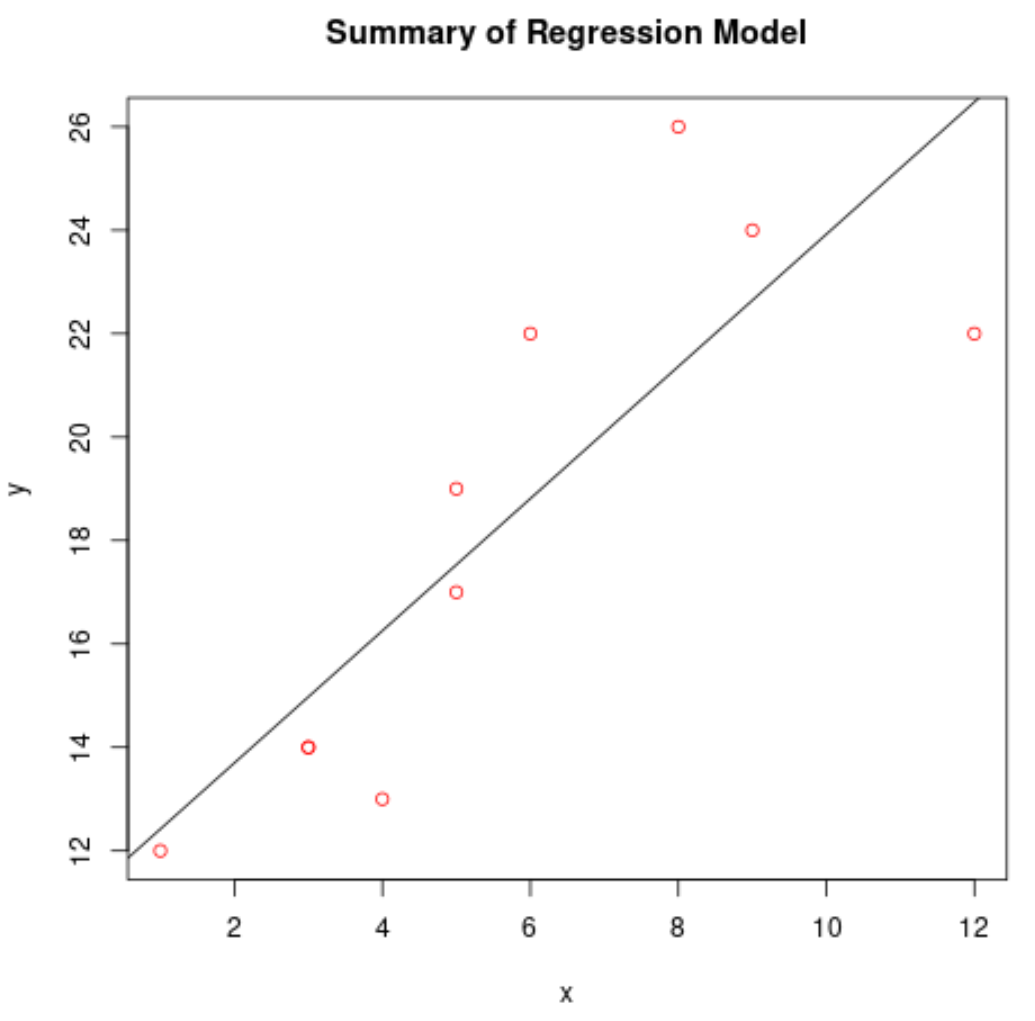
พล็อตโมเดลการถดถอยที่ติดตั้งไว้

เราสามารถใช้ฟังก์ชัน abline() เพื่อพล็อตโมเดลการถดถอยที่ติดตั้ง:

 #create scatterplot of raw data
plot(df$x, df$y, col=' red ', main=' Summary of Regression Model ', xlab=' x ', ylab=' y ')

#add fitted regression line
abline(model)

ใช้แบบจำลองการถดถอยเพื่อคาดการณ์

เราสามารถใช้ฟังก์ชัน Predict() เพื่อทำนายค่าการตอบสนองสำหรับการสังเกตใหม่:

 #define new observation
new <- data. frame (x=c(5))

#use the fitted model to predict the value for the new observation
predict(model, newdata = new)

      1 
17.5332

แบบจำลองคาดการณ์ว่าการสังเกตใหม่นี้จะมีค่าตอบสนองเป็น 17.5332

แหล่งข้อมูลเพิ่มเติม

วิธีดำเนินการถดถอยเชิงเส้นอย่างง่ายใน R
วิธีดำเนินการถดถอยเชิงเส้นพหุคูณใน R
วิธีการถดถอยแบบขั้นตอนใน R