วิธีใช้ fitdistr() ใน r เพื่อให้พอดีกับการแจกแจง

คุณสามารถใช้ฟังก์ชัน fitdistr() จากแพ็คเกจ MASS ใน R เพื่อประมาณค่าพารามิเตอร์ของการแจกแจงโดยการเพิ่มฟังก์ชันความน่าจะเป็นให้สูงสุด

ฟังก์ชันนี้ใช้ไวยากรณ์พื้นฐานต่อไปนี้:

fitdistr(x, หนาแน่นสนุก, …)

ทอง:

• x : เวกเตอร์ตัวเลขที่แสดงถึงค่าของการแจกแจง
• Densefun : การกระจายเพื่อประมาณค่าพารามิเตอร์

โปรดทราบว่าอาร์กิวเมนต์ Densefun ยอมรับชื่อการแจกแจงที่เป็นไปได้ต่อไปนี้: beta , cauchy , chi-square , exponential , gamma , Geometric , lognormal , logistic , Negative binomial , Normal , Poisson , t และ Weibull

ตัวอย่างต่อไปนี้แสดงวิธีการใช้ฟังก์ชัน fitdistr() ในทางปฏิบัติ

ตัวอย่าง: วิธีใช้ฟังก์ชัน fitdistr() เพื่อให้พอดีกับการแจกแจงใน R

สมมติว่าเราใช้ฟังก์ชัน rnorm() ใน R เพื่อสร้างเวกเตอร์ 200 ค่าที่เป็นไปตามการแจกแจงแบบปกติ:

 #make this example reproducible
set. seeds (1)

#generate sample of 200 observations that follows normal dist with mean=10 and sd=3
data <- rnorm(200, mean=10, sd=3)

#view first 6 observations in sample
head(data)

[1] 8.120639 10.550930 7.493114 14.785842 10.988523 7.538595

เราสามารถใช้ฟังก์ชัน hist() เพื่อสร้างฮิสโตแกรมเพื่อแสดงภาพการกระจายของค่าข้อมูล:

 hist(data, col=' steelblue ')

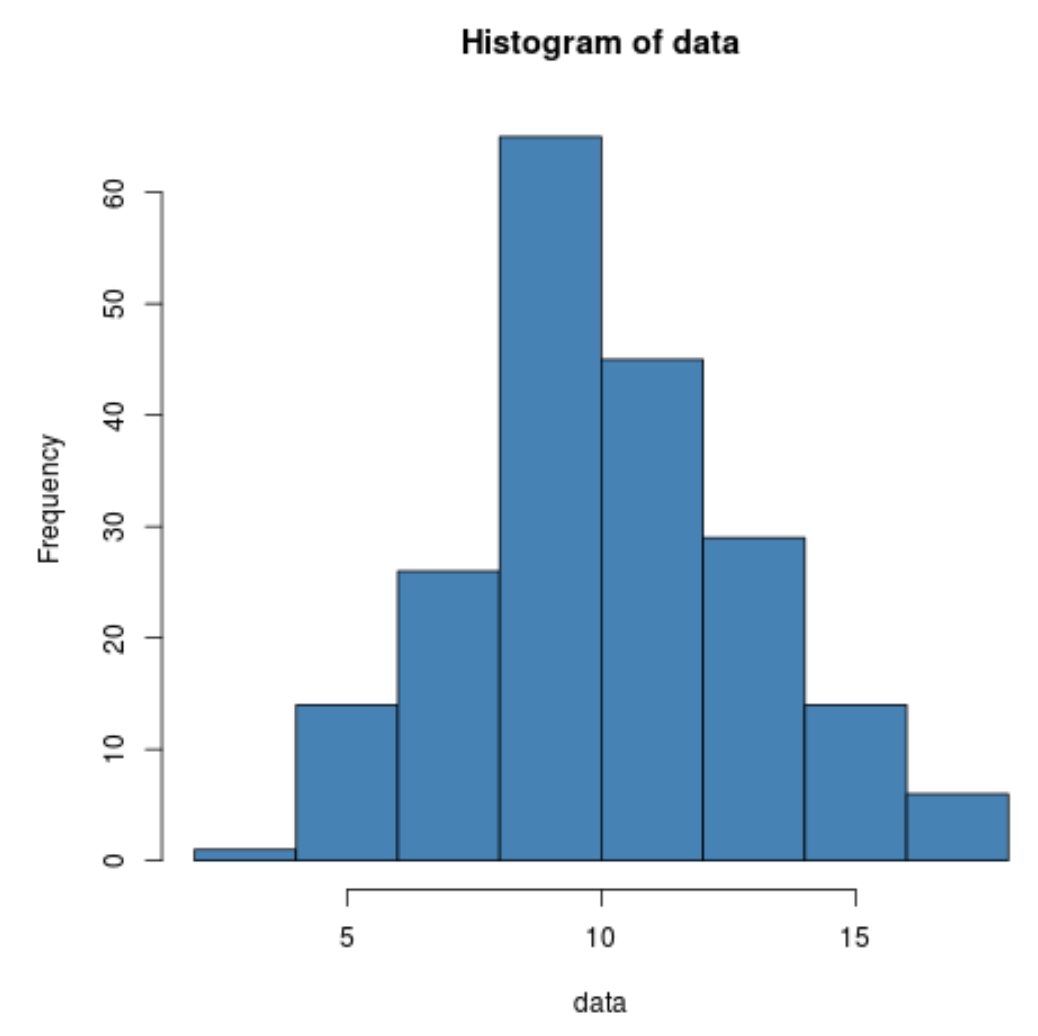
เราจะเห็นได้ว่าข้อมูลมีการกระจายแบบปกติจริงๆ

จากนั้นเราสามารถใช้ฟังก์ชัน fitdistr() เพื่อประมาณค่าพารามิเตอร์ของการแจกแจงนี้:

 library (MASS)

#estimate parameters of distribution
fitdistr(data, “ normal ”)

      mean sd    
  10.1066189 2.7803148 
 (0.1965979) (0.1390157)

ฟังก์ชัน fitdistr() ประมาณการว่าเวกเตอร์ของค่าเป็นไปตาม การแจกแจงแบบปกติ โดยมีค่าเฉลี่ย 10.1066189 และค่าเบี่ยงเบนมาตรฐาน 2.7803148

ค่าเหล่านี้ไม่ควรน่าแปลกใจเนื่องจากเราสร้างข้อมูลโดยใช้ฟังก์ชัน rnorm() โดยมีค่าเฉลี่ย 10 และค่าเบี่ยงเบนมาตรฐาน 3

แหล่งข้อมูลเพิ่มเติม

บทช่วยสอนต่อไปนี้จะอธิบายวิธีดำเนินการงานทั่วไปอื่นๆ ใน R:

วิธีการพล็อตการแจกแจงแบบปกติใน R
วิธีสร้างการแจกแจงแบบปกติใน R
วิธีทำการทดสอบ Shapiro-Wilk เพื่อความปกติใน R