ระดับเบต้าในสถิติคืออะไร? (คำจำกัดความ & #038; ตัวอย่าง)

ในสถิติ เราใช้ การทดสอบสมมติฐาน เพื่อพิจารณาว่าสมมติฐานเกี่ยวกับ พารามิเตอร์ประชากร เป็นจริงหรือไม่

การทดสอบสมมติฐานจะมีสมมติฐานสองข้อต่อไปนี้เสมอ:

สมมติฐานว่าง (H ₀ ): ข้อมูลตัวอย่างสอดคล้องกับความเชื่อหลักเกี่ยวกับพารามิเตอร์ประชากร

สมมติฐานทางเลือก ( _HA ): ข้อมูลตัวอย่างแสดงให้เห็นว่าสมมติฐานที่ระบุไว้ในสมมติฐานว่างนั้นไม่เป็นความจริง กล่าวอีกนัยหนึ่ง สาเหตุที่ไม่สุ่มส่งผลต่อข้อมูล

เมื่อใดก็ตามที่เราทำการทดสอบสมมติฐาน จะมีผลลัพธ์ที่เป็นไปได้สี่ประการเสมอ:

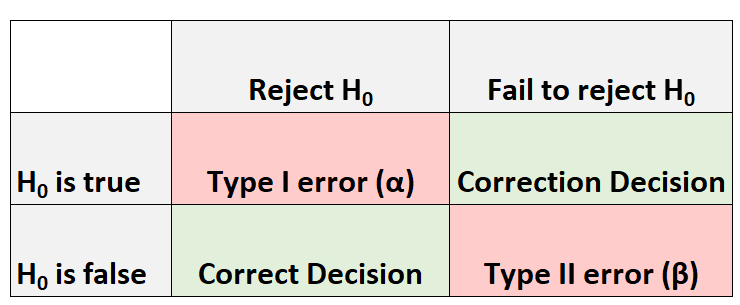
มีข้อผิดพลาดสองประเภทที่เราสามารถทำได้:

• ข้อผิดพลาดประเภทที่ 1: เราปฏิเสธสมมติฐานว่างเมื่อเป็นจริง ความน่าจะเป็นของข้อผิดพลาดประเภทนี้จะแสดงไว้ α .
• ข้อผิดพลาดประเภท II: เราไม่สามารถปฏิเสธสมมติฐานว่างได้ เมื่อเป็นจริงแล้วเป็นเท็จ ความน่าจะเป็นของข้อผิดพลาดประเภทนี้จะถูกบันทึกไว้ β

ความสัมพันธ์ระหว่างอัลฟ่าและเบต้า

ตามหลักการแล้ว นักวิจัยต้องการความน่าจะเป็นที่จะเกิดข้อผิดพลาดประเภทที่ 1 และ ความน่าจะเป็นที่จะทำให้เกิดข้อผิดพลาดประเภทที่ 2 นั้นต่ำ

อย่างไรก็ตาม มีการประนีประนอมระหว่างความน่าจะเป็นทั้งสองนี้ หากเราลดระดับอัลฟ่า เราอาจลดความน่าจะเป็นที่จะปฏิเสธสมมติฐานว่างเมื่อเป็นจริง แต่จะเพิ่มระดับเบต้าลงไป ความน่าจะเป็นที่เราไม่สามารถปฏิเสธสมมติฐานว่างเมื่อมันผิด

ความสัมพันธ์ระหว่างอำนาจและเบต้า

พลัง ของการทดสอบสมมติฐานหมายถึงความน่าจะเป็นในการตรวจจับผลกระทบหรือความแตกต่างเมื่อมีผลกระทบหรือความแตกต่างเกิดขึ้นจริง กล่าวอีกนัยหนึ่ง มันคือความน่าจะเป็นที่จะปฏิเสธสมมติฐานว่างที่เป็นเท็จได้อย่างถูกต้อง

มีการคำนวณดังนี้:

กำลัง = 1 – β

โดยทั่วไปแล้ว นักวิจัยต้องการให้พลังของการทดสอบอยู่ในระดับสูง เพื่อว่าหากมีผลกระทบหรือความแตกต่าง การทดสอบจะสามารถตรวจจับได้

จากสมการข้างต้น เราจะเห็นได้ว่าวิธีที่ดีที่สุดในการเพิ่มพลังของการทดสอบคือการลดระดับเบต้า และวิธีที่ดีที่สุดในการลดระดับเบต้าคือการเพิ่มขนาดตัวอย่าง

ตัวอย่างต่อไปนี้แสดงวิธีคำนวณระดับเบต้าของการทดสอบสมมติฐาน และแสดงให้เห็นว่าเหตุใดการเพิ่มขนาดตัวอย่างจึงสามารถลดระดับเบต้าได้

ตัวอย่างที่ 1: คำนวณเบต้าสำหรับการทดสอบสมมติฐาน

สมมติว่านักวิจัยต้องการทดสอบว่าน้ำหนักเฉลี่ยของวิดเจ็ตที่ผลิตในโรงงานน้อยกว่า 500 ออนซ์หรือไม่ เรารู้ว่าค่าเบี่ยงเบนมาตรฐานของน้ำหนักคือ 24 ออนซ์ และนักวิจัยตัดสินใจสุ่มตัวอย่างวิดเจ็ต 40 ชิ้น

มันจะตระหนักถึงสมมติฐานต่อไปนี้ที่ α = 0.05:

• ชม ₀ : µ = 500
• _HA : μ < 500

ตอนนี้ลองจินตนาการว่าน้ำหนักเฉลี่ยของวิดเจ็ตที่ผลิตได้จริงอยู่ที่ 490 ออนซ์ กล่าวอีกนัยหนึ่ง สมมติฐานว่างจะต้องถูกปฏิเสธ

เราสามารถใช้ขั้นตอนต่อไปนี้เพื่อคำนวณระดับเบต้า – ความน่าจะเป็นที่จะไม่ปฏิเสธสมมติฐานว่าง ทั้งที่ความจริงแล้วควรถูกปฏิเสธ:

ขั้นตอนที่ 1: ค้นหาภูมิภาคที่ไม่มีการปฏิเสธ

จากเครื่องคำนวณค่า Z วิกฤต ค่าวิกฤตด้านซ้ายที่ α = 0.05 คือ -1.645

ขั้นตอนที่ 2: ค้นหาตัวอย่างขั้นต่ำที่เราไม่สามารถปฏิเสธได้

สถิติการทดสอบคำนวณเป็น z = ( x – μ) / (s/ √n )

ดังนั้น เราสามารถแก้สมการนี้เพื่อหาค่าเฉลี่ยตัวอย่างได้:

• x = µ – z*(s/ √n )
• x = 500 – 1.645*(24/ √40 )
• x = 493.758

ขั้นตอนที่ 3: กำหนดความน่าจะเป็นที่ค่าเฉลี่ยตัวอย่างขั้นต่ำจะเกิดขึ้นจริง

เราสามารถคำนวณความน่าจะเป็นนี้ได้ดังนี้:

• P(Z ≥ (493.758 – 490) / (24/√ 40 ))
• P(แซด ≥ 0.99)

ตาม เครื่องคิดเลข CDF ปกติ ความน่าจะเป็นที่ Z ≥ 0.99 คือ 0.1611

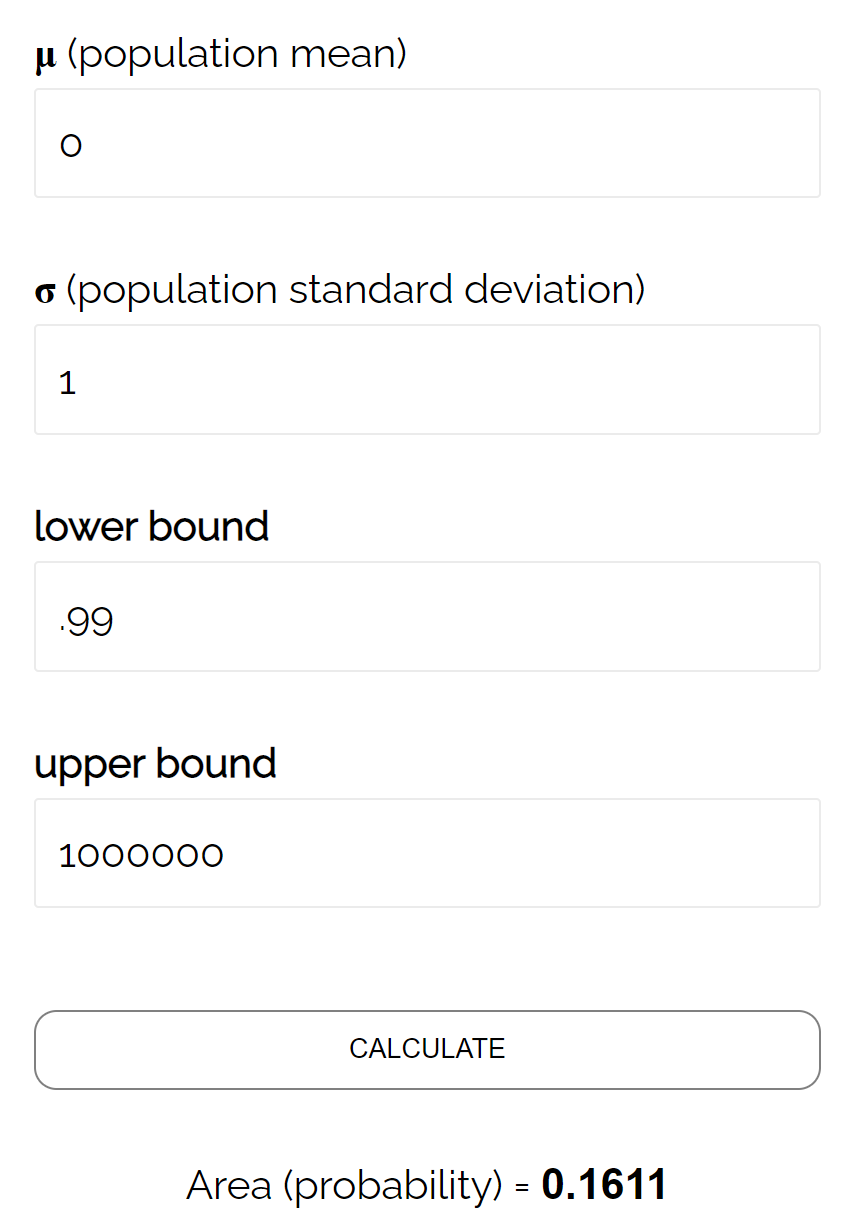
ดังนั้นระดับเบต้าสำหรับการทดสอบนี้คือ β = 0.1611 ซึ่งหมายความว่ามีโอกาส 16.11% ที่จะไม่พบความแตกต่างหากค่าเฉลี่ยจริงคือ 490 ออนซ์

ตัวอย่างที่ 2: คำนวณเบต้าสำหรับการทดสอบด้วยขนาดตัวอย่างที่ใหญ่ขึ้น

ตอนนี้ สมมติว่าผู้วิจัยทำการทดสอบสมมติฐานเดียวกันทุกประการ แต่ใช้ตัวอย่างวิดเจ็ต n = 100 ชิ้นแทน เราสามารถทำซ้ำสามขั้นตอนเดียวกันนี้เพื่อคำนวณระดับเบต้าสำหรับการทดสอบนี้:

ขั้นตอนที่ 1: ค้นหาภูมิภาคที่ไม่มีการปฏิเสธ

จากเครื่องคำนวณค่า Z วิกฤต ค่าวิกฤตด้านซ้ายที่ α = 0.05 คือ -1.645

ขั้นตอนที่ 2: ค้นหาตัวอย่างขั้นต่ำที่เราไม่สามารถปฏิเสธได้

สถิติการทดสอบคำนวณเป็น z = ( x – μ) / (s/ √n )

ดังนั้น เราสามารถแก้สมการนี้เพื่อหาค่าเฉลี่ยตัวอย่างได้:

• x = µ – z*(s/ √n )
• x = 500 – 1.645*(24/√ 100 )
• x = 496.05

ขั้นตอนที่ 3: กำหนดความน่าจะเป็นที่ค่าเฉลี่ยตัวอย่างขั้นต่ำจะเกิดขึ้นจริง

เราสามารถคำนวณความน่าจะเป็นนี้ได้ดังนี้:

• P(Z ≥ (496.05 – 490) / (24/√ 100 ))
• P(Z ≥ 2.52)

ตาม เครื่องคิดเลข CDF ปกติ ความน่าจะเป็นที่ Z ≥ 2.52 คือ 0.0059

ดังนั้น ระดับเบต้าสำหรับการทดสอบนี้คือ β = 0.0059 ซึ่งหมายความว่ามีโอกาสเพียง 0.59% เท่านั้นที่จะไม่พบความแตกต่างหากค่าเฉลี่ยจริงคือ 490 ออนซ์

โปรดทราบว่าเพียงเพิ่มขนาดตัวอย่างจาก 40 เป็น 100 ผู้วิจัยก็สามารถลดระดับเบต้าจาก 0.1611 เป็น 0.0059 ได้

โบนัส: ใช้เครื่องคำนวณข้อผิดพลาด Type II เพื่อคำนวณระดับเบต้าของการทดสอบโดยอัตโนมัติ

แหล่งข้อมูลเพิ่มเติม

ความรู้เบื้องต้นเกี่ยวกับการทดสอบสมมติฐาน
วิธีการเขียนสมมติฐานว่าง (5 ตัวอย่าง)
คำอธิบายค่า P และนัยสำคัญทางสถิติ