แปลงที่เหลือดีหรือไม่ดีเรียกว่าอะไร?

ในการวิเคราะห์การถดถอย พล็อตส่วนที่เหลือ คือพล็อตประเภทหนึ่งที่แสดงค่าที่พอดีของแบบจำลองการถดถอยบนแกน x และส่วนที่เหลือของแบบจำลองตามแนวแกน y

เมื่อตรวจสอบเค้าโครงที่เหลือด้วยสายตา โดยทั่วไปเราจะมองหาสองสิ่งเพื่อพิจารณาว่าเค้าโครงนั้น “ดี” หรือ “ไม่ดี”:

1. ยอดคงเหลือมีแนวโน้มชัดเจนหรือไม่?

• ในแปลงซากที่ “ดี” ซากที่เหลือไม่แสดงแนวโน้มที่ชัดเจน
• ในแผนซากที่ “ไม่ดี” สิ่งตกค้างจะมีรูปแบบบางประเภท เช่น เส้นโค้งหรือคลื่น สิ่งนี้บ่งชี้ว่าแบบจำลองการถดถอยที่เราใช้ไม่ได้ให้ความเหมาะสมกับข้อมูล

2. ปริมาณคงเหลือเพิ่มขึ้นหรือลดลงของความแปรปรวนอย่างเป็นระบบหรือไม่?

• ในพล็อตส่วนที่เหลือที่ “ดี” ส่วนที่เหลือจะถูกสุ่มกระจัดกระจายรอบศูนย์โดยไม่มีการเพิ่มหรือลดความแปรปรวนอย่างเป็นระบบ
• ในแผนสารตกค้างที่ “ไม่ดี” ความแปรปรวนของสารตกค้างจะเพิ่มขึ้นหรือลดลงอย่างเป็นระบบ

หากแปลงส่วนที่เหลือได้รับการจัดอันดับ “ดี” หมายความว่าเราสามารถเชื่อถือผลลัพธ์ของแบบจำลองการถดถอยได้ และจะปลอดภัยในการตีความค่าสัมประสิทธิ์ของแบบจำลอง

อย่างไรก็ตาม หากพล็อตส่วนที่เหลือได้รับการจัดอันดับ “แย่” นั่นหมายความว่าผลลัพธ์ของแบบจำลองไม่น่าเชื่อถือ และเราจำเป็นต้องปรับแบบจำลองการถดถอยอื่นให้พอดีกับข้อมูล

ตัวอย่างต่อไปนี้จะอธิบายวิธีตีความแปลงที่ดินที่ “ดี” และ “ไม่ดี” ในทางปฏิบัติ

ตัวอย่างที่ 1: ร่องรอยตกค้าง “ดี”

สมมติว่าเราใส่แบบจำลองการถดถอยและได้แผนภาพที่เหลือดังต่อไปนี้:

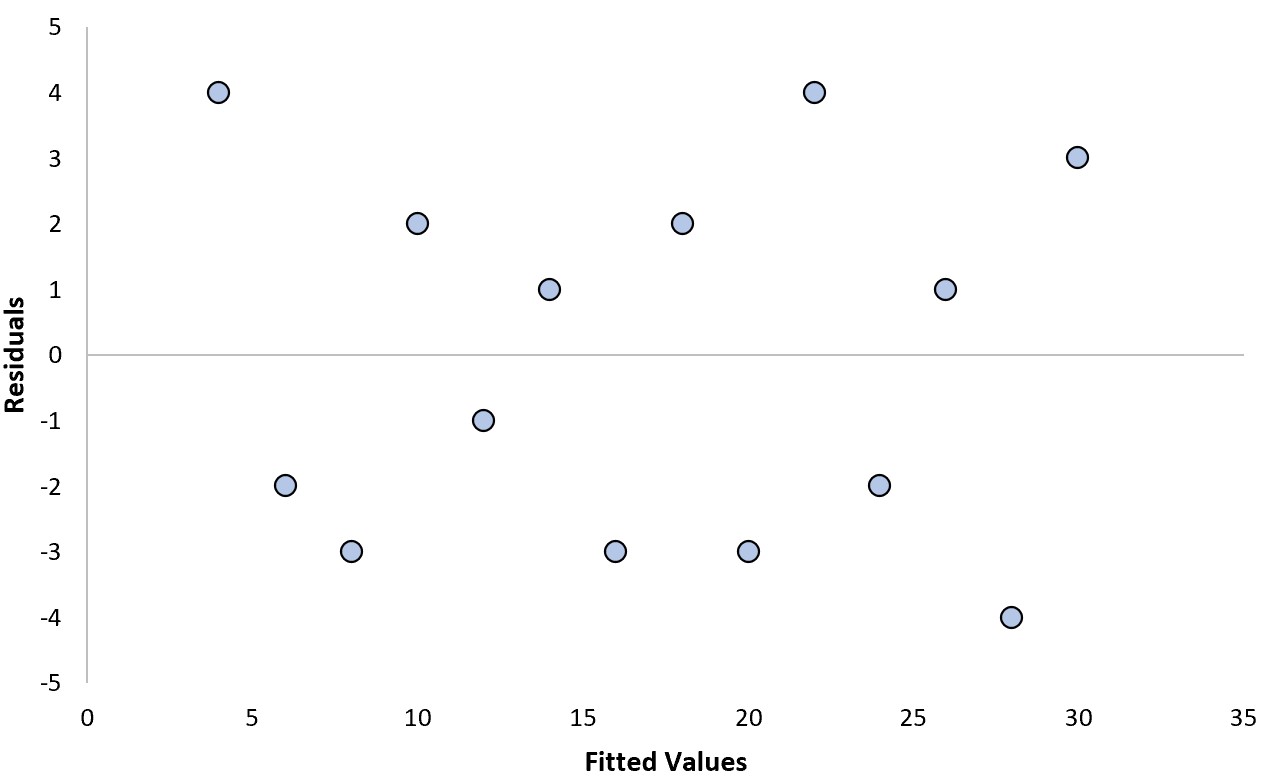
เราสามารถตอบคำถามสองข้อต่อไปนี้เพื่อพิจารณาว่านี่เป็นพล็อตที่เหลือ “ดี” หรือไม่:

1. ยอดคงเหลือมีแนวโน้มชัดเจนหรือไม่?

ไม่ ส่วนที่เหลือจะกระจัดกระจายแบบสุ่มรอบๆ ศูนย์ โดยไม่มีรูปแบบที่ชัดเจน

2. ปริมาณคงเหลือเพิ่มขึ้นหรือลดลงของความแปรปรวนอย่างเป็นระบบหรือไม่?

ไม่ สารตกค้างมีความแปรปรวนค่อนข้างคงที่ (เช่น ระยะห่างระหว่างสารตกค้างและค่าศูนย์) ในแต่ละระดับของค่าที่ติดตั้ง

เนื่องจากเราตอบว่า “ไม่” สำหรับคำถามทั้งสองข้อนี้ เราจะถือว่านี่เป็นแปลงที่เหลือ “ดี”

ดังนั้นเราจึงสามารถเชื่อถือผลลัพธ์ของแบบจำลองการถดถอยและตีความค่าสัมประสิทธิ์แบบจำลองได้อย่างปลอดภัย

ตัวอย่างที่ 2: พล็อตส่วนที่เหลือ “ไม่ดี” พร้อมแบบจำลองที่ชัดเจน

สมมติว่าเราใส่แบบจำลองการถดถอยและได้แผนภาพที่เหลือดังต่อไปนี้:

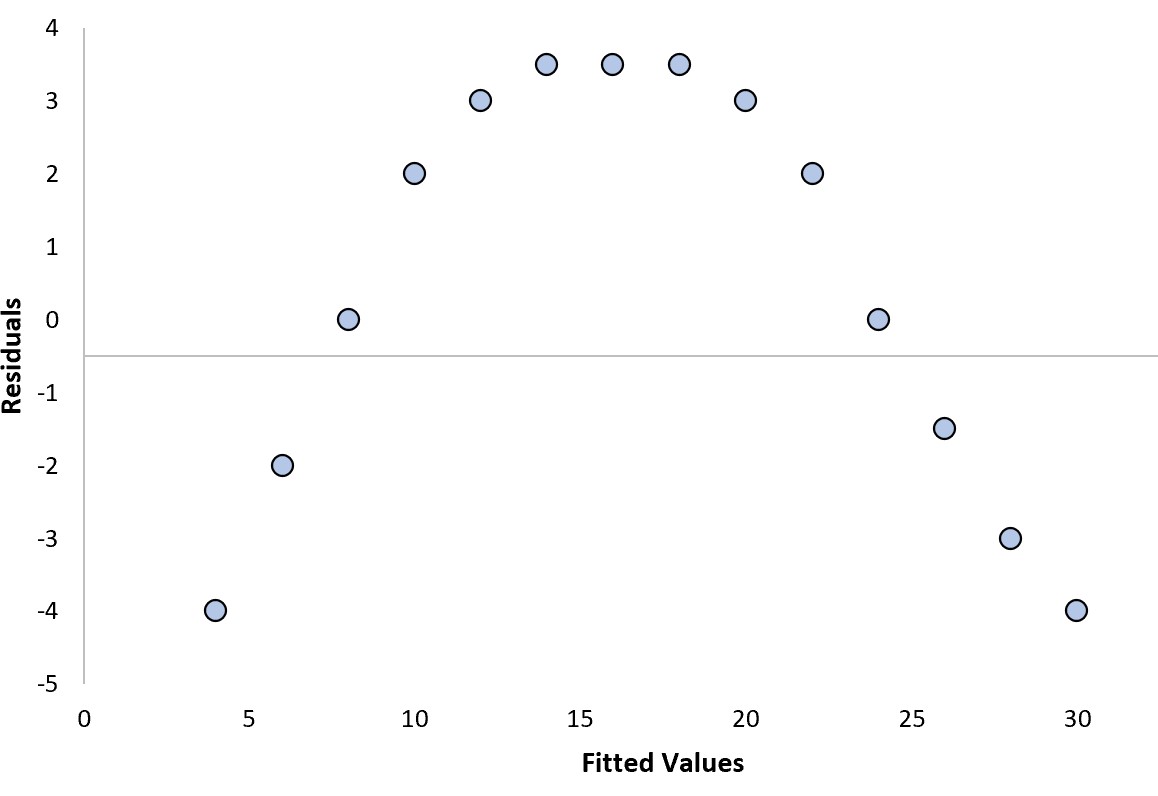
เราสามารถตอบคำถามสองข้อต่อไปนี้เพื่อพิจารณาว่านี่เป็นพล็อตที่เหลือ “ดี” หรือไม่:

1. ยอดคงเหลือมีแนวโน้มชัดเจนหรือไม่?

ใช่ . สารตกค้างแสดงรูปแบบโค้ง

2. ปริมาณคงเหลือเพิ่มขึ้นหรือลดลงของความแปรปรวนอย่างเป็นระบบหรือไม่?

ใช่ . สารตกค้างจะมีระดับความแปรปรวนต่างกันในระดับต่างๆ ของค่าที่ติดตั้ง

เนื่องจากเราตอบว่า “ใช่” อย่างน้อยหนึ่งคำถาม เราจะถือว่านี่เป็นโครงเรื่องที่ “ไม่ดี”

ซึ่งหมายความว่าแบบจำลองการถดถอยไม่เหมาะกับข้อมูล

โดยเฉพาะอย่างยิ่ง รูปแบบโค้ง ในแผนภาพส่วนที่เหลือบ่งชี้ว่าแบบจำลองการถดถอยเชิงเส้นไม่พอดีกับข้อมูล และแบบจำลองการถดถอยกำลังสองน่าจะทำงานได้ดีกว่า

ตัวอย่างที่ 3: พล็อตที่เหลือ “ไม่ดี” ที่มีความแปรปรวนเพิ่มขึ้น

สมมติว่าเราใส่แบบจำลองการถดถอยและได้แผนภาพที่เหลือดังต่อไปนี้:

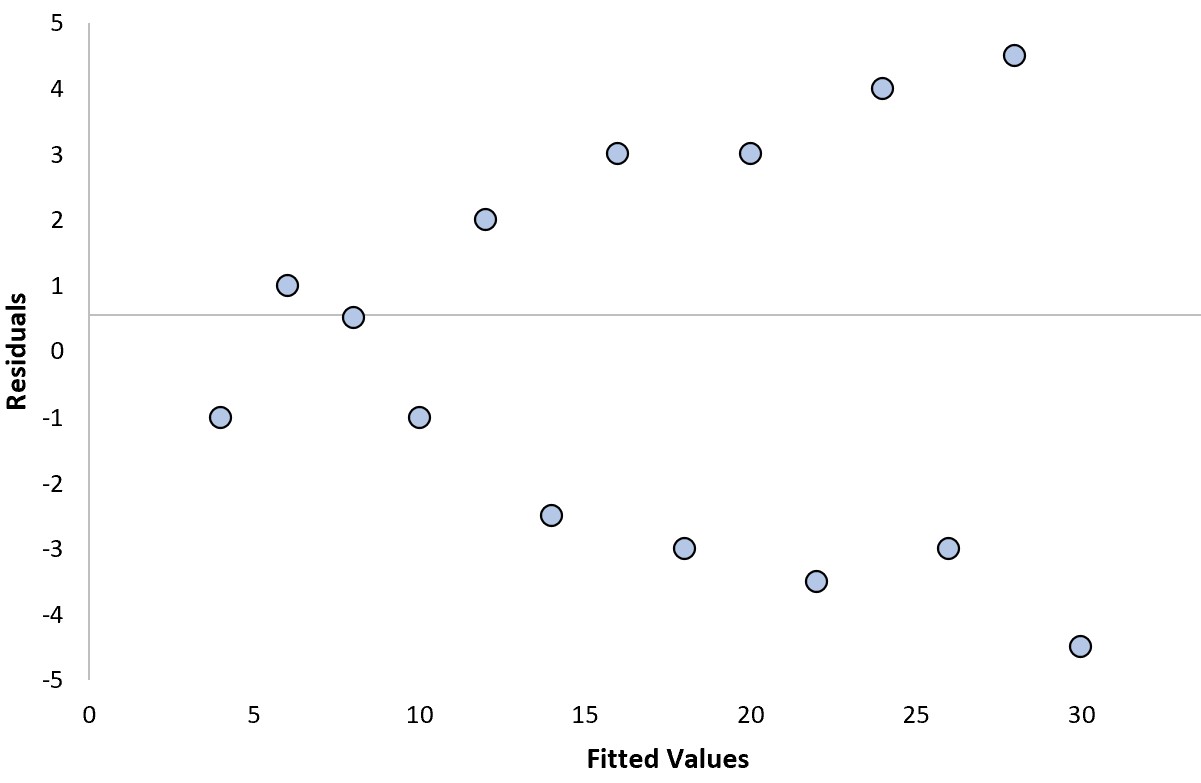
เราสามารถตอบคำถามสองข้อต่อไปนี้เพื่อพิจารณาว่านี่เป็นพล็อตที่เหลือ “ดี” หรือไม่:

1. ยอดคงเหลือมีแนวโน้มชัดเจนหรือไม่?

ไม่ใช่ ยังไม่มีแนวโน้มปริมาณคงเหลือที่ชัดเจน

2. ปริมาณคงเหลือเพิ่มขึ้นหรือลดลงของความแปรปรวนอย่างเป็นระบบหรือไม่?

ใช่ . ความแปรปรวนของสิ่งตกค้างจะเพิ่มขึ้นเมื่อค่าที่ติดตั้งเพิ่มขึ้น

เนื่องจากเราตอบว่า “ใช่” อย่างน้อยหนึ่งคำถาม เราจะถือว่านี่เป็นโครงเรื่องที่ “ไม่ดี”

ในตัวอย่างนี้ ปริมาณคงเหลือต้องทนทุกข์ทรมานจาก ความต่างกัน ซึ่งหมายถึงความแปรปรวนไม่เท่ากันของปริมาณคงเหลือในระดับต่างๆ ของค่าที่พอดี

ซึ่งหมายความว่าผลลัพธ์ของแบบจำลองการถดถอยอาจไม่น่าเชื่อถือ

ดู บทความนี้ เพื่อเรียนรู้วิธีต่างๆ ในการแก้ปัญหาความต่างกันในแบบจำลองการถดถอย

แหล่งข้อมูลเพิ่มเติม

บทช่วยสอนต่อไปนี้จะอธิบายวิธีสร้างแปลงที่เหลือโดยใช้ซอฟต์แวร์ทางสถิติต่างๆ:

วิธีสร้างพล็อตที่เหลือใน R
วิธีสร้างพล็อตที่เหลือใน Python
วิธีการสร้างพล็อตที่เหลือใน Excel
วิธีสร้างพล็อตคงเหลือใน SAS