วิธีการตีความพล็อตส่วนที่เหลือแบบโค้ง (พร้อมตัวอย่าง)

แปลงที่เหลือใช้ เพื่อประเมินว่า ส่วนที่เหลือ ของแบบจำลองการถดถอยมีการกระจายตามปกติหรือไม่ และพวกมันแสดง ความแตกต่างกัน หรือไม่

ตามหลักการแล้ว คุณต้องการให้จุดต่างๆ ในพล็อตที่เหลือกระจายแบบสุ่มรอบๆ ค่าศูนย์ โดยไม่มีรูปแบบที่ชัดเจน

หากคุณพบพล็อตที่เหลือซึ่งจุดพล็อตมีรูปแบบโค้ง อาจหมายความว่าแบบจำลองการถดถอยที่คุณระบุสำหรับข้อมูลไม่ถูกต้อง

ในกรณีส่วนใหญ่ หมายความว่าคุณได้พยายามปรับแบบจำลองการถดถอยเชิงเส้นให้พอดีกับชุดข้อมูลที่เป็นไปตามแนวโน้มกำลังสองแทน

ตัวอย่างต่อไปนี้แสดงวิธีตีความ (และแก้ไข) แผนภาพส่วนโค้งที่เหลือในทางปฏิบัติ

ตัวอย่าง: การตีความแปลงส่วนโค้งที่เหลือ

สมมติว่าเรารวบรวมข้อมูลต่อไปนี้เกี่ยวกับจำนวนชั่วโมงทำงานต่อสัปดาห์ และรายงานระดับความสุข (ในระดับ 0 ถึง 100) สำหรับคน 11 คนในสำนักงาน:

หากเราสร้างแผนกระจายชั่วโมงการทำงานเทียบกับระดับความสุขอย่างง่าย มันจะเป็นดังนี้:

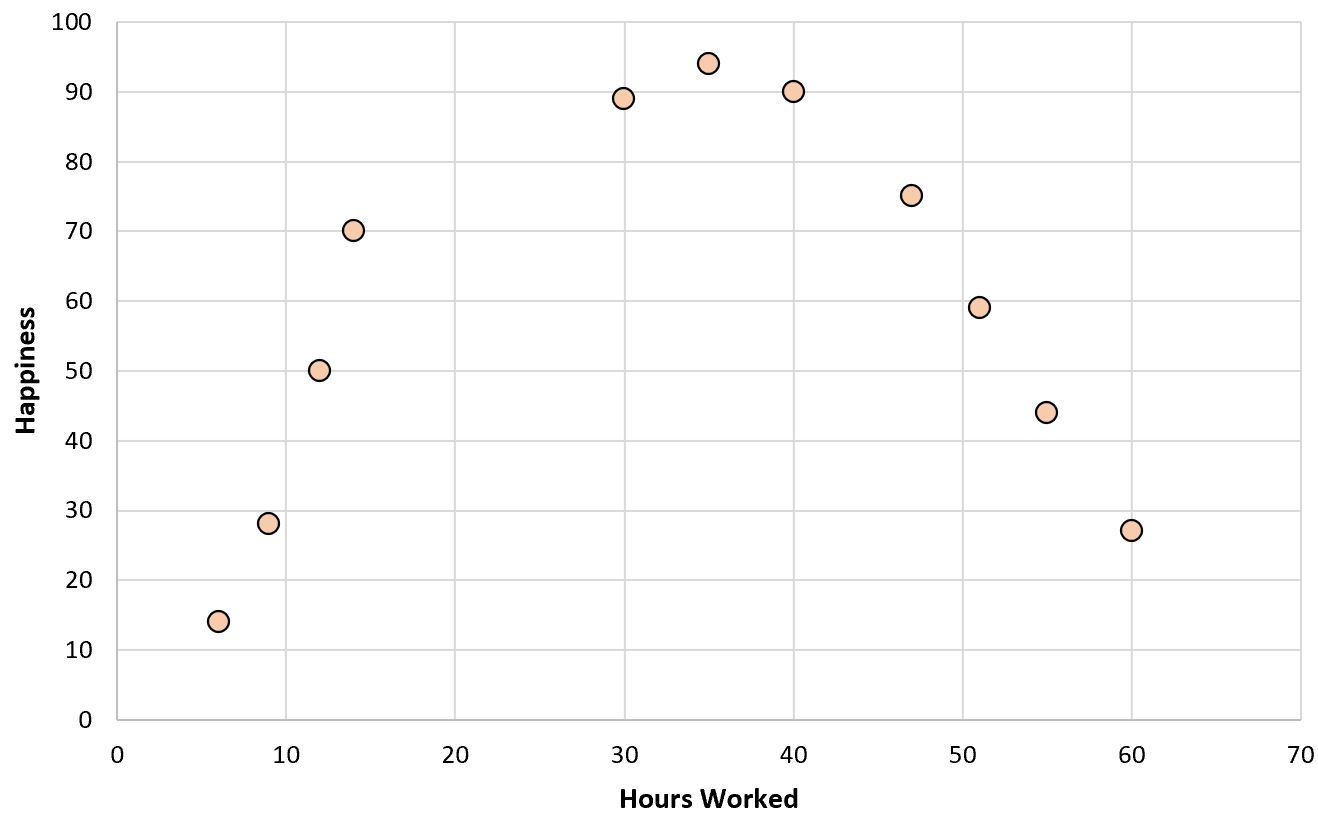
ทีนี้ สมมติว่าเราต้องการสร้างแบบจำลองการถดถอยโดยใช้ชั่วโมงทำงานเพื่อทำนายระดับความสุข

โค้ดต่อไปนี้แสดงวิธีปรับ โมเดลการถดถอยเชิงเส้นอย่างง่าย ให้เข้ากับชุดข้อมูลนี้และสร้างพล็อตส่วนที่เหลือใน R:

 #create dataframe
df <- data. frame (hours=c(6, 9, 12, 14, 30, 35, 40, 47, 51, 55, 60),
                 happiness=c(14, 28, 50, 70, 89, 94, 90, 75, 59, 44, 27))
#fit linear regression model
linear_model <- lm(happiness ~ hours, data=df)

#get list of residuals 
res <- resid(linear_model)

#produce residual vs. fitted plot
plot(fitted(linear_model), res, xlab=' Fitted Values ', ylab=' Residuals ')

#add a horizontal line at 0 
abline(0,0)

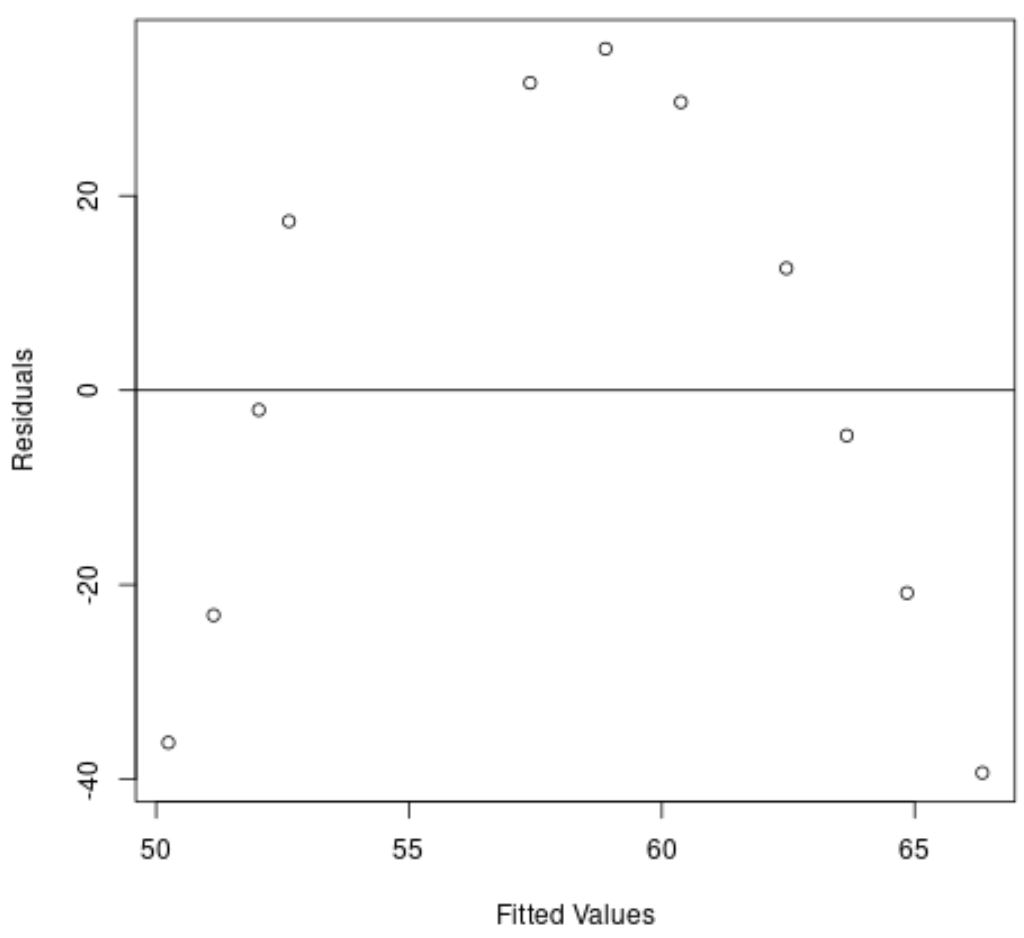
แกน x จะแสดงค่าที่พอดี และแกน y จะแสดงค่าคงเหลือ

จากกราฟ เราจะเห็นได้ว่ามีรูปแบบโค้งในส่วนที่เหลือ ซึ่งบ่งชี้ว่าแบบจำลองการถดถอยเชิงเส้นไม่ได้ให้ความพอดีที่เหมาะสมกับชุดข้อมูลนี้

รหัสต่อไปนี้แสดงวิธีปรับ โมเดลการถดถอยกำลังสอง ให้พอดีกับชุดข้อมูลนี้และสร้างพล็อตส่วนที่เหลือใน R:

 #create dataframe
df <- data. frame (hours=c(6, 9, 12, 14, 30, 35, 40, 47, 51, 55, 60),
                 happiness=c(14, 28, 50, 70, 89, 94, 90, 75, 59, 44, 27))
#define quadratic term to use in model
df$hours2 <- df$hours^2

#fit quadratic regression model
quadratic_model <- lm(happiness ~ hours + hours2, data=df)

#get list of residuals 
res <- resid(quadratic_model)

#produce residual vs. fitted plot
plot(fitted(quadratic_model), res, xlab=' Fitted Values ', ylab=' Residuals ')

#add a horizontal line at 0 
abline(0,0) 

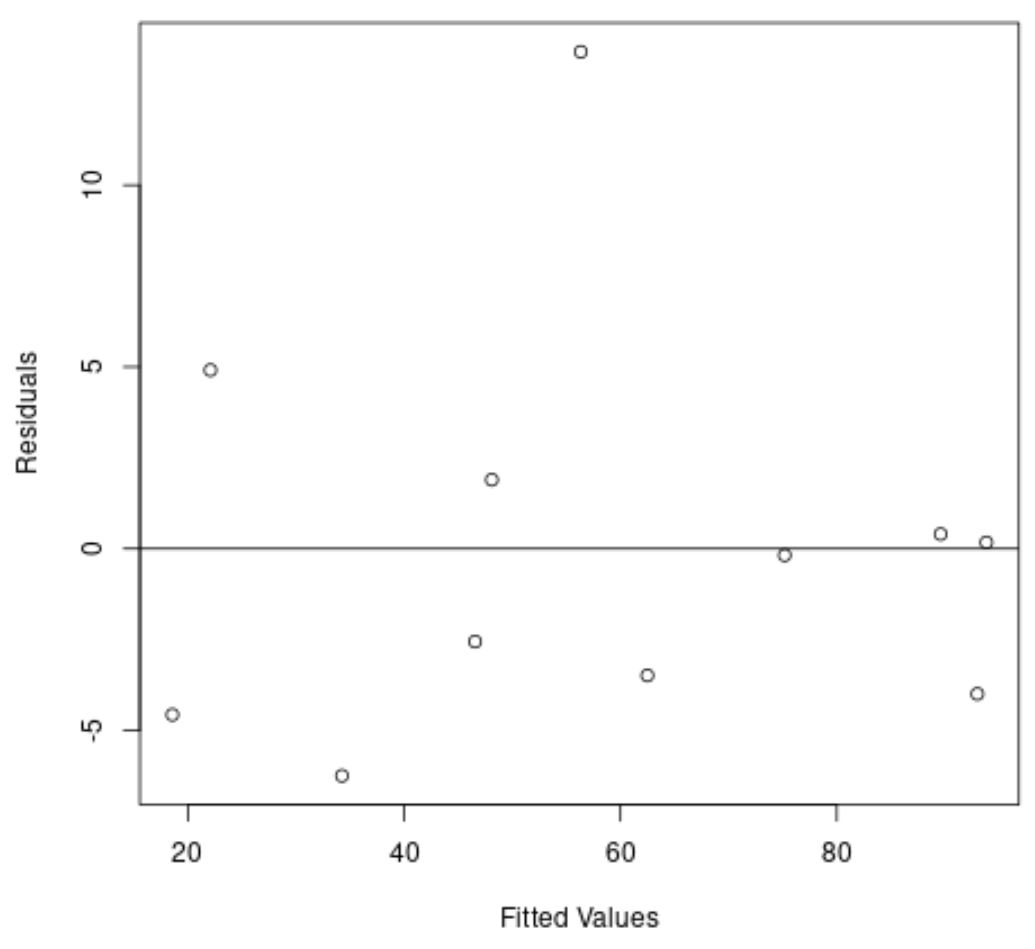
อีกครั้งที่แกน x จะแสดงค่าที่พอดีและแกน y จะแสดงค่าคงเหลือ

จากแผนภาพเราจะเห็นว่าสารตกค้างจะกระจัดกระจายแบบสุ่มรอบๆ ศูนย์ และไม่มีแนวโน้มที่ชัดเจนในสารตกค้าง

สิ่งนี้บอกเราว่าแบบจำลองการถดถอยกำลังสองทำงานได้ดีกว่าแบบจำลองการถดถอยเชิงเส้นได้ดีกว่ามาก

สิ่งนี้น่าจะสมเหตุสมผลเมื่อเราเห็นว่าความสัมพันธ์ที่แท้จริงระหว่างชั่วโมงทำงานกับระดับความสุขดูเหมือนจะเป็นแบบกำลังสองมากกว่าเชิงเส้น

แหล่งข้อมูลเพิ่มเติม

บทช่วยสอนต่อไปนี้จะอธิบายวิธีสร้างแปลงที่เหลือโดยใช้ซอฟต์แวร์ทางสถิติต่างๆ:

วิธีสร้างเส้นทางตกค้างด้วยมือ
วิธีสร้างพล็อตที่เหลือใน R
วิธีการสร้างพล็อตที่เหลือใน Excel
วิธีสร้างพล็อตที่เหลือใน Python