การวัดแนวโน้มจากส่วนกลาง: คำจำกัดความและตัวอย่าง
การวัดแนวโน้มจากศูนย์กลาง คือค่าเดียวที่แสดงถึงจุดศูนย์กลางของชุดข้อมูล ค่านี้สามารถเรียกได้ว่าเป็น “ตำแหน่งศูนย์กลาง” ของชุดข้อมูล
ในทางสถิติ มีมาตรการทั่วไปสามประการสำหรับแนวโน้มศูนย์กลาง:
- เฉลี่ย
- ค่ามัธยฐาน
- แฟชั่น
แต่ละการวัดเหล่านี้จะค้นหาตำแหน่งศูนย์กลางของชุดข้อมูลโดยใช้วิธีการที่แตกต่างกัน ขึ้นอยู่กับประเภทของข้อมูลที่คุณกำลังวิเคราะห์ อาจเป็นการดีกว่าถ้าใช้หนึ่งในสามเมตริกนี้ แทนที่จะใช้อีกสองเมตริกที่เหลือ
ในบทความนี้ เราจะดูวิธีคำนวณการวัดแนวโน้มส่วนกลางแต่ละค่าจากทั้งสามค่า ตลอดจนวิธีพิจารณาว่าการวัดใดเหมาะที่สุดที่จะใช้โดยพิจารณาจากข้อมูลของคุณ
เหตุใดการวัดแนวโน้มส่วนกลางจึงมีประโยชน์
ก่อนที่เราจะดูวิธีคำนวณค่าเฉลี่ย ค่ามัธยฐาน และโหมด ควรทำความเข้าใจ ว่าทำไม การวัดเหล่านี้จึงมีประโยชน์ตั้งแต่แรก
พิจารณาสถานการณ์ต่อไปนี้:
คู่รักหนุ่มสาวคู่หนึ่งกำลังตัดสินใจว่าจะซื้อบ้านหลังแรกในเมืองใหม่ได้ที่ไหน และจำนวนเงินสูงสุดที่พวกเขาสามารถใช้ได้คือ 150,000 ดอลลาร์ บางพื้นที่ของเมืองมีบ้านราคาแพง บางพื้นที่มีบ้านราคาถูก และบางพื้นที่มีบ้านราคาปานกลาง พวกเขาต้องการจำกัดการค้นหาให้แคบลงให้เหลือเฉพาะย่านใกล้เคียงที่เหมาะกับงบประมาณของตนได้อย่างง่ายดาย
หากคู่รักเพียงแค่ดูราคาบ้านเดี่ยวในแต่ละละแวกนั้น ก็อาจจะตัดสินใจได้ยากว่าย่านไหนที่เหมาะกับงบประมาณของตนมากที่สุด เพราะพวกเขาอาจเห็นดังนี้
ราคาบ้านในบริเวณใกล้เคียง A : $140,000, $190,000, $265,000, $115,000, $270,000, $240,000, $250,000, $180,000, $160,000, $200,000, $240,000, $280,000,…
ราคาบ้านในบริเวณใกล้เคียง B : 140,000 ดอลลาร์, 290,000 ดอลลาร์, 155,000 ดอลลาร์, 165,000 ดอลลาร์, 280,000 ดอลลาร์, 220,000 ดอลลาร์, 155,000 ดอลลาร์, 185,000 ดอลลาร์, 160,000 ดอลลาร์, 200,000 ดอลลาร์, 190,000 ดอลลาร์, 140,000 ดอลลาร์, 145.00 ดอลลาร์ 0,…
ราคาบ้านแถว C : 140,000 ดอลลาร์, 130,000 ดอลลาร์, 165,000 ดอลลาร์, 115,000 ดอลลาร์, 170,000 ดอลลาร์, 100,000 ดอลลาร์, 150,000 ดอลลาร์, 180,000 ดอลลาร์, 190,000 ดอลลาร์, 120,000 ดอลลาร์, 110,000 ดอลลาร์, 130,000 ดอลลาร์, 120,00 ดอลลาร์ 0,…
อย่างไรก็ตาม หากพวกเขาทราบราคา เฉลี่ย (เช่น การวัดแนวโน้มส่วนกลาง) ของบ้านในแต่ละละแวกใกล้เคียง พวกเขาก็จะสามารถปรับแต่งการค้นหาได้รวดเร็วยิ่งขึ้น เนื่องจากพวกเขาสามารถระบุได้ง่ายขึ้นว่าย่านใดมีราคาบ้านที่ตรงกับงบประมาณของพวกเขา:
ราคาเฉลี่ย ของ บ้านในย่าน A: 220,000 เหรียญสหรัฐ
ราคาเฉลี่ยของบ้านในย่าน B : 190,000 เหรียญสหรัฐ
ราคาเฉลี่ยของบ้านในย่าน C : 140,000 เหรียญสหรัฐ
เมื่อทราบราคาบ้านโดยเฉลี่ยในแต่ละละแวกใกล้เคียง พวกเขาจะทราบได้อย่างรวดเร็วว่าย่าน C มีแนวโน้มที่จะมีบ้านว่างมากที่สุดภายในงบประมาณของตน
นี่คือประโยชน์ของการใช้การวัดแนวโน้มจากศูนย์กลาง: ช่วยให้คุณเข้าใจค่ากลางของชุดข้อมูล ซึ่งมีแนวโน้มที่จะอธิบายว่าค่าข้อมูลโดยทั่วไปอยู่ที่ใด ในตัวอย่างนี้ ช่วยให้คู่รักหนุ่มสาวเข้าใจราคาโดยทั่วไปของบ้านในแต่ละละแวกบ้าน
ประเด็นสำคัญ: การวัดแนวโน้มจากศูนย์กลางมีประโยชน์เนื่องจากจะให้ค่าเดียวที่อธิบาย “ศูนย์กลาง” ของชุดข้อมูล สิ่งนี้ช่วยให้เราเข้าใจชุดข้อมูลได้เร็วกว่าการดูค่าเดี่ยวทั้งหมดในชุดข้อมูลมาก
หมายถึง
การวัดแนวโน้มส่วนกลางที่ใช้กันมากที่สุดคือ ค่าเฉลี่ย ในการคำนวณค่าเฉลี่ยของชุดข้อมูล เพียงบวกค่าแต่ละค่าทั้งหมดแล้วหารด้วยจำนวนค่าทั้งหมด
ค่าเฉลี่ย = (ผลรวมของค่าทั้งหมด) / (จำนวนค่าทั้งหมด)
ตัวอย่างเช่น สมมติว่าเรามีชุดข้อมูลต่อไปนี้ที่แสดงจำนวนโฮมรันที่ผู้เล่นเบสบอล 10 คนในทีมเดียวกันโจมตีระหว่างฤดูกาล:
| ผู้เล่น | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #สิบ |
|---|---|---|---|---|---|---|---|---|---|---|
| โฮมรัน | 8 | 15 | 22 | 21 | 12 | 9 | 11 | 27 | 14 | 13 |
จำนวนการตีโฮมรันเฉลี่ยต่อผู้เล่นสามารถคำนวณได้ดังนี้:
ค่าเฉลี่ย = (8+15+22+21+12+9+11+27+14+13) / 10 = 15.2 วงจร
ค่ามัธยฐาน
ค่ามัธยฐาน คือค่ากลางของชุดข้อมูล คุณสามารถหาค่ามัธยฐานได้โดยการเรียงลำดับค่าแต่ละค่าทั้งหมดในชุดข้อมูลจากน้อยไปหามากแล้วค้นหาค่ามัธยฐาน หากมีค่าเป็นจำนวนคี่ ค่ามัธยฐานจะเป็นค่าตรงกลาง หากมีค่าเป็นจำนวนคู่ ค่ามัธยฐานคือค่าเฉลี่ยของค่ากลางสองค่า
ตัวอย่างเช่น หากต้องการหาค่ามัธยฐานของจำนวนโฮมรันที่โดนผู้เล่นเบสบอล 10 คนในตัวอย่างก่อนหน้านี้ เราสามารถจัดอันดับผู้เล่นโดยเรียงลำดับจากมากไปน้อยของจำนวนโฮมรันที่โดน:
| ผู้เล่น | #1 | #6 | #7 | #5 | #สิบ | #9 | #2 | #4 | #3 | #8 |
|---|---|---|---|---|---|---|---|---|---|---|
| โฮมรัน | 8 | 9 | 11 | 12 | 13 | 14 | 15 | 21 | 22 | 27 |
เนื่องจากเรามีค่าเป็นจำนวนคู่ ค่ามัธยฐานจึงเป็นเพียงค่าเฉลี่ยของค่ากลางสองค่า: 13.5
ให้พิจารณาว่าเรามีผู้เล่นเก้าคนแทน:
| ผู้เล่น | #1 | #6 | #7 | #5 | #9 | #2 | #4 | #3 | #8 |
|---|---|---|---|---|---|---|---|---|---|
| โฮมรัน | 8 | 9 | 11 | 12 | 14 | 15 | 21 | 22 | 27 |
ในกรณีนี้ เนื่องจากเรามีค่าเป็นจำนวนคี่ ค่ามัธยฐานจึงเป็นเพียงค่าตรงกลาง: 14
แฟชั่น
โหมด คือค่าที่ปรากฏบ่อยที่สุดในชุดข้อมูล ชุดข้อมูลไม่สามารถมีโหมดได้ (หากไม่มีค่าซ้ำ) โหมดเดียวหรือหลายโหมด
ตัวอย่างเช่น ชุดข้อมูลต่อไปนี้ไม่มีโหมด:
| ผู้เล่น | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #สิบ |
|---|---|---|---|---|---|---|---|---|---|---|
| โฮมรัน | 8 | 9 | 11 | 12 | 13 | 14 | 15 | 21 | 22 | 27 |
ชุดข้อมูลต่อไปนี้มีโหมด: 15 นี่คือค่าที่ปรากฏบ่อยที่สุด
| ผู้เล่น | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #สิบ |
|---|---|---|---|---|---|---|---|---|---|---|
| โฮมรัน | 8 | 9 | 11 | 12 | 13 | 15 | 15 | 21 | 22 | 27 |
ชุดข้อมูลต่อไปนี้มีสามโหมด: 8, 15, 19 นี่คือค่าที่ปรากฏบ่อยที่สุด
| ผู้เล่น | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #สิบ |
|---|---|---|---|---|---|---|---|---|---|---|
| โฮมรัน | 8 | 8 | 11 | 12 | 15 | 15 | 17 | 19 | 19 | 27 |
โหมดสามารถเป็นประโยชน์อย่างยิ่งในการวัดแนวโน้มจากศูนย์กลางเมื่อทำงานกับข้อมูลเชิงหมวดหมู่ เนื่องจากโหมดจะบอกเราว่าหมวดหมู่ใดปรากฏบ่อยที่สุด ตัวอย่างเช่น พิจารณาแผนภูมิแท่งต่อไปนี้ซึ่งแสดงผลการสำรวจเกี่ยวกับสีโปรดของผู้คน:
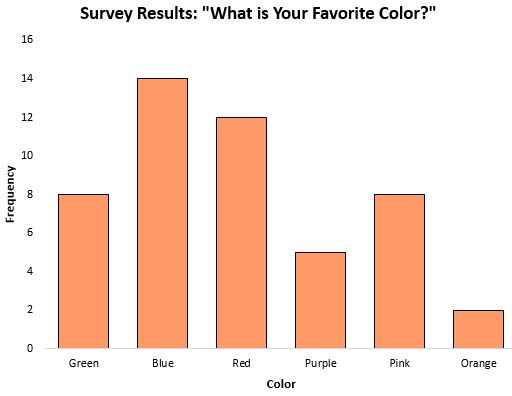
โหมด หรือการตอบสนองที่เกิดขึ้นบ่อยที่สุดเป็นสีน้ำเงิน
ในสถานการณ์ที่ข้อมูลอยู่ในหมวดหมู่ (เช่นข้อมูลข้างต้น) จะไม่สามารถคำนวณค่ามัธยฐานหรือค่าเฉลี่ยได้ ดังนั้นโหมดนี้จึงเป็นการวัดแนวโน้มศูนย์กลางเพียงอย่างเดียวที่เราสามารถใช้ได้
โหมดนี้ยังใช้กับข้อมูลตัวเลขได้ ดังที่เราเห็นในตัวอย่างด้านบนกับผู้เล่นเบสบอล อย่างไรก็ตาม โหมดมีแนวโน้มที่จะมีประโยชน์น้อยกว่าในการตอบคำถาม “ค่าทั่วไปสำหรับชุดข้อมูลนี้คืออะไร” »
ตัวอย่างเช่น สมมติว่าเราต้องการทราบจำนวนโฮมรันโดยทั่วไปที่นักเบสบอลในทีมนี้ตี:
| ผู้เล่น | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #สิบ |
|---|---|---|---|---|---|---|---|---|---|---|
| โฮมรัน | 8 | 8 | 11 | 12 | 15 | 15 | 17 | 19 | 19 | 27 |
โหมดสำหรับชุดข้อมูลนี้คือ 8, 15 และ 19 เนื่องจากเป็นค่าที่พบบ่อยที่สุด อย่างไรก็ตาม สิ่งเหล่านี้ไม่ได้มีประโยชน์มากนักในการทำความเข้าใจจำนวนโฮมรันโดยทั่วไปที่ผู้เล่นในทีมตี การวัดแนวโน้มศูนย์กลางที่ดีกว่าในกรณีนี้คือค่ามัธยฐาน (15) หรือค่าเฉลี่ย (15 เช่นกัน)
โหมดนี้ยังเป็นการวัดแนวโน้มศูนย์กลางที่ไม่ดีนัก เมื่อเป็นตัวเลขที่อยู่ไกลจากค่าที่เหลือ ตัวอย่างเช่น โหมดของชุดข้อมูลต่อไปนี้คือ 30 แต่จริงๆ แล้วไม่ได้แสดงถึงจำนวนโฮมรัน “ทั่วไป” ต่อผู้เล่นในทีม:
| ผู้เล่น | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #สิบ |
|---|---|---|---|---|---|---|---|---|---|---|
| โฮมรัน | 5 | 6 | 7 | สิบ | 11 | 12 | 13 | 15 | 30 | 30 |
ขอย้ำอีกครั้งว่าค่าเฉลี่ยหรือค่ามัธยฐานจะอธิบายตำแหน่งศูนย์กลางของชุดข้อมูลได้ดีกว่า
เมื่อใดควรใช้ค่าเฉลี่ย ค่ามัธยฐาน และโหมด
เราพบว่าค่าเฉลี่ย ค่ามัธยฐาน และโหมดล้วนวัดตำแหน่งศูนย์กลางหรือ “ค่าทั่วไป” ของชุดข้อมูลด้วยวิธีที่แตกต่างกันมาก:
ค่าเฉลี่ย: ค้นหาค่าเฉลี่ยในชุดข้อมูล
ค่ามัธยฐาน: ค้นหาค่ามัธยฐานในชุดข้อมูล
โหมด: ค้นหาค่าที่พบบ่อยที่สุดในชุดข้อมูล
ต่อไปนี้เป็นสถานการณ์ที่มาตรการบางอย่างของแนวโน้มจากส่วนกลางดีกว่าการใช้อื่นๆ:
เมื่อใดจึงควรใช้ค่าเฉลี่ย
วิธีที่ดีที่สุดคือใช้ค่าเฉลี่ยเมื่อการกระจายข้อมูลค่อนข้างสมมาตรและไม่มีค่าผิดปกติ
ตัวอย่างเช่น สมมติว่าเรามีการกระจายต่อไปนี้ซึ่งแสดงเงินเดือนของบุคคลในเมืองหนึ่งๆ:

เนื่องจากการแจกแจงนี้ค่อนข้างสมมาตร (เช่น หากคุณแบ่งครึ่ง แต่ละครึ่งจะดูเท่ากันโดยประมาณ) และไม่มีค่าผิดปกติ (เช่น (บอกว่าไม่มีเงินเดือนสูงมาก) ค่าเฉลี่ยจะทำงานได้ดีในการอธิบายชุดข้อมูลนี้
ค่าเฉลี่ยกลายเป็น 63,000 ดอลลาร์ ซึ่งอยู่ตรงกลางของการแจกแจงโดยประมาณ:

เมื่อใดจึงจะใช้ค่ามัธยฐาน
วิธีที่ดีที่สุดคือใช้ค่ามัธยฐานเมื่อการกระจายข้อมูลบิดเบี้ยวหรือเมื่อมีค่าผิดปกติ
ข้อมูลเอนเอียง:
เมื่อการกระจายตัวเอียง ค่ามัธยฐานยังคงสามารถจับภาพตำแหน่งศูนย์กลางได้ ตัวอย่างเช่น พิจารณาการกระจายเงินเดือนของบุคคลในเมืองใดเมืองหนึ่งดังต่อไปนี้:

ค่ามัธยฐานสะท้อนถึงเงินเดือน “ทั่วไป” ของแต่ละบุคคลได้ดีกว่าค่าเฉลี่ย เนื่องจากค่าขนาดใหญ่ที่ส่วนท้ายของการแจกแจงมีแนวโน้มที่จะย้ายค่าเฉลี่ยออกจากจุดศูนย์กลางไปทางหางยาว
ในตัวอย่างนี้ ค่าเฉลี่ยบอกเราว่าบุคคลทั่วไปมีรายได้ประมาณ $47,000 ต่อปีในเมืองนี้ ในขณะที่ค่ามัธยฐานบอกเราว่าบุคคลทั่วไปมีรายได้เพียงประมาณ $32,000 ต่อปีเท่านั้น ซึ่งเป็นตัวแทนของบุคคลทั่วไปมากกว่ามาก
ค่าผิดปกติ:
ค่ามัธยฐานยังช่วยให้จับตำแหน่งศูนย์กลางของการแจกแจงได้ดีขึ้นเมื่อมีค่าผิดปกติในข้อมูล ตัวอย่างเช่น ลองพิจารณากราฟต่อไปนี้ซึ่งแสดงพื้นที่เป็นตารางฟุตของบ้านบนถนนเส้นหนึ่ง:

ค่าเฉลี่ยได้รับอิทธิพลอย่างมากจากบ้านหลังใหญ่มากบางหลัง ในขณะที่ค่ามัธยฐานไม่ได้รับอิทธิพล ดังนั้นค่ามัธยฐานจึงทำงานได้ดีกว่าในการจับภาพพื้นที่เป็นตารางฟุต “ทั่วไป” ของบ้านบนถนนเส้นนั้นมากกว่าค่าเฉลี่ย
เมื่อใดควรใช้โหมด
โหมดนี้เหมาะที่สุดเมื่อคุณทำงานกับข้อมูลที่เป็นหมวดหมู่ และต้องการทราบว่าหมวดหมู่ใดปรากฏบ่อยที่สุด นี่คือตัวอย่างบางส่วน:
- คุณกำลังทำแบบสำรวจเกี่ยวกับสีโปรดของผู้คน และต้องการทราบว่าสีใดปรากฏบ่อยที่สุดในคำตอบ
- คุณกำลังดำเนินการสำรวจความชอบของผู้คนจากสามตัวเลือกสำหรับการออกแบบเว็บไซต์ และต้องการทราบว่าผู้คนชอบการออกแบบใดมากที่สุด
ตามที่กล่าวไว้ข้างต้น หากคุณกำลังทำงานกับข้อมูลเชิงหมวดหมู่ คุณจะไม่สามารถคำนวณค่ามัธยฐานหรือค่าเฉลี่ยได้ ซึ่งจะทำให้โหมดนี้เป็นเพียงการวัดแนวโน้มจากศูนย์กลางเท่านั้น
โดยทั่วไป หากคุณกำลังทำงานกับข้อมูลตัวเลข เช่น พื้นที่เป็นตารางฟุตของบ้าน จำนวนโฮมรันที่เข้าชมต่อผู้เล่น เงินเดือนต่อบุคคล ฯลฯ โดยปกติแล้ว ควรใช้ค่ามัธยฐานหรือค่าเฉลี่ยเพื่ออธิบายค่า “ทั่วไป” ใน ชุดข้อมูล
หมายเหตุ: สิ่งสำคัญคือต้องทราบว่าหากชุดข้อมูลมีการกระจายตามปกติ อย่างสมบูรณ์ ค่าเฉลี่ย ค่ามัธยฐาน และโหมดทั้งหมดจะมีค่าเท่ากัน