วิธีการพล็อตเส้นโค้ง roc หลายอันใน python (พร้อมตัวอย่าง)

วิธีหนึ่งในการแสดงภาพประสิทธิภาพของ แบบจำลองการจำแนกประเภท ในแมชชีนเลิร์นนิงคือการสร้าง เส้นโค้ง ROC ซึ่งย่อมาจากเส้นโค้ง “ลักษณะการทำงานของตัวรับ”

บ่อยครั้ง คุณอาจต้องการปรับโมเดลการจัดหมวดหมู่หลายรายการให้พอดีกับชุดข้อมูลเดียว และสร้างเส้นโค้ง ROC สำหรับแต่ละโมเดลเพื่อให้เห็นภาพว่าโมเดลใดทำงานได้ดีที่สุดกับข้อมูล

ตัวอย่างทีละขั้นตอนต่อไปนี้แสดงวิธีการพล็อตเส้นโค้ง ROC หลายเส้นใน Python

ขั้นตอนที่ 1: นำเข้าแพ็คเกจที่จำเป็น

ขั้นแรก เราจะนำเข้าแพ็คเกจที่จำเป็นหลายอย่างลงใน Python:

 from sklearn import metrics
from sklearn import datasets
from sklearn. model_selection import train_test_split
from sklearn. linear_model import LogisticRegression
from sklearn. set import GradientBoostingClassifier
import numpy as np
import matplotlib. pyplot as plt

ขั้นตอนที่ 2: สร้างข้อมูลปลอม

ต่อไป เราจะใช้ฟังก์ชัน make_classification() ของ sklearn เพื่อสร้างชุดข้อมูลปลอมที่มี 1,000 แถว ตัวแปรทำนาย 4 ตัว และตัวแปรตอบกลับแบบไบนารี:

 #create fake dataset
X, y = datasets. make_classification (n_samples= 1000 ,
                                    n_features= 4 ,
                                    n_informative= 3 ,
                                    n_redundant= 1 ,
                                    random_state= 0 )

#split dataset into training and testing set
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size= .3 , random_state= 0 )

ขั้นตอนที่ 3: ปรับหลายโมเดลและพล็อต ROC Curves

ต่อไป เราจะใส่โมเดลการถดถอยโลจิสติก จากนั้นจึงใส่โมเดลที่มีการไล่ระดับสีเข้ากับข้อมูลและลงจุดเส้นโค้ง ROC สำหรับแต่ละรุ่นบนพล็อตเดียวกัน:

 #set up plotting area
plt. Figure (0). clf ()

#fit logistic regression model and plot ROC curve
model = LogisticRegression()
model. fit (X_train, y_train)
y_pred = model. predict_proba (X_test)[:, 1]
fpr, tpr, _ = metrics. roc_curve (y_test, y_pred)
auc = round(metrics. roc_auc_score (y_test, y_pred), 4)
plt. plot (fpr,tpr,label="Logistic Regression, AUC="+str(auc))

#fit gradient boosted model and plot ROC curve
model = GradientBoostingClassifier()
model. fit (X_train, y_train)
y_pred = model. predict_proba (X_test)[:, 1]
fpr, tpr, _ = metrics. roc_curve (y_test, y_pred)
auc = round(metrics. roc_auc_score (y_test, y_pred), 4)
plt. plot (fpr,tpr,label="Gradient Boosting, AUC="+str(auc))

#add legend
plt. legend () 

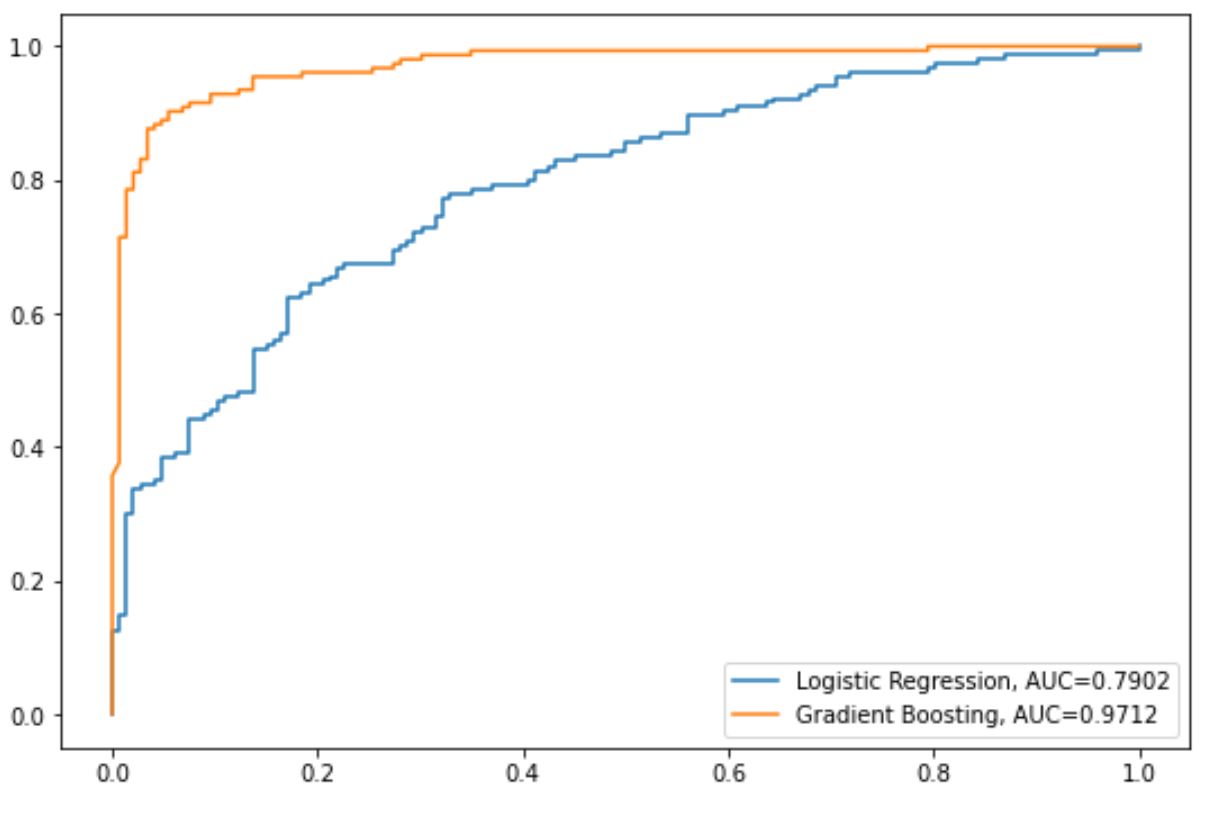
เส้นสีน้ำเงินแสดงเส้นโค้ง ROC สำหรับแบบจำลองการถดถอยโลจิสติก และเส้นสีส้มแสดงเส้นโค้ง ROC สำหรับแบบจำลองที่เน้นการไล่ระดับสี

ยิ่งเส้นโค้ง ROC พอดีกับมุมซ้ายบนของพล็อตมากเท่าไร โมเดลก็ยิ่งสามารถจำแนกข้อมูลเป็นหมวดหมู่ได้ดีขึ้นเท่านั้น

ในการหาปริมาณ เราสามารถคำนวณ AUC ซึ่งเป็นพื้นที่ใต้เส้นโค้ง ซึ่งจะบอกเราว่าพล็อตอยู่ใต้เส้นโค้งเป็นจำนวนเท่าใด

ยิ่ง AUC ใกล้ 1 มากเท่าใด โมเดลก็ยิ่งดีเท่านั้น

จากแผนภูมิของเรา เราจะเห็นเมตริก AUC ต่อไปนี้สำหรับแต่ละรุ่น:

• AUC ของแบบจำลองการถดถอยโลจิสติก: 0.7902
• AUC ของแบบจำลองที่เสริมด้วยเกรเดียนต์: 0.9712

แน่นอนว่าแบบจำลองที่ปรับปรุงการไล่ระดับสีจะประสบความสำเร็จในการจำแนกข้อมูลเป็นหมวดหมู่มากกว่าแบบจำลองการถดถอยโลจิสติก

แหล่งข้อมูลเพิ่มเติม

บทช่วยสอนต่อไปนี้ให้ข้อมูลเพิ่มเติมเกี่ยวกับแบบจำลองการจำแนกประเภทและเส้นโค้ง ROC:

รู้เบื้องต้นเกี่ยวกับการถดถอยโลจิสติก
วิธีการตีความ ROC Curve (พร้อมตัวอย่าง)
คะแนน AUC ที่ดีคืออะไร?