วิธีการดำเนินการวิเคราะห์ความแปรปรวนแบบทางเดียวใน excel

การวิเคราะห์ ความแปรปรวนแบบทางเดียว (“การวิเคราะห์ความแปรปรวน”) ใช้เพื่อพิจารณาว่ามีความแตกต่างที่มีนัยสำคัญทางสถิติระหว่างค่าเฉลี่ยของกลุ่มอิสระสามกลุ่มขึ้นไปหรือไม่

บทช่วยสอนนี้จะอธิบายวิธีการดำเนินการวิเคราะห์ความแปรปรวนแบบทางเดียวใน Excel

ตัวอย่าง: การวิเคราะห์ความแปรปรวนแบบทางเดียวใน Excel

สมมติว่านักวิจัยรับสมัครนักศึกษาจำนวน 30 คนเพื่อเข้าร่วมการศึกษาวิจัย นักเรียนจะได้รับการสุ่มให้ใช้หนึ่งในสามเทคนิคการเรียนในช่วงสามสัปดาห์ข้างหน้าเพื่อเตรียมตัวสอบ เมื่อสิ้นสุดสามสัปดาห์ นักเรียนทุกคนจะทำแบบทดสอบเดียวกัน

ผลการทดสอบของนักเรียนแสดงไว้ด้านล่าง:

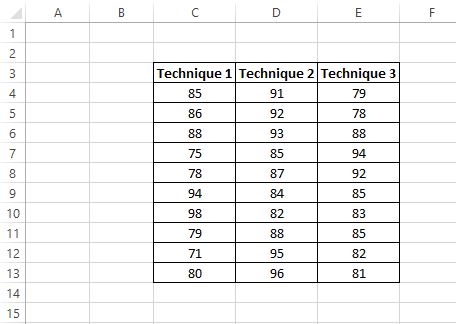
ผู้วิจัยต้องการทำการวิเคราะห์ความแปรปรวนแบบทางเดียวเพื่อตรวจสอบว่าคะแนนเฉลี่ยของทั้ง 3 กลุ่มเท่ากันหรือไม่

เมื่อต้องการดำเนินการวิเคราะห์ความแปรปรวนแบบทางเดียวใน Excel ให้ไปที่แท็บ ข้อมูล จากนั้นคลิกตัวเลือก การวิเคราะห์ข้อมูล ในกลุ่ม การวิเคราะห์

หากคุณไม่เห็นตัวเลือก การวิเคราะห์ข้อมูล คุณ ต้อง โหลดซอฟต์แวร์ Analysis ToolPak ฟรีก่อน

เมื่อคุณคลิก หน้าต่างจะปรากฏขึ้นพร้อมตัวเลือกเครื่องมือสแกนต่างๆ เลือก Anova: Single Factor แล้วคลิก ตกลง

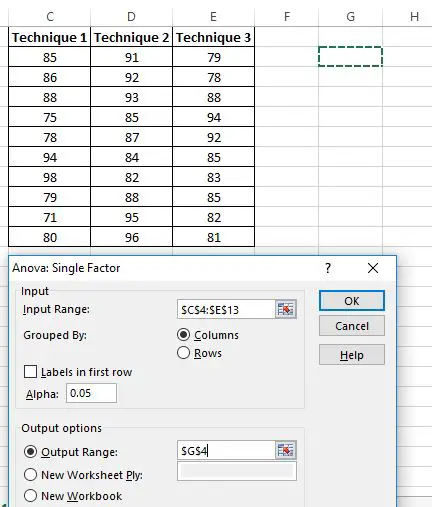
หน้าต่างใหม่จะปรากฏขึ้นเพื่อขอ ช่วงอินพุต คุณสามารถลากกล่องรอบๆ ข้อมูลของคุณหรือป้อนช่วงข้อมูลด้วยตนเองก็ได้ ในกรณีนี้ ข้อมูลของเราอยู่ในเซลล์ C4:E13

จากนั้นเลือกระดับ อัลฟ่า สำหรับการทดสอบ โดยค่าเริ่มต้น ตัวเลขนี้คือ 0.05 ในกรณีนี้ ผมจะปล่อยไว้ที่ 0.05

สุดท้าย ให้เลือกเซลล์สำหรับ Output Range ซึ่งผลลัพธ์ ANOVA แบบทางเดียวจะปรากฏขึ้น ในกรณีนี้ ฉันเลือกเซลล์ G4

เมื่อคุณคลิก ตกลง ผลลัพธ์ ANOVA แบบทางเดียวจะปรากฏขึ้น:

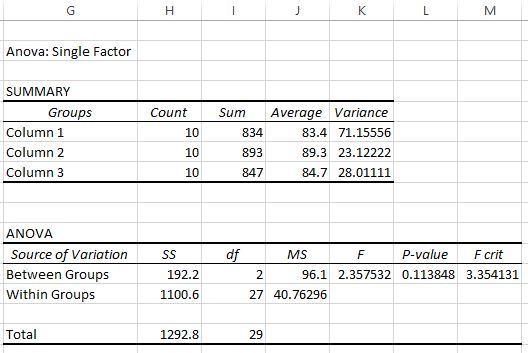
การตีความผลลัพธ์

ตารางสองตารางจะแสดงอยู่ในเอาต์พุต ตารางแรกเป็นตารางสรุปที่แสดงจำนวนคะแนนสอบในแต่ละกลุ่ม ผลรวมของคะแนนสอบ ค่าเฉลี่ยของคะแนนสอบ และความแปรปรวนของคะแนนสอบ

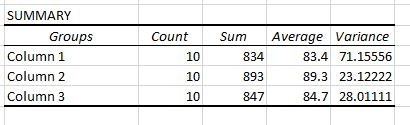
โปรดจำไว้ว่าการวิเคราะห์ความแปรปรวนแบบทางเดียวใช้เพื่อพิจารณาว่ามีความแตกต่างที่มีนัยสำคัญทางสถิติระหว่างค่าเฉลี่ยของกลุ่มสามกลุ่มขึ้นไปหรือไม่

จากตารางแรกนี้ เราจะเห็นว่าคะแนนเฉลี่ยของแต่ละกลุ่มมีความแตกต่างกัน แต่หากต้องการทราบว่าความแตกต่างเหล่านี้มีนัยสำคัญทางสถิติหรือไม่ เราจำเป็นต้องดูตารางที่สอง

ตารางที่สองแสดงสถิติการทดสอบ F ค่า F วิกฤต และค่า p:

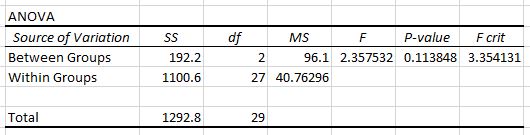
ในกรณีนี้ สถิติการทดสอบ F คือ 2.3575 และ ค่าวิกฤตของ F คือ 3.3541 เนื่องจากสถิติการทดสอบ F น้อยกว่าค่าวิกฤตของ F เราจึงไม่มีหลักฐานเพียงพอที่จะปฏิเสธสมมติฐานว่างที่ว่าค่าเฉลี่ยของทั้งสามกลุ่มเท่ากัน

ซึ่งหมายความว่าเราไม่มีหลักฐานเพียงพอที่จะบอกว่ามีผลการทดสอบระหว่างเทคนิคการศึกษาทั้งสามนี้แตกต่างกัน

เรายังใช้ ค่า p เพื่อหาข้อสรุปเดียวกันได้ ในกรณีนี้ ค่า p คือ 0.1138 ซึ่งสูงกว่าระดับอัลฟ่าที่ 0.05

ซึ่งหมายความว่าเราไม่มีหลักฐานเพียงพอที่จะปฏิเสธสมมติฐานว่างที่ว่าค่าเฉลี่ยของทั้งสามกลุ่มเท่ากัน

หมายเหตุ: ในกรณีที่คุณปฏิเสธสมมติฐานว่าง คุณสามารถทำการ ทดสอบหลังการทดสอบของ Tukey-Kramer เพื่อระบุได้อย่างชัดเจนว่าค่าเฉลี่ยของกลุ่มใดที่แตกต่างกัน