วิธีอ่านเมทริกซ์ความแปรปรวนร่วม

ความแปรปรวนร่วม คือการวัดว่าการเปลี่ยนแปลงในตัวแปรหนึ่งสัมพันธ์กับการเปลี่ยนแปลงในตัวแปรตัวที่สองอย่างไร โดยเฉพาะอย่างยิ่ง มันคือการวัดระดับที่ตัวแปรสองตัวมีความสัมพันธ์กันเชิงเส้นตรง

เมทริกซ์ความแปรปรวนร่วม คือเมทริกซ์จตุรัสที่แสดงความแปรปรวนร่วมระหว่างตัวแปรต่างๆ มากมาย นี่อาจเป็นวิธีที่มีประโยชน์ในการทำความเข้าใจว่าตัวแปรต่างๆ เกี่ยวข้องกันอย่างไรในชุดข้อมูล

ตัวอย่างต่อไปนี้แสดงวิธีการอ่านเมทริกซ์ความแปรปรวนร่วมในทางปฏิบัติ

วิธีอ่านเมทริกซ์ความแปรปรวนร่วม

สมมติว่าเรามีเมทริกซ์ความแปรปรวนร่วมต่อไปนี้ซึ่งมีข้อมูลเกี่ยวกับคะแนนสอบสำหรับวิชาที่แตกต่างกันสามวิชาสำหรับนักเรียน:

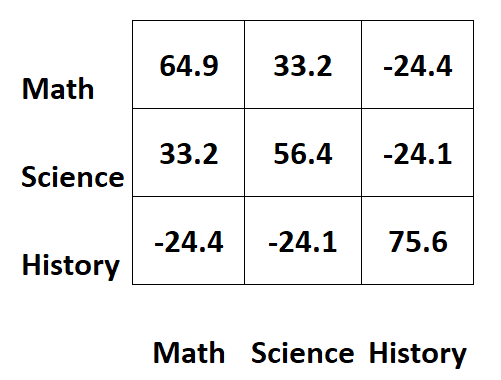
ค่าตามเส้นทแยงมุมของเมทริกซ์แสดงถึงความแปรปรวนของแต่ละเรื่อง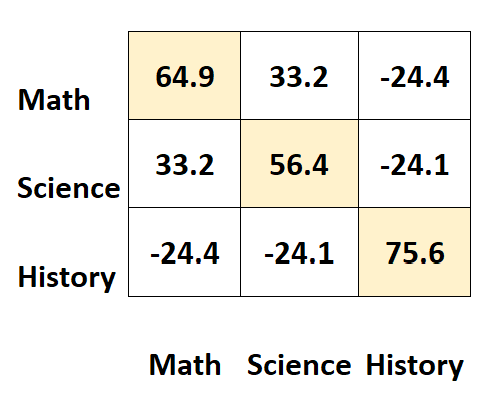

ตัวอย่างเช่น:

• ความแปรปรวนของผลลัพธ์ทางคณิตศาสตร์คือ 64.9
• ความแปรปรวนของคะแนนวิทยาศาสตร์คือ 56.4
• ความแปรปรวนของคะแนนในอดีตคือ 75.6

ค่าอื่นๆ ของเมทริกซ์แสดงถึงความแปรปรวนร่วมระหว่างวิชาต่างๆ

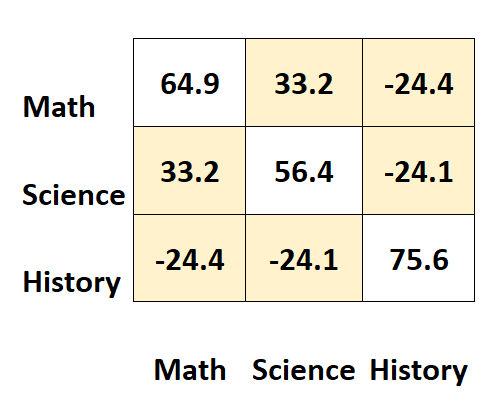
ตัวอย่างเช่น:

• ความแปรปรวนร่วมระหว่างคะแนนคณิตศาสตร์และวิทยาศาสตร์คือ 33.2
• ความแปรปรวนร่วมระหว่างคะแนนคณิตศาสตร์และประวัติศาสตร์คือ –24.4
• ความแปรปรวนร่วมระหว่างคะแนนวิทยาศาสตร์และประวัติศาสตร์คือ –24.1

จำนวนบวก สำหรับความแปรปรวนร่วมบ่งชี้ว่าตัวแปรสองตัวมีแนวโน้มเพิ่มขึ้นหรือลดลงตามกัน

ตัวอย่างเช่น คณิตศาสตร์และวิทยาศาสตร์มีความแปรปรวนร่วมเชิงบวก ( 33.2 ) ซึ่งบ่งชี้ว่านักเรียนที่ได้คะแนนสูงในวิชาคณิตศาสตร์ก็มีแนวโน้มที่จะได้คะแนนสูงในวิชาวิทยาศาสตร์เช่นกัน

ในทางกลับกัน นักเรียนที่มีผลการเรียนไม่ดีในวิชาคณิตศาสตร์ก็มักจะมีผลการเรียนไม่ดีในวิชาวิทยาศาสตร์เช่นกัน

จำนวนลบ สำหรับความแปรปรวนร่วมบ่งชี้ว่าเมื่อตัวแปรตัวหนึ่งเพิ่มขึ้น ตัวแปรตัวที่สองมีแนวโน้มลดลง

ตัวอย่างเช่น คณิตศาสตร์และประวัติศาสตร์มีความแปรปรวนร่วมเป็นลบ ( -24.44 ) ซึ่งบ่งชี้ว่านักเรียนที่มีผลการเรียนคณิตศาสตร์สูงมักจะมีผลการเรียนต่ำในประวัติศาสตร์

ในทางกลับกัน นักเรียนที่ได้คะแนนคณิตศาสตร์ต่ำมักจะได้คะแนนสูงในประวัติศาสตร์

หมายเหตุเกี่ยวกับความสมมาตรของเมทริกซ์ความแปรปรวนร่วม

ควรสังเกตว่าเมทริกซ์ความแปรปรวนร่วมมีความสมมาตรอย่างสมบูรณ์แบบ

ตัวอย่างเช่น เซลล์ด้านบนขวาจะแสดงค่าเดียวกันกับเซลล์ด้านล่างซ้ายทุกประการ:

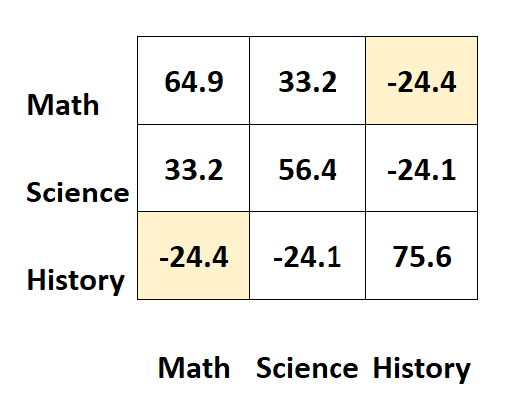
แท้จริงแล้วทั้งสองเซลล์วัดความแปรปรวนร่วมระหว่างประวัติศาสตร์และคณิตศาสตร์

เนื่องจากเมทริกซ์ความแปรปรวนร่วมมีความสมมาตร ค่าครึ่งหนึ่งของค่าความแปรปรวนร่วมที่แสดงในเมทริกซ์จึงซ้ำซ้อนและไม่จำเป็น

ดังนั้น บางครั้งจะแสดงเพียงครึ่งหนึ่งของเมทริกซ์ความแปรปรวนร่วมเท่านั้น:

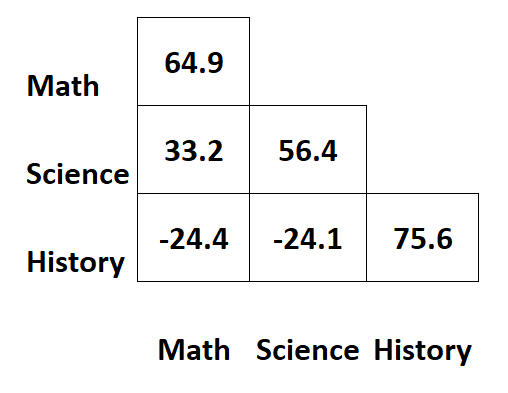
เมื่อใดจึงควรใช้เมทริกซ์ความแปรปรวนร่วม

ในทางปฏิบัติ คุณมักจะต้องสร้างและตีความ เมทริกซ์สหสัมพันธ์ บ่อยกว่าเมทริกซ์ความแปรปรวนร่วม

อย่างไรก็ตาม เมทริกซ์ความแปรปรวนร่วมมักถูกใช้ “เบื้องหลัง” สำหรับอัลกอริธึมและโมเดลการเรียนรู้ของเครื่องที่แตกต่างกัน

ตัวอย่างเช่น เมทริกซ์ความแปรปรวนร่วมถูกใช้ในระหว่าง การวิเคราะห์องค์ประกอบหลัก ซึ่งช่วยให้เราเข้าใจรูปแบบที่ซ่อนอยู่ในชุดข้อมูลที่มีตัวแปรจำนวนมาก

แหล่งข้อมูลเพิ่มเติม

บทช่วยสอนต่อไปนี้จะอธิบายวิธีสร้างเมทริกซ์ความแปรปรวนร่วมโดยใช้ซอฟต์แวร์ทางสถิติต่างๆ

วิธีสร้างเมทริกซ์ความแปรปรวนร่วมใน R
วิธีสร้างเมทริกซ์ความแปรปรวนร่วมใน Python
วิธีสร้างเมทริกซ์ความแปรปรวนร่วมใน SPSS
วิธีสร้างเมทริกซ์ความแปรปรวนร่วมใน Excel