วิธีดำเนินการถดถอยเชิงเส้นอย่างง่ายใน stata

การถดถอยเชิงเส้นอย่างง่าย เป็นวิธีการที่คุณสามารถใช้เพื่อทำความเข้าใจความสัมพันธ์ระหว่างตัวแปรอธิบาย x และตัวแปรตอบสนอง y

บทช่วยสอนนี้จะอธิบายวิธีการถดถอยเชิงเส้นอย่างง่ายใน Stata

ตัวอย่าง: การถดถอยเชิงเส้นอย่างง่ายใน Stata

สมมติว่าเราต้องการเข้าใจความสัมพันธ์ระหว่างน้ำหนักรถยนต์กับไมล์ต่อแกลลอน ในการสำรวจความสัมพันธ์นี้ เราสามารถทำการถดถอยเชิงเส้นอย่างง่ายโดยใช้น้ำหนักเป็นตัวแปรอธิบาย และใช้ไมล์ต่อแกลลอนเป็นตัวแปรตอบสนอง

ทำตามขั้นตอนต่อไปนี้ใน Stata เพื่อทำการถดถอยเชิงเส้นอย่างง่ายโดยใช้ชุดข้อมูลที่เรียกว่า auto ซึ่งมีข้อมูลของรถยนต์ 74 คันที่แตกต่างกัน

ขั้นตอนที่ 1: โหลดข้อมูล

โหลดข้อมูลโดยพิมพ์ข้อความต่อไปนี้ในกล่องคำสั่ง:

ใช้ https://www.stata-press.com/data/r13/auto

ขั้นตอนที่ 2: รับข้อมูลสรุป

ทำความเข้าใจข้อมูลที่คุณกำลังทำงานอย่างรวดเร็วโดยพิมพ์ข้อความต่อไปนี้ในกล่องคำสั่ง:

เพื่อสรุป

เราจะเห็นได้ว่าชุดข้อมูลมีตัวแปรที่แตกต่างกัน 12 ตัว แต่มีเพียงสองตัวที่เราสนใจคือ mpg และ Weight

ขั้นตอนที่ 3: แสดงภาพข้อมูล

ก่อนที่จะทำการถดถอยเชิงเส้นอย่างง่าย เรามาสร้างแผนภูมิกระจายของน้ำหนักเทียบกับ mpg ก่อน เพื่อให้เราเห็นภาพความสัมพันธ์ระหว่างตัวแปรทั้งสองนี้ และตรวจสอบค่าผิดปกติที่ชัดเจน พิมพ์ข้อความต่อไปนี้ในกล่องคำสั่งเพื่อสร้าง Scatterplot:

การกระจายน้ำหนัก MPG

สิ่งนี้จะสร้างพล็อตกระจายต่อไปนี้:

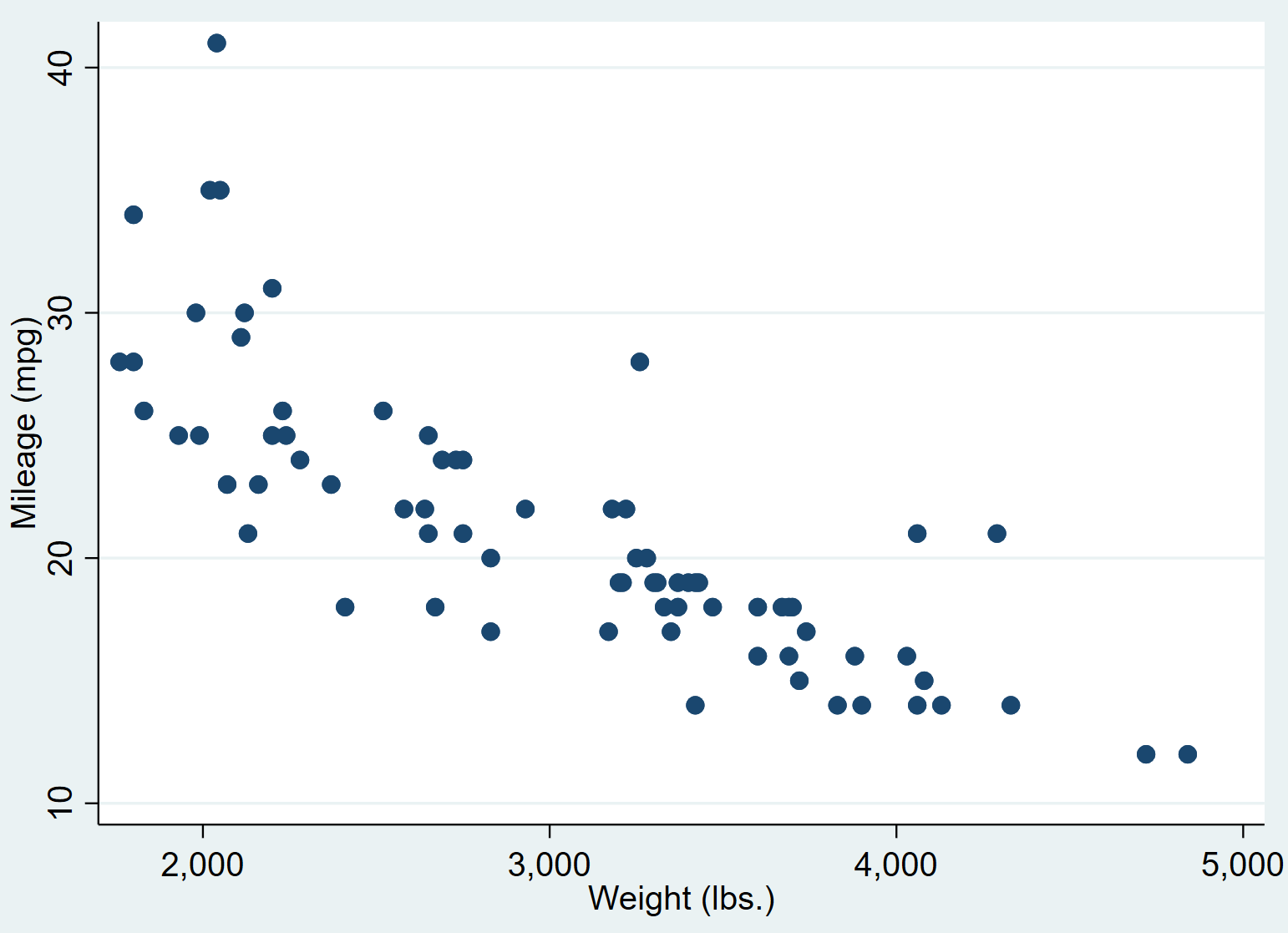
เราจะเห็นได้ว่ารถยนต์ที่มีน้ำหนักมากกว่ามักจะใช้ไมล์ต่อแกลลอนน้อยกว่า ในการหาปริมาณความสัมพันธ์นี้ เราจะทำการถดถอยเชิงเส้นอย่างง่าย

ขั้นตอนที่ 4: ทำการถดถอยเชิงเส้นอย่างง่าย

พิมพ์ข้อความต่อไปนี้ในกล่องคำสั่งเพื่อดำเนินการถดถอยเชิงเส้นอย่างง่ายโดยใช้น้ำหนักเป็นตัวแปรอธิบายและ mpg เป็นตัวแปรตอบสนอง

น้ำหนักถดถอยเป็น mpg

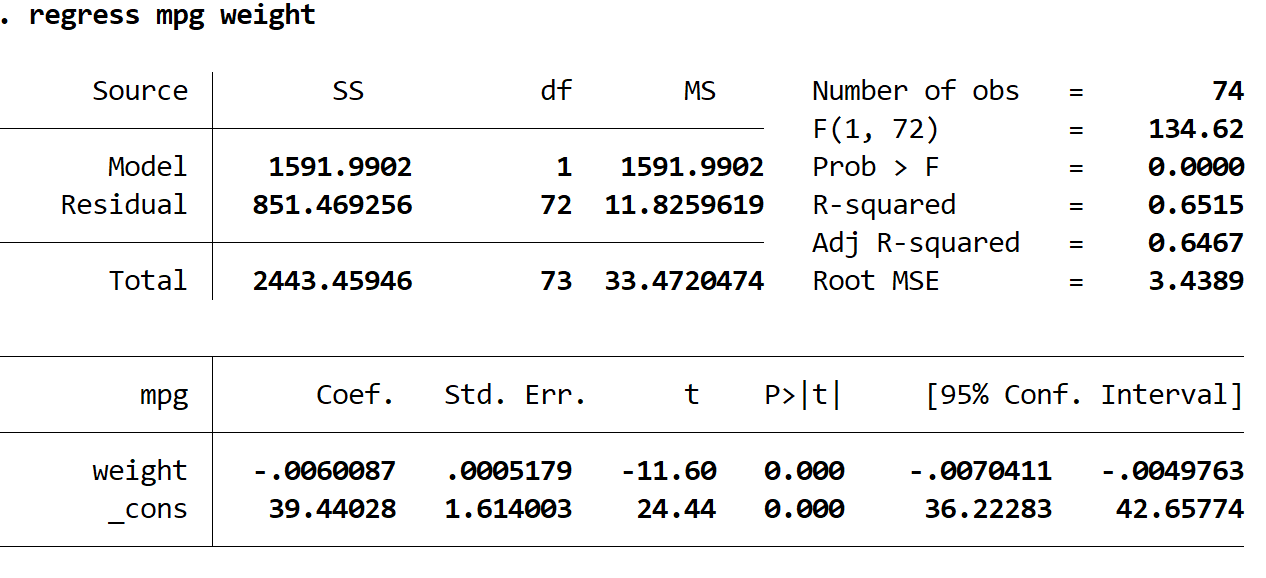
วิธีการตีความตัวเลขที่น่าสนใจที่สุดในผลลัพธ์มีดังนี้:

R กำลังสอง: 0.6515 นี่คือสัดส่วนของความแปรปรวนในตัวแปรตอบสนองที่สามารถอธิบายได้ด้วยตัวแปรอธิบาย ในตัวอย่างนี้ 65.15% ของการเปลี่ยนแปลงใน mpg สามารถอธิบายได้ด้วยน้ำหนัก

ค่า Coef (น้ำหนัก): -0.006 สิ่งนี้บอกเราถึงการเปลี่ยนแปลงโดยเฉลี่ยในตัวแปรตอบสนองที่เกี่ยวข้องกับการเพิ่มขึ้นของตัวแปรอธิบายหนึ่งหน่วย ในตัวอย่างนี้ น้ำหนักที่เพิ่มขึ้นทุกๆ 1 ปอนด์สัมพันธ์กับการลดลงโดยเฉลี่ย 0.006 mpg

โคฟ (_cons): 39.44028. สิ่งนี้บอกเราถึงค่าเฉลี่ยของตัวแปรตอบสนองเมื่อตัวแปรอธิบายเป็นศูนย์ ในตัวอย่างนี้ mpg เฉลี่ยคือ 39.44028 เมื่อน้ำหนักของรถเป็นศูนย์ นี่ไม่สมเหตุสมผลเลยที่จะตีความเนื่องจากน้ำหนักของรถไม่สามารถเป็นศูนย์ได้ แต่จำนวน 39.44028 จำเป็นต่อการสร้างสมการถดถอย

ป>|t| (น้ำหนัก): 0.000. นี่คือค่า p ที่เกี่ยวข้องกับสถิติการทดสอบน้ำหนัก ในกรณีนี้ เนื่องจากค่านี้น้อยกว่า 0.05 เราจึงสามารถสรุปได้ว่ามีความสัมพันธ์ที่มีนัยสำคัญทางสถิติระหว่างน้ำหนักและ mpg

สมการการถดถอย: สุดท้ายนี้ เราสามารถสร้างสมการถดถอยโดยใช้ค่าสัมประสิทธิ์ทั้งสองค่าได้ ในกรณีนี้ สมการจะเป็นดังนี้:

MPG ที่คาดการณ์ไว้ = 39.44028 – 0.0060087*(น้ำหนัก)

เราสามารถใช้สมการนี้เพื่อค้นหา MPG ที่คาดหวังสำหรับรถยนต์ โดยพิจารณาจากน้ำหนักของรถ ตัวอย่างเช่น รถยนต์ที่มีน้ำหนัก 4,000 ปอนด์ ควรมีอัตรา MPG อยู่ที่ 15,405:

MPG ที่คาดการณ์ไว้ = 39.44028 – 0.0060087*(4000) = 15.405

ขั้นตอนที่ 5: รายงานผลลัพธ์

สุดท้ายนี้ เราต้องการรายงานผลลัพธ์ของการถดถอยเชิงเส้นอย่างง่ายของเรา นี่คือตัวอย่างของวิธีการทำเช่นนี้:

มีการถดถอยเชิงเส้นเพื่อหาความสัมพันธ์ระหว่างน้ำหนักของรถยนต์กับไมล์ต่อแกลลอน ใช้ตัวอย่างรถยนต์จำนวน 74 คันในการวิเคราะห์

ผลลัพธ์แสดงให้เห็นว่ามีความสัมพันธ์ที่มีนัยสำคัญทางสถิติระหว่างน้ำหนักกับ mpg (t = -11.60, p < 0.0001) และน้ำหนักนั้นคิดเป็น 65.15% ของความแปรปรวนที่อธิบายไว้ใน mpg

สมการถดถอยกลายเป็น:

คาดการณ์ MPG = 39.44 – 0.006 (น้ำหนัก)

แต่ละปอนด์ที่เพิ่มขึ้นสัมพันธ์กับการลดลงโดยเฉลี่ย -0.006 ไมล์ต่อแกลลอน