วิธีตรวจสอบสมมติฐาน anova

การวิเคราะห์ความแปรปรวนแบบทางเดียว คือการทดสอบทางสถิติที่ใช้ในการพิจารณาว่ามีความแตกต่างที่มีนัยสำคัญระหว่างค่าเฉลี่ยของกลุ่มอิสระสามกลุ่มขึ้นไปหรือไม่

นี่คือตัวอย่างของเวลาที่เราอาจใช้การวิเคราะห์ความแปรปรวนแบบทางเดียว:

คุณสุ่มแบ่งชั้นเรียนที่มีนักเรียน 90 คนออกเป็นสามกลุ่ม กลุ่มละ 30 คน แต่ละกลุ่มใช้เทคนิคการเรียนที่แตกต่างกันเป็นเวลาหนึ่งเดือนเพื่อเตรียมตัวสอบ สิ้นเดือนนักเรียนทุกคนจะสอบเหมือนกัน

อยากรู้ว่าเทคนิคการเรียนมีผลต่อคะแนนสอบหรือไม่ ดังนั้น คุณจึงทำการวิเคราะห์ ความแปรปรวนแบบทางเดียว เพื่อดูว่ามีความแตกต่างที่มีนัยสำคัญทางสถิติระหว่างคะแนนเฉลี่ยของทั้งสามกลุ่มหรือไม่

ก่อนที่เราจะดำเนินการวิเคราะห์ความแปรปรวนแบบทางเดียวได้ เราต้องตรวจสอบก่อนว่าเป็นไปตามสมมติฐานสามข้อก่อน

1. ความปกติ – แต่ละตัวอย่างดึงมาจากประชากรที่แจกแจงตามปกติ

2. ความแปรปรวนที่เท่ากัน – ความแปรปรวนของประชากรที่ใช้สุ่มตัวอย่างเท่ากัน

3. ความเป็นอิสระ – การสังเกตภายในแต่ละกลุ่มมีความเป็นอิสระจากกันและการสังเกตภายในกลุ่ม ได้โดยการสุ่มตัวอย่าง

หากไม่เป็นไปตามสมมติฐานเหล่านี้ ผลลัพธ์ของการวิเคราะห์ความแปรปรวนแบบทางเดียวของเราอาจไม่น่าเชื่อถือ

ในบทความนี้ เราจะอธิบายวิธีตรวจสอบสมมติฐานเหล่านี้ และต้องทำอย่างไรหากมีการละเมิดข้อใดข้อหนึ่ง

สมมติฐานที่ 1: ความปกติ

ANOVA ถือว่าแต่ละตัวอย่างมาจากประชากรที่แจกแจงตามปกติ

วิธีตรวจสอบสมมติฐานนี้ใน R:

เพื่อยืนยันสมมติฐานนี้ เราสามารถใช้สองวิธี:

• ตรวจสอบสมมติฐานด้วยสายตาโดยใช้ฮิสโตแกรมหรือ พล็อต QQ
• ตรวจสอบสมมติฐานโดยใช้การทดสอบทางสถิติอย่างเป็นทางการ เช่น Shapiro-Wilk, Kolmogorov-Smironov, Jarque-Barre หรือ D’Agostino-Pearson

ตัวอย่างเช่น สมมติว่าเรารับสมัครคน 90 คนเพื่อเข้าร่วมในการทดลองลดน้ำหนัก โดยเราสุ่มให้คน 30 คนติดตามโปรแกรม A โปรแกรม B หรือโปรแกรม C เป็นเวลาหนึ่งเดือน หากต้องการดูว่าโปรแกรมมีผลกระทบต่อการลดน้ำหนักหรือไม่ เราต้องการทำการวิเคราะห์ความแปรปรวนแบบทางเดียว รหัสต่อไปนี้สาธิตวิธีการตรวจสอบสมมติฐานภาวะปกติโดยใช้ฮิสโตแกรม พล็อต QQ และการทดสอบชาปิโร-วิลค์

1. ติดตั้งโมเดล ANOVA

 #make this example reproducible
set.seed(0)

#create data frame
data <- data. frame (program = rep(c(" A ", " B ", " C "), each = 30 ),
                   weight_loss = c(runif(30, 0, 3),
                                   runif(30, 0, 5),
                                   runif(30, 1, 7)))

#fit the one-way ANOVA model
model <- aov(weight_loss ~ program, data = data)

2. สร้างฮิสโตแกรมของค่าการตอบสนอง

 #create histogram
hist(data$weight_loss)

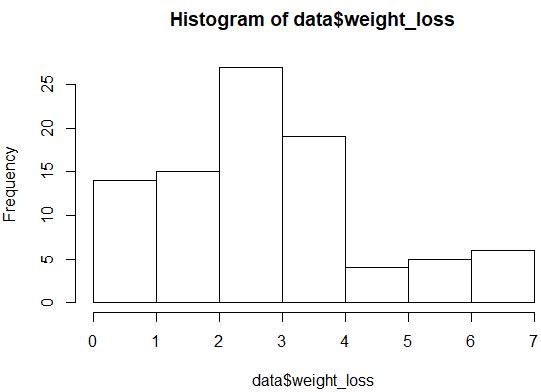
การแจกแจงดูไม่กระจายแบบปกติมากนัก (เช่น ไม่ใช่รูประฆัง) แต่เรายังสามารถสร้างพล็อต QQ เพื่อดูการแจกแจงอีกครั้งได้

3. สร้างแผนผัง QQ ของปริมาณคงเหลือ

 #create QQ plot to compare this dataset to a theoretical normal distribution
qqnorm(model$residuals)

#add straight diagonal line to plot
qqline(model$residuals) 

โดยทั่วไป หากจุดข้อมูลอยู่ตามแนวเส้นทแยงมุมตรงในพล็อต QQ ชุดข้อมูลก็น่าจะเป็นไปตามการแจกแจงแบบปกติ ในกรณีนี้เราจะเห็นได้ว่ามีการเบี่ยงเบนจากเส้นตรงปลายอย่างเห็นได้ชัด ซึ่งอาจบ่งชี้ได้ว่าข้อมูลไม่ได้กระจายตามปกติ

4. ทำการทดสอบ Shapiro-Wilk เพื่อความปกติ

 #Conduct Shapiro-Wilk Test for normality
shapiro. test (data$weight_loss)

#Shapiro-Wilk normality test
#
#data: data$weight_loss
#W = 0.9587, p-value = 0.005999

การทดสอบชาปิโร-วิลค์จะทดสอบสมมติฐานว่างว่าตัวอย่างมาจากการแจกแจงแบบปกติเทียบกับสมมติฐานทางเลือกที่ว่าตัวอย่างไม่ได้มาจากการแจกแจงแบบปกติ ในกรณีนี้ ค่า p ของการทดสอบคือ 0.005999 ซึ่งต่ำกว่าระดับอัลฟ่าที่ 0.05 นี่แสดงให้เห็นว่าตัวอย่างไม่เป็นไปตามการแจกแจงแบบปกติ

จะทำอย่างไรถ้าสมมติฐานนี้ไม่ได้รับการเคารพ:

โดยทั่วไป การวิเคราะห์ความแปรปรวนแบบทางเดียวถือว่าค่อนข้างแข็งแกร่งต่อการละเมิดสมมติฐานภาวะปกติตราบใดที่ขนาดของกลุ่มตัวอย่างมีขนาดใหญ่เพียงพอ

นอกจากนี้ หากคุณมีตัวอย่างจำนวนมาก การทดสอบทางสถิติ เช่น การทดสอบ Shapiro-Wilk มักจะบอกคุณเสมอว่าข้อมูลของคุณไม่ปกติ ด้วยเหตุนี้ จึงมักจะดีที่สุดที่จะตรวจสอบข้อมูลของคุณด้วยภาพโดยใช้แผนภูมิ เช่น ฮิสโตแกรมและแผนภูมิ QQ เพียงแค่ดูกราฟ คุณก็สามารถเข้าใจได้ว่าข้อมูลมีการกระจายตามปกติหรือไม่

หากสมมติฐานเรื่องความเป็นปกติถูกละเมิด อย่างรุนแรง หรือคุณแค่อยากจะอนุรักษ์นิยม คุณมีสองทางเลือก:

(1) แปลงค่าการตอบสนองของข้อมูลของคุณเพื่อให้การแจกแจงมีการกระจายตามปกติมากขึ้น

(2) ทำการทดสอบแบบไม่มีพารามิเตอร์ที่เทียบเท่ากัน เช่น การทดสอบครัสคัล-วาลลิส ซึ่งไม่จำเป็นต้องสันนิษฐานว่าเป็นภาวะปกติ

สมมติฐาน #2: ความแปรปรวนเท่ากัน

ANOVA จะถือว่าความแปรปรวนของประชากรที่ใช้สุ่มตัวอย่างมีค่าเท่ากัน

วิธีตรวจสอบสมมติฐานนี้ใน R:

เราสามารถตรวจสอบสมมติฐานนี้ใน R ได้โดยใช้สองวิธี:

• ตรวจสอบสมมติฐานด้วยสายตาโดยใช้ boxplots
• ทดสอบสมมติฐานโดยใช้การทดสอบทางสถิติอย่างเป็นทางการ เช่น การทดสอบของ Bartlett

รหัสต่อไปนี้สาธิตวิธีการทำเช่นนี้ โดยใช้ชุดข้อมูลการลดน้ำหนักปลอมชุดเดียวกับที่เราสร้างไว้ก่อนหน้านี้

1. สร้างแปลงกล่อง

 #Create box plots that show distribution of weight loss for each group
boxplot(weight_loss ~ program, xlab=' Program ', ylab=' Weight Loss ', data=data)

ความแปรปรวนของการลดน้ำหนักในแต่ละกลุ่มสามารถสังเกตได้จากความยาวของแต่ละบ็อกซ์พล็อต ยิ่งกล่องยาว ความแปรปรวนก็จะยิ่งสูงขึ้น ตัวอย่างเช่น เราจะเห็นว่าความแปรปรวนจะสูงขึ้นเล็กน้อยสำหรับผู้เข้าร่วมในโปรแกรม C เมื่อเปรียบเทียบกับโปรแกรม A และโปรแกรม B

2. ทำการทดสอบ Bartlett

 #Create box plots that show distribution of weight loss for each group
bartlett. test (weight_loss ~ program, data=data)

#Bartlett test of homogeneity of variances
#
#data: weight_loss by program
#Bartlett's K-squared = 8.2713, df = 2, p-value = 0.01599

การทดสอบ Bartlett จะทดสอบสมมติฐานว่างที่ว่ากลุ่มตัวอย่างมีความแปรปรวนเท่ากัน เทียบกับสมมติฐานทางเลือกที่ว่ากลุ่มตัวอย่างมีความแปรปรวนไม่เท่ากัน ในกรณีนี้ ค่า p ของการทดสอบคือ 0.01599 ซึ่งต่ำกว่าระดับอัลฟ่าที่ 0.05 นี่แสดงให้เห็นว่าตัวอย่างทั้งหมดไม่ได้มีความแปรปรวนเหมือนกัน

จะทำอย่างไรถ้าสมมติฐานนี้ไม่ได้รับการเคารพ:

โดยทั่วไป การวิเคราะห์ความแปรปรวนแบบทางเดียวถือว่าค่อนข้างแข็งแกร่งสำหรับการละเมิดสมมติฐานความแปรปรวนที่เท่ากัน ตราบใดที่แต่ละกลุ่มมีขนาดกลุ่มตัวอย่างเท่ากัน

อย่างไรก็ตาม หากขนาดตัวอย่างไม่เท่ากันและข้อสันนิษฐานนี้ถูกละเมิดอย่างรุนแรง คุณสามารถเรียกใช้ การทดสอบ Kruskal-Wallis แทน ซึ่งเป็นเวอร์ชัน ANOVA แบบไม่มีพารามิเตอร์

สมมติฐาน #3: ความเป็นอิสระ

ANOVA ถือว่า:

• การสังเกตของแต่ละกลุ่มไม่ขึ้นอยู่กับการสังเกตของกลุ่มอื่นๆ ทั้งหมด
• การสังเกตภายในแต่ละกลุ่มได้มาจากการสุ่มตัวอย่าง

วิธีตรวจสอบสมมติฐานนี้:

ไม่มีการทดสอบอย่างเป็นทางการที่คุณสามารถใช้เพื่อตรวจสอบว่าการสังเกตในแต่ละกลุ่มมีความเป็นอิสระและได้มาจากการสุ่มตัวอย่าง วิธีเดียวที่จะเป็นไปตามสมมติฐานนี้คือการใช้การออกแบบแบบสุ่ม

จะทำอย่างไรถ้าสมมติฐานนี้ไม่ได้รับการเคารพ:

น่าเสียดายที่คุณไม่สามารถทำอะไรได้มากนักหากไม่เป็นไปตามสมมติฐานนี้ พูดง่ายๆ คือ หากรวบรวมข้อมูลในลักษณะที่การสังเกตในแต่ละกลุ่มไม่เป็นอิสระจากการสังเกตในกลุ่มอื่น หรือหากการสังเกตภายในแต่ละกลุ่มไม่ได้มาจากกระบวนการสุ่ม ผลลัพธ์ ANOVA จะไม่น่าเชื่อถือ .

หากไม่เป็นไปตามสมมติฐานนี้ วิธีที่ดีที่สุดคือสร้างการทดสอบขึ้นใหม่โดยใช้การออกแบบแบบสุ่ม

อ่านเพิ่มเติม:

วิธีดำเนินการวิเคราะห์ความแปรปรวนแบบทางเดียวใน R
วิธีการดำเนินการวิเคราะห์ความแปรปรวนแบบทางเดียวใน Excel