วิธีการคำนวณความสัมพันธ์อันดับสเปียร์แมนใน excel

ในทางสถิติ ความสัมพันธ์ หมายถึงจุดแข็งและทิศทางของความสัมพันธ์ระหว่างตัวแปรสองตัว ค่าของสัมประสิทธิ์สหสัมพันธ์สามารถอยู่ในช่วงตั้งแต่ -1 ถึง 1 โดยมีการตีความดังต่อไปนี้:

• -1: ความสัมพันธ์เชิงลบที่สมบูรณ์แบบระหว่างตัวแปรสองตัว
• 0: ไม่มีความสัมพันธ์ระหว่างตัวแปรสองตัว
• 1: ความสัมพันธ์เชิงบวกที่สมบูรณ์แบบระหว่างสองตัวแปร

ความสัมพันธ์แบบพิเศษเรียกว่า Spearman’s rank correlation ซึ่งใช้ในการวัดความสัมพันธ์ระหว่างตัวแปรอันดับ 2 ตัว (เช่น อันดับคะแนนสอบคณิตศาสตร์ของนักเรียนสัมพันธ์กับอันดับคะแนนสอบวิทยาศาสตร์ในชั้นเรียน)

บทช่วยสอนนี้จะอธิบายวิธีคำนวณความสัมพันธ์อันดับ Spearman ระหว่างตัวแปรสองตัวใน Excel

ตัวอย่าง: สหสัมพันธ์อันดับสเปียร์แมนใน Excel

ทำตามขั้นตอนต่อไปนี้เพื่อคำนวณความสัมพันธ์อันดับสเปียร์แมนระหว่างคะแนนสอบคณิตศาสตร์และคะแนนสอบวิทยาศาสตร์ของนักเรียน 10 คนในชั้นเรียนใดชั้นเรียนหนึ่ง

ขั้นตอนที่ 1: ป้อนข้อมูล

ป้อนผลการสอบของนักเรียนแต่ละคนในสองคอลัมน์แยกกัน:

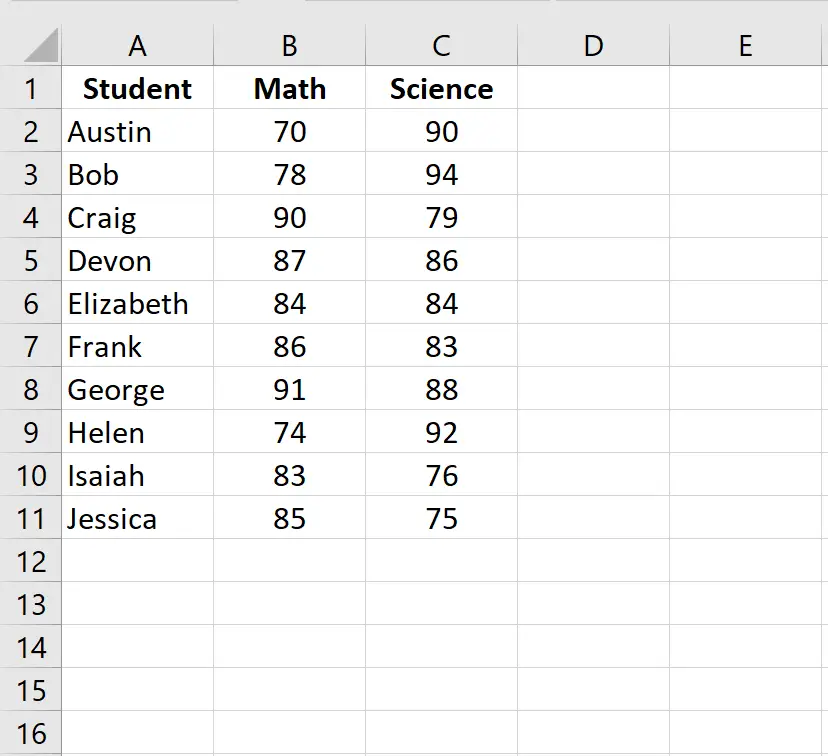
ขั้นตอนที่ 2: คำนวณอันดับสำหรับคะแนนสอบแต่ละรายการ

ต่อไปเราจะคำนวณอันดับคะแนนสอบแต่ละรายการ ใช้สูตรต่อไปนี้ในเซลล์ D2 และ E2 เพื่อคำนวณอันดับทางคณิตศาสตร์และวิทยาศาสตร์สำหรับนักเรียนคนแรก ออสติน:

เซลล์ D2: =RANK.AVG(B2, $B$2:$B$11, 0)

เซลล์ E2: =RANK.AVG(C2, $C$2:$C$11, 0)

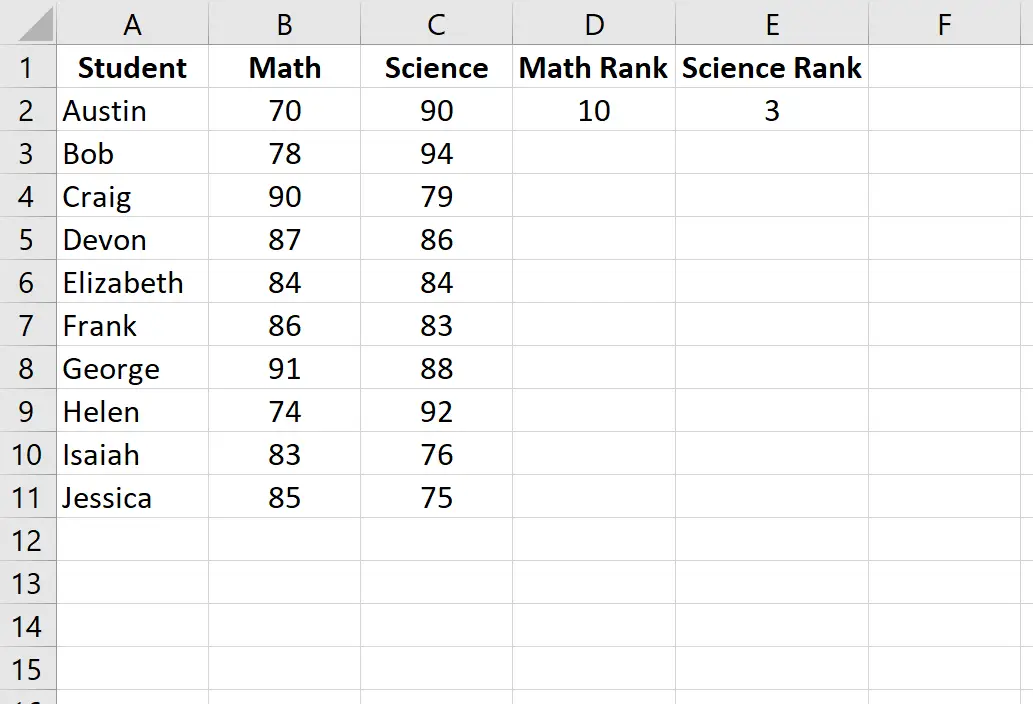
จากนั้น ไฮไลต์เซลล์ที่เหลือเพื่อเติม:

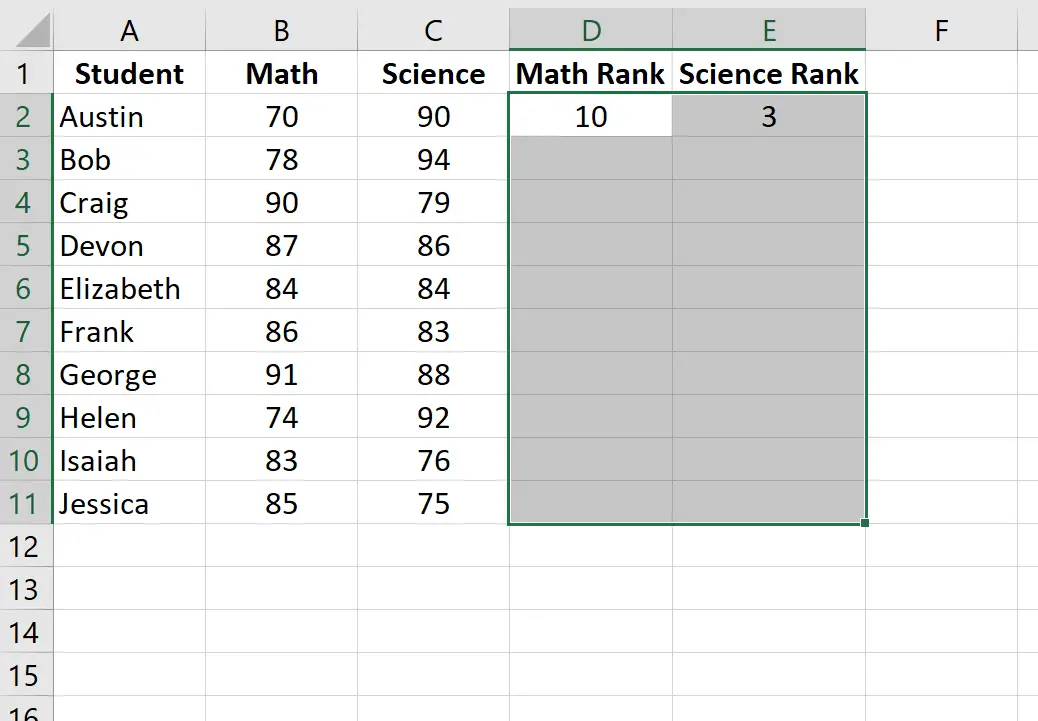
จากนั้นคลิก Ctrl+D เพื่อเข้าสู่อันดับของนักเรียนแต่ละคน:

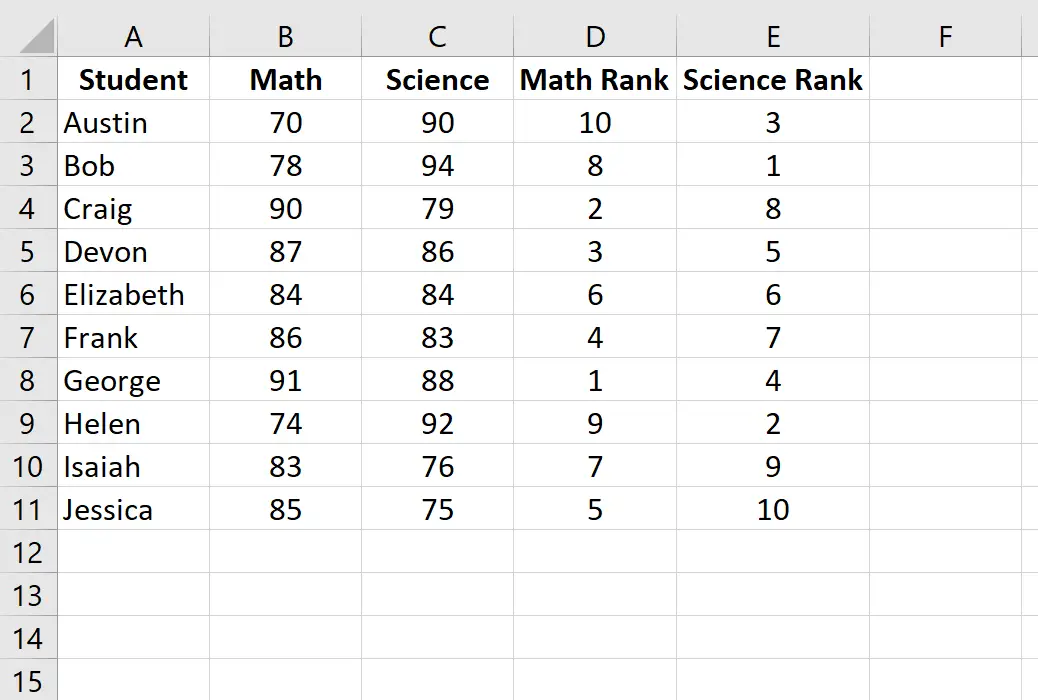
ขั้นตอนที่ 3: คำนวณค่าสัมประสิทธิ์สหสัมพันธ์อันดับสเปียร์แมน

สุดท้ายนี้ เราจะคำนวณค่าสัมประสิทธิ์สหสัมพันธ์อันดับสเปียร์แมนระหว่างคะแนนทางคณิตศาสตร์และคะแนนวิทยาศาสตร์โดยใช้ฟังก์ชัน CORREL()

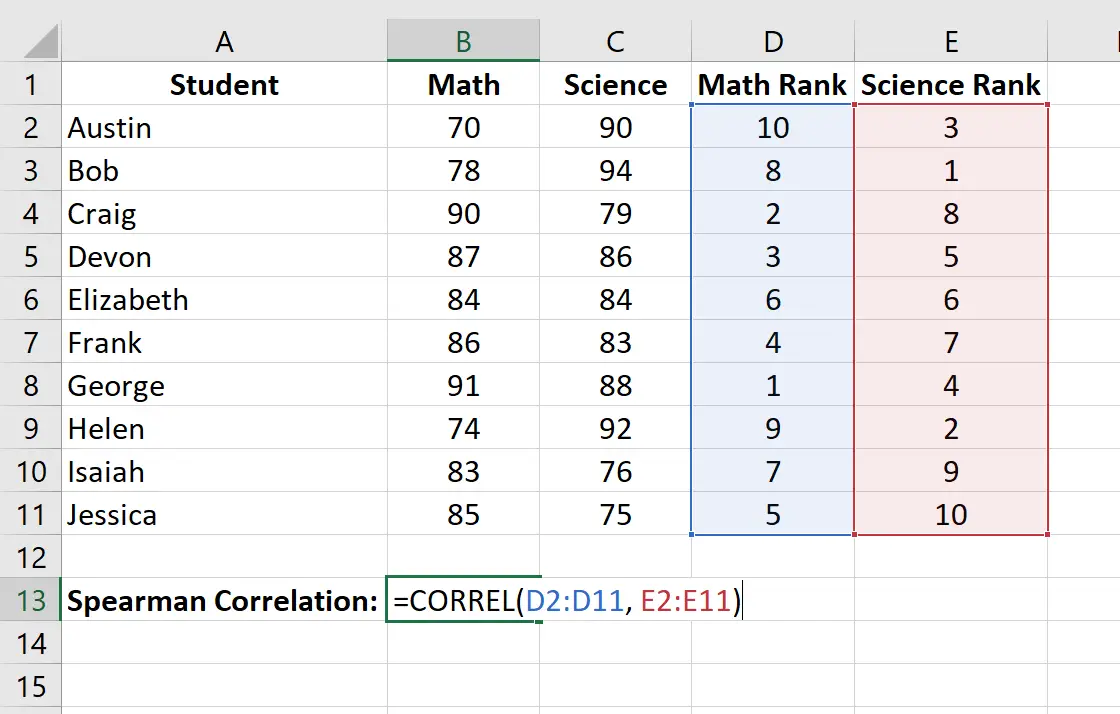
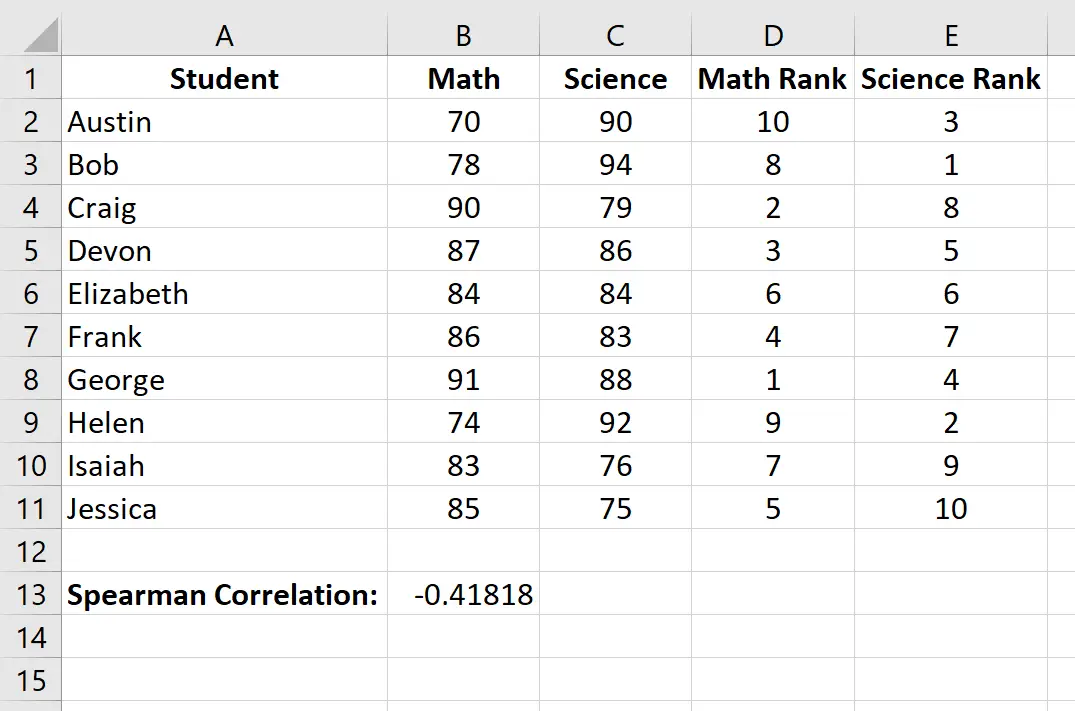
ความสัมพันธ์อันดับ Spearman กลายเป็น -0.41818

ขั้นตอนที่ 4 (ไม่บังคับ): พิจารณาว่าความสัมพันธ์ของอันดับ Spearman มีนัยสำคัญทางสถิติหรือไม่

ในขั้นตอนที่แล้ว เราพบว่าความสัมพันธ์อันดับ Spearman ระหว่างคะแนนสอบคณิตศาสตร์และวิทยาศาสตร์คือ -0.41818 ซึ่งบ่งชี้ความสัมพันธ์เชิงลบระหว่างตัวแปรทั้งสอง

อย่างไรก็ตาม เพื่อตรวจสอบว่าความสัมพันธ์นี้มีนัยสำคัญทางสถิติหรือไม่ เราจะต้องอ้างอิงตารางความสัมพันธ์อันดับ Spearman ของค่าวิกฤต ซึ่งแสดงค่าวิกฤตที่เกี่ยวข้องกับขนาดตัวอย่างที่แตกต่างกัน (n) และระดับนัยสำคัญ (α)

หากค่าสัมบูรณ์ของสัมประสิทธิ์สหสัมพันธ์ของเรามากกว่าค่าวิกฤตในตาราง แสดงว่าความสัมพันธ์ระหว่างตัวแปรทั้งสองนั้นมีนัยสำคัญทางสถิติ

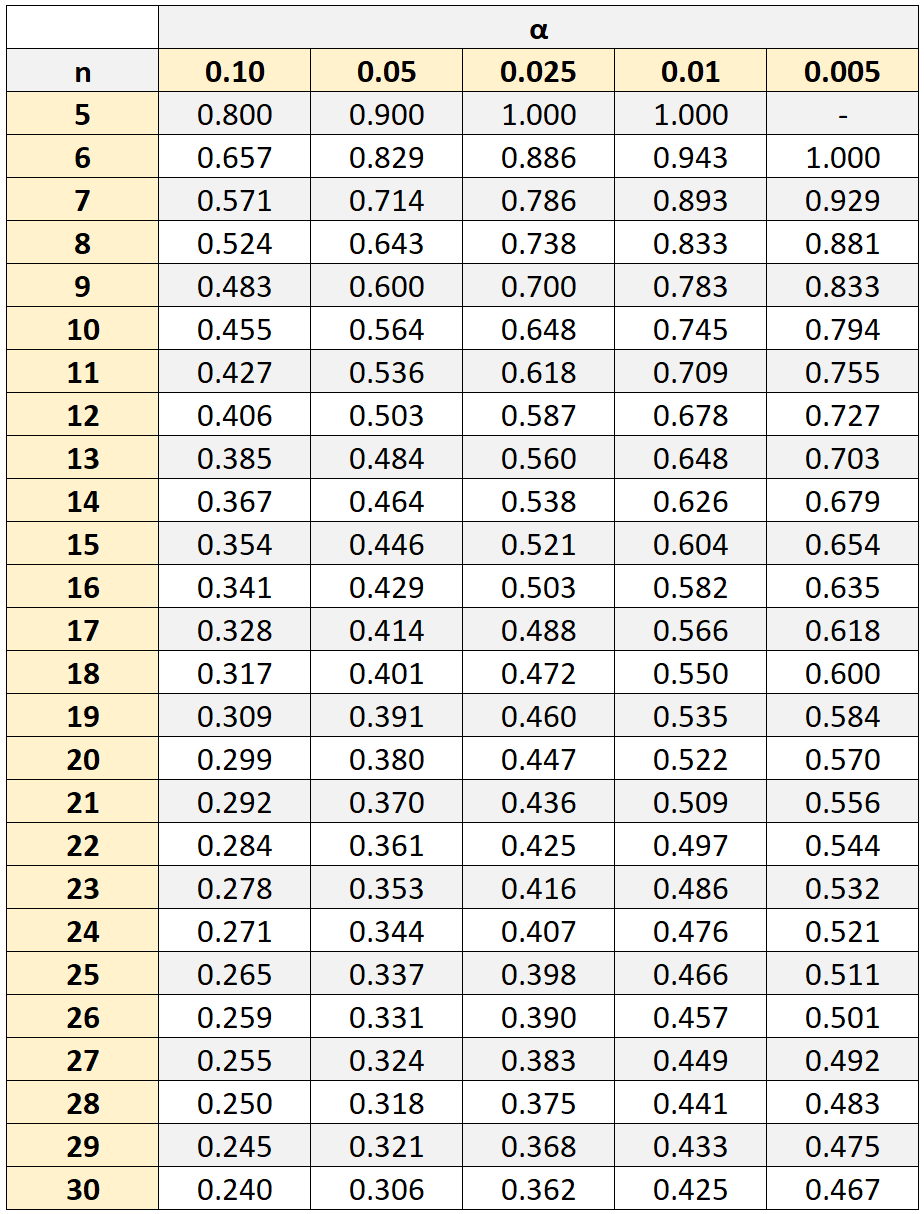
ในตัวอย่างของเรา ขนาดของกลุ่มตัวอย่างคือ n = นักเรียน 10 คน เมื่อใช้ระดับนัยสำคัญ 0.05 เราพบว่าค่าวิกฤตคือ 0.564

เนื่องจากค่าสัมบูรณ์ของค่าสัมประสิทธิ์สหสัมพันธ์อันดับสเปียร์แมนที่เราคำนวณ ( 0.41818 ) ไม่มากกว่าค่าวิกฤตนี้ ซึ่งหมายความว่าความสัมพันธ์ระหว่างคะแนนคณิตศาสตร์และวิทยาศาสตร์ไม่มีนัยสำคัญทางสถิติ