สัมประสิทธิ์สหสัมพันธ์เพียร์สัน

โดย ดร.เบนจามิน แอนเดอร์สัน สิงหาคม 5, 2023 สถิติ 0 ความคิดเห็น

บทความนี้จะอธิบายว่าสัมประสิทธิ์สหสัมพันธ์แบบเพียร์สัน (หรือสัมประสิทธิ์สหสัมพันธ์เชิงเส้น) คืออะไร และใช้เพื่ออะไร คุณจะค้นพบวิธีคำนวณค่าสัมประสิทธิ์สหสัมพันธ์ของเพียร์สันพร้อมกับแบบฝึกหัดทีละขั้นตอน นอกจากนี้ คุณสามารถค้นหาค่าสัมประสิทธิ์สหสัมพันธ์เพียร์สันของชุดข้อมูลใดๆ ได้ด้วยเครื่องคิดเลขออนไลน์ในตอนท้าย

ค่าสัมประสิทธิ์สหสัมพันธ์ของเพียร์สันคืออะไร?

ค่าสัมประสิทธิ์สหสัมพันธ์แบบเพียร์สัน หรือเรียกอีกอย่างว่า ค่าสัมประสิทธิ์สหสัมพันธ์เชิงเส้น หรือเรียกง่ายๆ ว่า ค่าสัมประสิทธิ์สหสัมพันธ์ เป็นหน่วยวัดทางสถิติที่ระบุความสัมพันธ์ระหว่างตัวแปรสองตัว

ในการคำนวณค่าสัมประสิทธิ์สหสัมพันธ์แบบเพียร์สันระหว่างตัวแปรสองตัว คุณต้องหารความแปรปรวนร่วมของตัวแปรดังกล่าวด้วยรากที่สองของผลคูณของความแปรปรวน

ดังนั้น ค่าสัมประสิทธิ์สหสัมพันธ์ของเพียร์สันจึงพยายามหาปริมาณการพึ่งพาเชิงเส้นระหว่างตัวแปรสุ่มเชิงปริมาณสองตัว นิรนัย, ในการประเมินความสัมพันธ์ระหว่างตัวแปรเป็นตัวเลขนั้นมีความซับซ้อนเนื่องจากเป็นการยากที่จะตัดสินว่าคู่ของตัวแปรมีความสัมพันธ์กันมากขึ้นระหว่างถ้า, เช่นเดียวกับใน pues, วัตถุของสัมประสิทธิ์สหสัมพันธ์ของเพียร์สันคือการประเมินค่าความสัมพันธ์ระหว่างตัวแปรเพื่อให้สามารถ เปรียบเทียบระหว่างพวกเขา

ค่าของดัชนีสหสัมพันธ์ของ Pearson อยู่ระหว่าง -1 ถึง +1 เราจะดูด้านล่างว่าค่าของสัมประสิทธิ์สหสัมพันธ์เพียร์สันถูกตีความอย่างไร

สูตรสัมประสิทธิ์สหสัมพันธ์เพียร์สัน

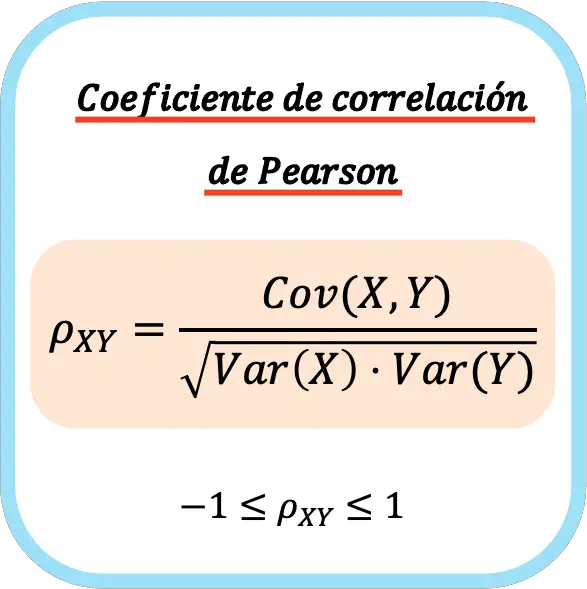
ค่าสัมประสิทธิ์สหสัมพันธ์แบบเพียร์สันของตัวแปรทางสถิติสองตัวจะเท่ากับผลหารระหว่างความแปรปรวนร่วมของตัวแปรกับรากที่สองของผลคูณของความแปรปรวนของตัวแปรแต่ละตัว

ดังนั้นสูตรในการคำนวณค่าสัมประสิทธิ์สหสัมพันธ์เพียร์สันจึงเป็นดังนี้:

สัมประสิทธิ์สหสัมพันธ์เพียร์สัน สัมประสิทธิ์สหสัมพันธ์เชิงเส้น

👉 คุณสามารถใช้เครื่องคิดเลขด้านล่างเพื่อคำนวณค่าสัมประสิทธิ์สหสัมพันธ์แบบเพียร์สันสำหรับชุดข้อมูลใดก็ได้

เมื่อคำนวณค่าสัมประสิทธิ์สหสัมพันธ์แบบเพียร์สันกับประชากร โดยทั่วไปจะแสดงด้วยอักษรกรีก ρ แต่เมื่อคำนวณสัมประสิทธิ์สัมพันธ์กับตัวอย่าง โดยปกติจะใช้ตัวอักษร r เป็นสัญลักษณ์

โปรดจำไว้ว่าในการหาค่าสัมประสิทธิ์สหสัมพันธ์แบบเพียร์สัน จำเป็นอย่างยิ่งที่คุณจะต้องรู้วิธีคำนวณความแปรปรวนร่วมระหว่างตัวแปรสองตัวและความแปรปรวนของตัวแปร นอกจากนี้ คุณต้องเข้าใจว่าการวัดทางสถิติเหล่านี้หมายถึงอะไร ดังนั้นก่อนที่จะอธิบายต่อขอแนะนำให้อ่านบทความสองบทความต่อไปนี้:

➤ ดู: วิธีคำนวณความแปรปรวนร่วม
➤ ดู: วิธีคำนวณช่องว่าง

ตัวอย่างการคำนวณสัมประสิทธิ์สหสัมพันธ์เพียร์สัน

เมื่อพิจารณาคำจำกัดความของสัมประสิทธิ์สหสัมพันธ์ของเพียร์สันและสูตรแล้ว ด้านล่างนี้คือตัวอย่างทีละขั้นตอนเพื่อให้คุณเห็นว่าค่าสัมประสิทธิ์สหสัมพันธ์คำนวณอย่างไร

คำนวณสัมประสิทธิ์สหสัมพันธ์เพียร์สันระหว่างตัวแปรต่อเนื่องสองตัวต่อไปนี้:

ก่อนที่จะคำนวณค่าสัมประสิทธิ์สหสัมพันธ์ของเพียร์สัน เราจะแสดงชุดข้อมูลในแผนภาพกระจายเพื่อวิเคราะห์ความสัมพันธ์ระหว่างตัวแปรทั้งสอง:

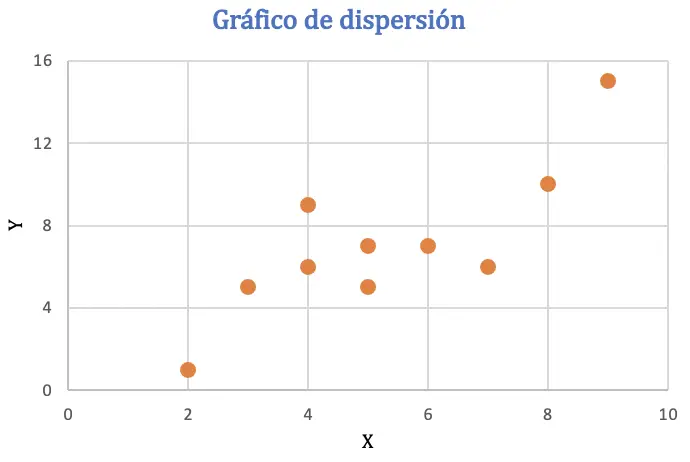
จากแผนภาพกระจาย สามารถอนุมานได้ว่าข้อมูลอาจมีแนวโน้มเชิงบวก หรือกล่าวอีกนัยหนึ่ง เมื่อตัวแปรตัวหนึ่งมีค่าเพิ่มขึ้น ตัวแปรอีกตัวก็จะเพิ่มขึ้นตามไปด้วย เพื่อตรวจสอบความสัมพันธ์ เราจะหาค่าสัมประสิทธิ์เพียร์สัน

สิ่งแรกที่ต้องทำคือหาค่าเฉลี่ยเลขคณิตของแต่ละตัวแปรแยกกัน ซึ่งเท่ากับผลรวมของข้อมูลหารด้วยจำนวนการสังเกต

$\overline{x}=\cfrac{\displaystyle \sum_{i=1}^n x_i}{n}=\cfrac{53}{10}=5,3$

$\overline{y}=\cfrac{\displaystyle \sum_{i=1}^n y_i}{n}=\cfrac{71}{10}=7,1$

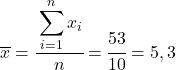
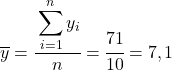
ตอนนี้เราทราบค่าเฉลี่ยของตัวแปรแต่ละตัวแล้ว เราต้องเพิ่มคอลัมน์ต่อไปนี้ลงในตารางข้อมูล:

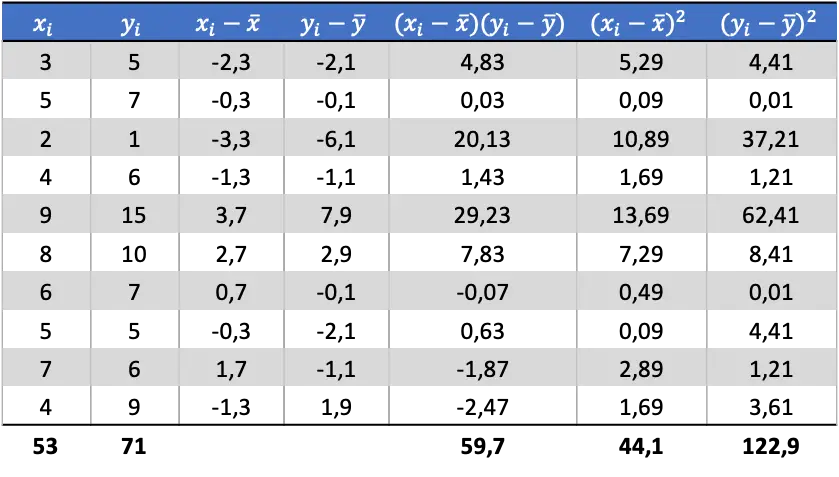
ตารางข้อมูลการคำนวณค่าสัมประสิทธิ์เพียร์สัน

จากข้อมูลที่คำนวณในตาราง เราจะกำหนดค่าของความแปรปรวนร่วมและความแปรปรวน (หากคุณจำไม่ได้ว่าทำอย่างไร มีลิงก์สองลิงก์ด้านบนซึ่งมีการอธิบายโดยละเอียด):

$Cov(X,Y)=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{n}=\cfrac{59,7}{10}=5,97$

$Var(X)=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{x}\right)^2}{n}=\cfrac{44,1}{10}=4,41$

$Var(Y)=\cfrac{\displaystyle\sum_{i=1}^n\left(y_i-\overline{y}\right)^2}{n}=\cfrac{122,9}{10}=12,29$

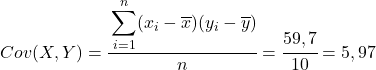
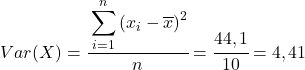
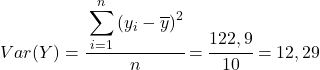
สุดท้าย เพียงใช้สูตรสัมประสิทธิ์สหสัมพันธ์แบบเพียร์สันเพื่อให้ได้ค่า:

$\rho_{XY}=\cfrac{Cov(X,Y)}{\sqrt{Var(X)\cdot Var(Y)}}=\cfrac{5,97}{\sqrt{4,41\cdot 12,29}}=0,81$

ค่าสัมประสิทธิ์สหสัมพันธ์แบบเพียร์สันมีค่าใกล้เคียงกับ 1 มาก ซึ่งหมายความว่าตัวแปรทั้งสองนี้มีความสัมพันธ์เชิงบวกที่ค่อนข้างแข็งแกร่ง

อย่างที่คุณเห็นแล้ว เพื่อกำหนดค่าสัมประสิทธิ์สหสัมพันธ์ของเพียร์สัน การใช้โปรแกรมเช่น Excel เพื่อทำการคำนวณคอลัมน์ได้รวดเร็วยิ่งขึ้นจะมีประโยชน์มาก

เครื่องคำนวณสัมประสิทธิ์สหสัมพันธ์เพียร์สัน

ใส่ชุดข้อมูลทางสถิติลงในเครื่องคิดเลขต่อไปนี้เพื่อคำนวณค่าสัมประสิทธิ์สหสัมพันธ์แบบเพียร์สันระหว่างตัวแปรสองตัว คุณต้องแยกคู่ข้อมูลเพื่อให้ในกล่องแรกมีเพียงค่าของตัวแปรตัวเดียวและในกล่องที่สองมีเพียงค่าของตัวแปรตัวที่สองเท่านั้น

ข้อมูลต้องคั่นด้วยช่องว่างและป้อนโดยใช้จุดเป็นตัวคั่นทศนิยม

การตีความค่าสัมประสิทธิ์สหสัมพันธ์เพียร์สัน

ในส่วนนี้ เราจะมาดูวิธีตีความค่าสัมประสิทธิ์สหสัมพันธ์แบบเพียร์สัน เนื่องจากค่าสัมประสิทธิ์สหสัมพันธ์ของเพียร์สันยังไม่เพียงพอ แต่คุณต้องรู้วิธีวิเคราะห์ความหมายของค่าสัมประสิทธิ์สหสัมพันธ์ด้วย

ดังนั้น การตีความค่าสัมประสิทธิ์สหสัมพันธ์แบบเพียร์สัน จึงขึ้นอยู่กับค่าของมัน:

r=-1 : ตัวแปรทั้งสองมีความสัมพันธ์เชิงลบที่สมบูรณ์แบบ ดังนั้นเราจึงสามารถวาดเส้นที่มีความชันเป็นลบโดยที่จุดทั้งหมดเชื่อมโยงกัน
-1<r<0 : ความสัมพันธ์ระหว่างตัวแปรทั้งสองนั้นเป็นลบ ดังนั้นเมื่อตัวแปรตัวหนึ่งเพิ่มขึ้น อีกตัวแปรหนึ่งก็จะลดลง ยิ่งค่าเข้าใกล้ -1 มากเท่าใด ตัวแปรก็จะยิ่งมีความสัมพันธ์เชิงลบมากขึ้นเท่านั้น
r=0 : ความสัมพันธ์ระหว่างตัวแปรทั้งสองนั้นอ่อนแอมาก จริงๆ แล้วความสัมพันธ์เชิงเส้นระหว่างตัวแปรทั้งสองนั้นเป็นศูนย์ นี่ไม่ได้หมายความว่าตัวแปรมีความเป็นอิสระ เนื่องจากตัวแปรเหล่านั้นอาจมีความสัมพันธ์แบบไม่เชิงเส้นได้
0<r<1 : ความสัมพันธ์ระหว่างตัวแปรทั้งสองเป็นค่าบวก ยิ่งค่าเข้าใกล้ +1 มากเท่าใด ความสัมพันธ์ระหว่างตัวแปรก็จะยิ่งแข็งแกร่งขึ้นเท่านั้น ในกรณีนี้ ตัวแปรตัวหนึ่งมีแนวโน้มที่จะเพิ่มมูลค่าเมื่ออีกตัวแปรหนึ่งเพิ่มขึ้นเช่นกัน
r=1 : ตัวแปรทั้งสองมีความสัมพันธ์เชิงบวกที่สมบูรณ์แบบ กล่าวคือ ตัวแปรทั้งสองมีความสัมพันธ์เชิงเส้นเชิงบวก

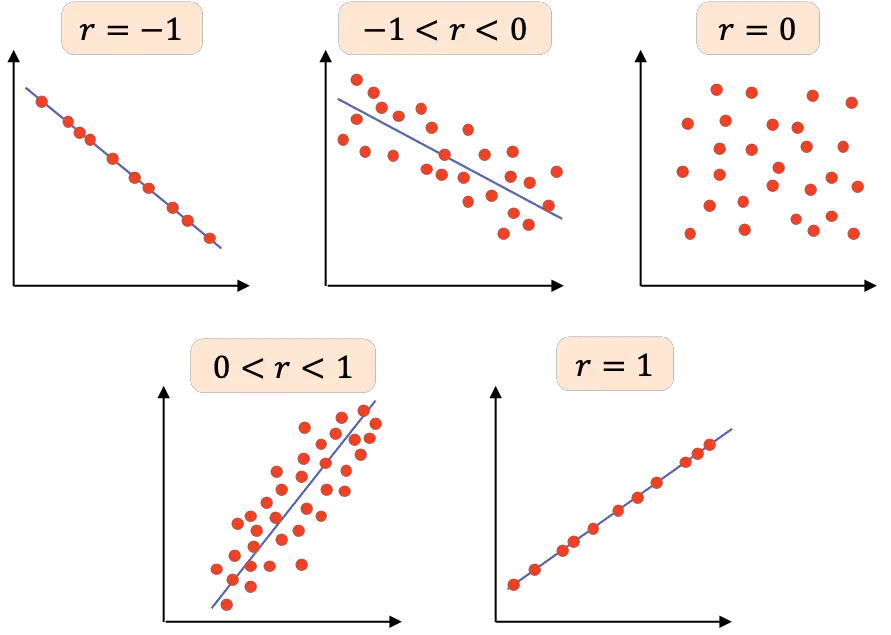
การตีความค่าสัมประสิทธิ์สหสัมพันธ์เพียร์สัน

โดยสรุป ตารางต่อไปนี้นำเสนอการตีความค่าสัมประสิทธิ์สหสัมพันธ์แบบเพียร์สันแบบต่างๆ:

ค่า	การตีความ
ร=-1	ความสัมพันธ์เชิงลบที่สมบูรณ์แบบ
-1<r<0	ความสัมพันธ์เชิงลบ: ยิ่งความสัมพันธ์เข้าใกล้ -1 มากเท่าไรก็ยิ่งแข็งแกร่งเท่านั้น
ร=0	ความสัมพันธ์เชิงเส้นเป็นศูนย์
0<r<1	ความสัมพันธ์เชิงบวก: ยิ่งความสัมพันธ์เข้าใกล้ +1 มากเท่าไรก็ยิ่งแข็งแกร่งเท่านั้น
ร=1	ความสัมพันธ์เชิงบวกที่สมบูรณ์แบบ

โปรดทราบว่าแม้ว่าจะมีความสัมพันธ์ระหว่างตัวแปรสองตัว แต่ก็ไม่ได้หมายความว่ามีสาเหตุ ระหว่างตัวแปรทั้งสอง กล่าวคือ ความสัมพันธ์ระหว่างตัวแปรสองตัวไม่ได้หมายความว่าการเปลี่ยนแปลงในตัวแปรเป็นสาเหตุของการเปลี่ยนแปลงของตัวแปร ตัวแปรอื่น ๆ

ตัวอย่างเช่น ถ้าเราพบว่ามีความสัมพันธ์เชิงบวกระหว่างการผลิตฮอร์โมนที่แตกต่างกันสองชนิดในร่างกาย การเพิ่มขึ้นของฮอร์โมนตัวหนึ่งก็ไม่จำเป็นที่จะทำให้ฮอร์โมนอีกตัวหนึ่งเพิ่มขึ้น อาจเป็นไปได้ว่าร่างกายผลิตฮอร์โมนทั้งสองตัวเพราะต้องต่อสู้กับความเจ็บป่วยจึงทำให้ระดับฮอร์โมนทั้งสองเพิ่มขึ้นพร้อมกัน ซึ่งสาเหตุอาจมาจากความเจ็บป่วย เพื่อตรวจสอบว่ามีความเชื่อมโยงเชิงสาเหตุระหว่างฮอร์โมนทั้งสองชนิดนี้หรือไม่ ควรมีการศึกษาเพิ่มเติม

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

สวัสดี ฉันชื่อเบนจามิน ศาสตราจารย์สถิติเกษียณอายุแล้ว และผันตัวมาเป็นครูสอนสถิติโดยเฉพาะ ด้วยประสบการณ์และความเชี่ยวชาญที่กว้างขวางในสาขาสถิติ ฉันกระตือรือร้นที่จะแบ่งปันความรู้ของฉันเพื่อเสริมศักยภาพนักเรียนผ่าน Statorials. รู้เพิ่มเติม