ค่าเบี่ยงเบนมาตรฐานและข้อผิดพลาดมาตรฐาน: อะไรคือความแตกต่าง?

คำสองคำที่นักเรียนมักสับสนในสถิติคือ ค่าเบี่ยงเบนมาตรฐาน และ ข้อผิดพลาดมาตรฐาน

ค่าเบี่ยงเบนมาตรฐาน วัดการกระจายของค่าในชุดข้อมูล

ข้อผิดพลาดมาตรฐาน คือค่าเบี่ยงเบนมาตรฐานของค่าเฉลี่ยตัวอย่างซ้ำจากประชากร

ลองดูตัวอย่างเพื่ออธิบายแนวคิดนี้ให้ชัดเจน

ตัวอย่าง: ส่วนเบี่ยงเบนมาตรฐานกับข้อผิดพลาดมาตรฐาน

สมมติว่าเราวัดน้ำหนักของเต่า 10 ตัวที่แตกต่างกัน

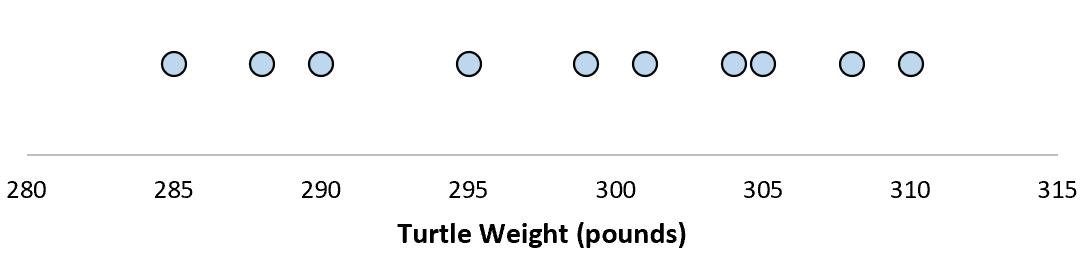
สำหรับเต่าตัวอย่าง 10 ตัวนี้ เราสามารถคำนวณค่าเฉลี่ยตัวอย่างและค่าเบี่ยงเบนมาตรฐานของกลุ่มตัวอย่างได้:

สมมติว่าค่าเบี่ยงเบนมาตรฐานคือ 8.68 สิ่งนี้ทำให้เรามีแนวคิดเกี่ยวกับการกระจายน้ำหนักของเต่าเหล่านี้

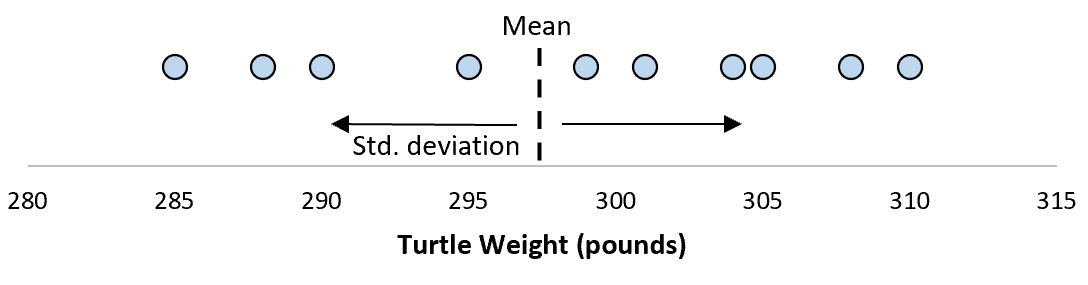
แต่สมมติว่าเราสุ่มตัวอย่างเต่า 10 ตัว แบบสุ่ม อีกตัวอย่างหนึ่งแล้วทำการวัดด้วย

มีความเป็นไปได้มากกว่าที่เต่าตัวอย่าง 10 ตัวนี้จะมีค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐานแตกต่างกันเล็กน้อย แม้ว่าจะมาจากประชากรเดียวกัน:

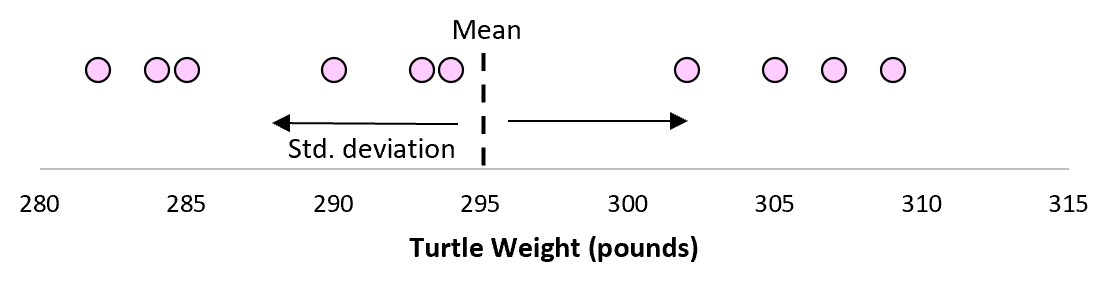
ทีนี้ ถ้าเราจินตนาการว่าเราสุ่มตัวอย่างซ้ำจากประชากรกลุ่มเดียวกัน และบันทึกค่าเฉลี่ยตัวอย่างและส่วนเบี่ยงเบนมาตรฐานตัวอย่างสำหรับแต่ละตัวอย่าง:

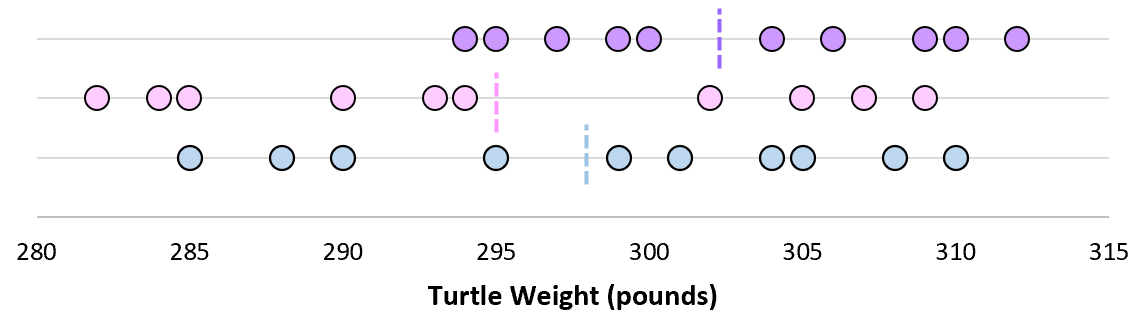
ทีนี้ลองจินตนาการว่าเราพลอตค่าเฉลี่ยตัวอย่างแต่ละค่าในบรรทัดเดียวกัน:

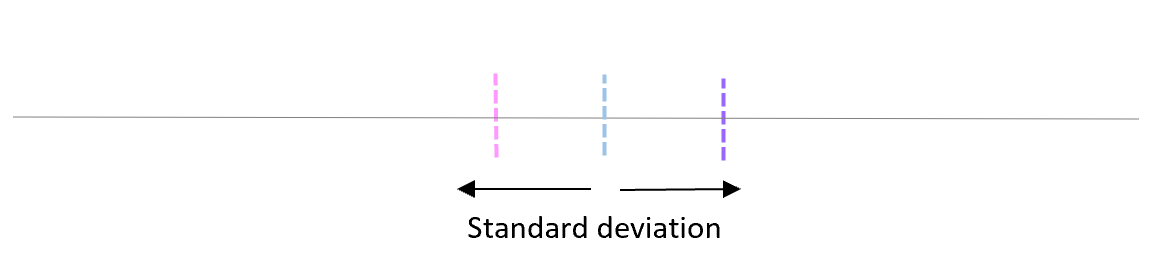
ค่าเบี่ยงเบนมาตรฐานของค่าเฉลี่ยเหล่านี้เรียกว่าค่าคลาดเคลื่อนมาตรฐาน

สูตรในการคำนวณข้อผิดพลาดมาตรฐานคือ:

ค่าคลาดเคลื่อนมาตรฐาน = s/ √ n

ทอง:

• s: ค่าเบี่ยงเบนมาตรฐานตัวอย่าง
• n: ขนาดตัวอย่าง

การใช้ข้อผิดพลาดมาตรฐานมีประโยชน์อย่างไร

เมื่อเราคำนวณค่าเฉลี่ยของกลุ่มตัวอย่างที่กำหนด จริงๆ แล้วเราไม่ได้ต้องการทราบค่าเฉลี่ยของกลุ่มตัวอย่างนั้น แต่เป็นค่าเฉลี่ยของประชากรกลุ่มใหญ่ที่กลุ่มตัวอย่างมา

อย่างไรก็ตาม เราใช้ตัวอย่างเนื่องจากรวบรวมข้อมูลได้ง่ายกว่าประชากรทั้งหมดมาก

และแน่นอนว่า ค่าเฉลี่ยตัวอย่างแตกต่างกันไปในแต่ละตัวอย่าง ดังนั้นเราจึงใช้ค่า คลาดเคลื่อนมาตรฐานของค่าเฉลี่ย เป็นวิธีวัดความแม่นยำของการประมาณค่าเฉลี่ยของเรา

คุณจะสังเกตเห็นในสูตรสำหรับคำนวณข้อผิดพลาดมาตรฐานว่าเมื่อขนาดตัวอย่าง (n) เพิ่มขึ้น ข้อผิดพลาดมาตรฐานจะลดลง:

ค่าคลาดเคลื่อนมาตรฐาน = s/ √ n

นี่น่าจะสมเหตุสมผล เพราะตัวอย่างที่ใหญ่ขึ้นจะลดความแปรปรวน และเพิ่มโอกาสที่ค่าเฉลี่ยตัวอย่างจะเข้าใกล้ค่าเฉลี่ยประชากรจริงมากขึ้น

เมื่อใดควรใช้ส่วนเบี่ยงเบนมาตรฐานกับข้อผิดพลาดมาตรฐาน

ถ้าเราเพียงต้องการวัดการกระจายของค่าในชุดข้อมูล เราก็สามารถใช้ ค่าเบี่ยงเบนมาตรฐาน ได้

อย่างไรก็ตาม หากเราต้องการหาปริมาณความไม่แน่นอนของการประมาณค่าเฉลี่ย เราสามารถใช้ ค่าคลาดเคลื่อนมาตรฐานของค่าเฉลี่ย ได้

ขึ้นอยู่กับสถานการณ์เฉพาะของคุณและสิ่งที่คุณพยายามทำให้สำเร็จ คุณอาจเลือกใช้ค่าเบี่ยงเบนมาตรฐานหรือข้อผิดพลาดมาตรฐาน