ข้อมูลเบื้องต้นเกี่ยวกับ ancova (การวิเคราะห์ความแปรปรวน)

ANCOVA ย่อมาจาก “การวิเคราะห์ความแปรปรวนร่วม” เพื่อให้เข้าใจวิธีการทำงานของ ANCOVA จะต้องเข้าใจ ANOVA ก่อน

การ วิเคราะห์ความแปรปรวน   (การวิเคราะห์ความแปรปรวน) ใช้เพื่อพิจารณาว่ามีความแตกต่างที่มีนัยสำคัญทางสถิติระหว่างค่าเฉลี่ยของกลุ่มอิสระสามกลุ่มขึ้นไปหรือไม่

ตัวอย่างเช่น สมมติว่าเราต้องการทราบว่าเทคนิคการเรียนส่งผลต่อคะแนนสอบของนักเรียนในชั้นเรียนหรือไม่ เราแบ่งชั้นเรียนออกเป็นสามกลุ่มโดยการสุ่ม แต่ละกลุ่มใช้เทคนิคการเรียนที่แตกต่างกันเป็นเวลาหนึ่งเดือนเพื่อเตรียมตัวสอบ สิ้นเดือนนักเรียนทุกคนจะสอบเหมือนกัน

หากต้องการทราบว่าเทคนิคการเรียนรู้มีผลกระทบต่อคะแนนสอบหรือไม่ เราสามารถใช้การวิเคราะห์ความแปรปรวนแบบทางเดียว ซึ่งจะบอกเราว่ามีความแตกต่างที่มีนัยสำคัญทางสถิติระหว่างคะแนนเฉลี่ยของทั้งสามกลุ่มหรือไม่

ANCOVA เป็นส่วนขยายของ ANOVA ซึ่งเราต้องการตรวจสอบว่ามีความแตกต่างที่มีนัยสำคัญทางสถิติระหว่างกลุ่มอิสระสามกลุ่มขึ้นไป หรือไม่ หลังจากพิจารณา ตัวแปร ร่วมหนึ่งตัวขึ้นไป

ตัวแปรร่วม เป็นตัวแปรต่อเนื่องที่แปรผันตามตัวแปรตอบสนอง

เช่น สมมติว่าเราต้องการทราบว่าเทคนิคการเรียนมีผลกระทบต่อคะแนนสอบหรือไม่ แต่เราต้องการคำนึงถึงเกรดที่นักเรียนมีอยู่แล้วในชั้นเรียนด้วย เราสามารถใช้เกรดปัจจุบันเป็นตัวแปรร่วมและดำเนินการ ANCOVA เพื่อพิจารณาว่ามีความแตกต่างที่มีนัยสำคัญทางสถิติระหว่างคะแนนสอบเฉลี่ยของทั้งสามกลุ่มหรือไม่

สิ่งนี้ช่วยให้เราทดสอบได้ว่าเทคนิคการศึกษามีผลกระทบต่อคะแนนสอบหรือไม่เมื่ออิทธิพลของตัวแปรร่วมถูกลบออกแล้ว

ดังนั้น หากเราพบว่าคะแนนสอบระหว่างเทคนิคการศึกษาทั้งสามเทคนิคมีความแตกต่างที่มีนัยสำคัญทางสถิติ เราก็มั่นใจได้ว่าความแตกต่างนี้จะยังคงอยู่ แม้จะพิจารณาเกรดปัจจุบันของนักเรียนในชั้นเรียนแล้วก็ตาม (ค ‘นั่นคือ ถ้าพวกเขา กำลังไปได้ดีอยู่แล้ว หรือถ้าพวกเขากำลังไปได้ดีอยู่แล้ว) ไม่อยู่ในชั้นเรียน) .

สมมติฐานของ ANCOVA

ก่อนดำเนินการ ANCOVA สิ่งสำคัญคือต้องแน่ใจว่าเป็นไปตามสมมติฐานต่อไปนี้:

• ตัวแปรร่วมและตัวแปรแฟคเตอร์มีความเป็นอิสระ – ตัวแปรร่วมและตัวแปรแฟคเตอร์จะต้องเป็นอิสระจากกัน เนื่องจากการเพิ่มคำศัพท์ความแปรปรวนร่วมในแบบจำลองจะเหมาะสมก็ต่อเมื่อตัวแปรร่วมและตัวแปรแฟคเตอร์ทำหน้าที่อย่างเป็นอิสระต่อกัน ตัวแปรตอบสนอง
• ตัวแปรร่วมเป็นข้อมูลที่ต่อเนื่องกัน โควาเรียตจะต้องต่อเนื่องกัน (เช่น ข้อมูลช่วงเวลาหรืออัตราส่วน)
• ความสม่ำเสมอของความแปรปรวน – ความแปรปรวนระหว่างกลุ่มควรจะเท่ากันโดยประมาณ
• ความเป็นอิสระ – การสังเกตในแต่ละกลุ่มจะต้องเป็นอิสระ
• ความปกติ – ข้อมูลควรมีการกระจายโดยประมาณตามปกติในแต่ละกลุ่ม
• ไม่มีค่าผิดปกติที่รุนแรง – ไม่ควรมีค่าผิดปกติที่รุนแรงในกลุ่มใดๆ ที่อาจส่งผลกระทบอย่างมีนัยสำคัญต่อผลลัพธ์ของ ANCOVA

อันโควา: ตัวอย่าง

ครูคนหนึ่งต้องการทราบว่าเทคนิคการเรียนที่แตกต่างกันสามแบบส่งผลต่อคะแนนสอบหรือไม่ แต่เธอต้องการคำนึงถึงเกรดปัจจุบันที่นักเรียนมีอยู่แล้วในชั้นเรียนด้วย

โดยจะดำเนินการ ANCOVA โดยใช้ตัวแปรต่อไปนี้:

• ตัวแปรปัจจัย: การศึกษาทางเทคนิค
• Covariate: คะแนนปัจจุบัน
• ตัวแปรตอบสนอง: คะแนนสอบ

ตารางต่อไปนี้แสดงชุดข้อมูลของนักเรียน 15 คนที่ได้รับคัดเลือกให้เข้าร่วมในการศึกษานี้:

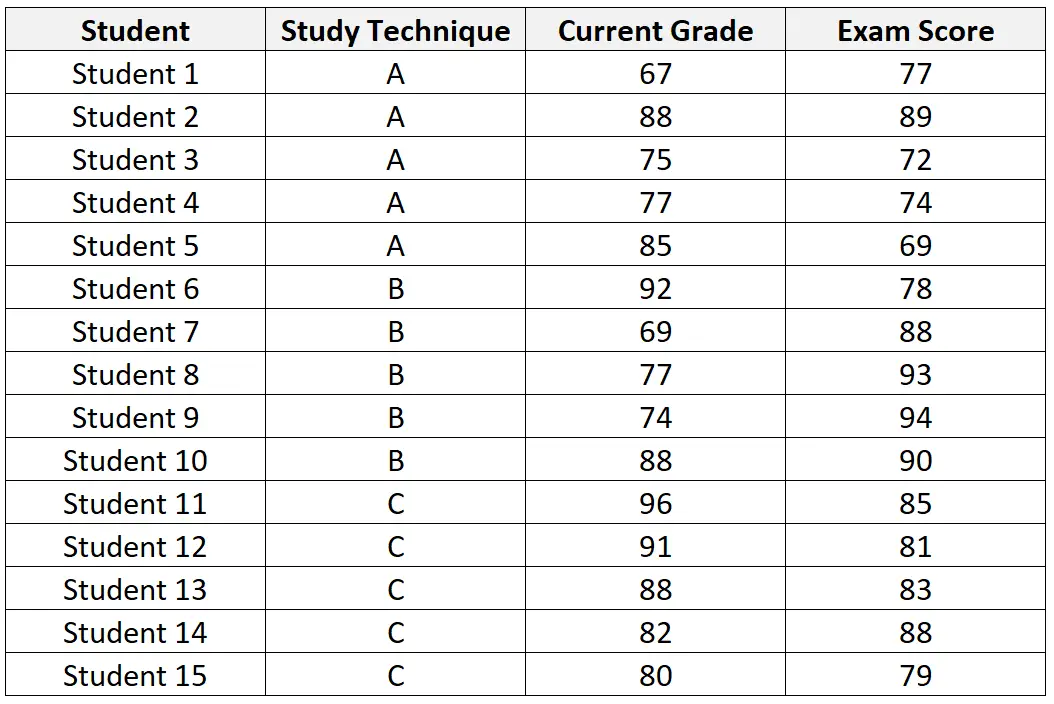
หลังจากดำเนินการ ANCOVA กับชุดข้อมูลแล้ว ครูจะได้รับผลลัพธ์ดังต่อไปนี้:

ค่า p สำหรับเทคนิคการศึกษาคือ 0.03155 เนื่องจากค่านี้น้อยกว่า 0.05 เราจึงสามารถปฏิเสธสมมติฐานว่างที่ว่าเทคนิคการศึกษาแต่ละเทคนิคทำให้ได้คะแนนสอบเฉลี่ยเท่ากัน แม้ว่าจะพิจารณาเกรดปัจจุบันของนักเรียนในชั้นเรียนแล้วก็ตาม

เพื่อพิจารณาว่าเทคนิคการศึกษาใดที่ทำให้คะแนนสอบเฉลี่ยแตกต่างกัน ครูจะต้องทำการ ทดสอบหลังการทดลอง

แหล่งข้อมูลเพิ่มเติม

วิธีดำเนินการ ANCOVA ใน Excel
วิธีดำเนินการ ANCOVA ใน R
วิธีดำเนินการ ANCOVA ใน Python
ความแตกต่างระหว่าง ANOVA, ANCOVA, MANOVA และ MANCOVA