ประชากรหมายถึง
บทความนี้จะอธิบายว่าประชากรหมายถึงอะไรในสถิติ ในทำนองเดียวกัน คุณจะพบว่าสูตรสำหรับค่าเฉลี่ยประชากรคืออะไร ช่วงความเชื่อมั่นของค่าเฉลี่ยประชากรคำนวณอย่างไร และยิ่งไปกว่านั้น อะไรคือความแตกต่างระหว่างค่าเฉลี่ยประชากรกับค่าเฉลี่ยของ ‘ตัวอย่าง’
ประชากรเฉลี่ยเป็นเท่าไร?
ค่าเฉลี่ยประชากร คือค่าเฉลี่ยเลขคณิตขององค์ประกอบทั้งหมดของประชากรทางสถิติ ดังนั้นในการคำนวณค่าเฉลี่ยประชากรจะต้องบวกค่าประชากรทั้งหมดแล้วหารด้วยจำนวนองค์ประกอบทั้งหมดในประชากร
สัญลักษณ์ของค่าเฉลี่ยประชากรคืออักษรกรีก μ
ในทำนองเดียวกัน ค่าเฉลี่ยประชากรสามารถกำหนดเป็น ค่าคาดหวัง ของตัวแปรที่แสดงถึงประชากรได้
วิธีการคำนวณค่าเฉลี่ยประชากร
เมื่อเราทราบคำจำกัดความของค่าเฉลี่ยประชากรแล้ว เรามาดูกันว่าค่าเฉลี่ยประชากรคำนวณอย่างไรเพื่อให้เข้าใจความหมายของมันได้ดีขึ้น
หากทราบค่าทั้งหมดในประชากรทางสถิติ ควรใช้สูตรค่าเฉลี่ยเลขคณิตเพื่อคำนวณค่าเฉลี่ยประชากร ดังนั้นในกรณีนี้ ในการคำนวณค่าเฉลี่ยประชากร เราจำเป็นต้องบวกค่าประชากรทั้งหมดแล้วหารด้วยจำนวนข้อมูลทั้งหมด
ดังนั้น ถ้าเราทราบมูลค่าขององค์ประกอบทั้งหมดของประชากร สูตรในการคำนวณค่าเฉลี่ยประชากร จะเป็นดังนี้
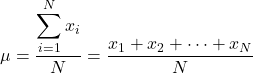
อย่างไรก็ตาม โดยทั่วไปไม่ทราบค่าประชากรทั้งหมด ดังนั้น โดยปกติแล้วค่าของค่าเฉลี่ยประชากร จะประมาณเป็นช่วงๆ
ช่วงความเชื่อมั่นสำหรับค่าเฉลี่ยประชากร
ในทางปฏิบัติ เป็นไปไม่ได้ที่จะศึกษาบุคคลทั้งหมดในประชากรกลุ่มหนึ่ง ดังนั้น โดยปกติแล้วจะมีการสุ่มตัวอย่างประชากร และทำการประมาณค่าของค่าเฉลี่ยประชากรตามค่าของมัน แม่นยำยิ่งขึ้น เราคำนวณช่วงเวลาที่ค่าเฉลี่ยของประชากรทั้งหมดมีแนวโน้มที่จะโกหก ช่วงนี้เรียกว่าช่วงความเชื่อมั่นของค่าเฉลี่ยประชากร
ช่วงความเชื่อมั่น สำหรับค่าเฉลี่ยประชากรคำนวณโดยการบวกและลบออกจากค่าเฉลี่ยตัวอย่าง ค่าของ Z α/2 คูณด้วยค่าเบี่ยงเบนมาตรฐาน (σ) และหารด้วยรากที่สองของความสูงของตัวอย่าง (n) ดังนั้น สูตรในการคำนวณช่วงความเชื่อมั่นของค่าเฉลี่ยประชากรคือ
![]()
สูตรข้างต้นจะใช้เมื่อทราบความแปรปรวนของประชากร อย่างไรก็ตาม หากไม่ทราบความแปรปรวนของประชากร ซึ่งเป็นกรณีที่พบบ่อยที่สุด ช่วงความเชื่อมั่นสำหรับค่าเฉลี่ยจะคำนวณโดยใช้สูตรต่อไปนี้
![]()
ทอง:
-

คือค่าเฉลี่ยตัวอย่าง
-

คือค่าของการแจกแจง t ของดีกรีอิสระ n-1 ด้วยความน่าจะเป็น α/2 ของนักเรียน สำหรับกลุ่มตัวอย่างขนาดใหญ่และระดับความเชื่อมั่น 95% มักจะใกล้กับ 1.96 และสำหรับระดับความเชื่อมั่น 99% มักจะใกล้กับ 2.576
-

คือค่าเบี่ยงเบนมาตรฐานตัวอย่าง
-

คือขนาดตัวอย่าง
ค่าเฉลี่ยประชากรและค่าเฉลี่ยตัวอย่าง
สุดท้ายนี้ โดยสรุป เราจะทบทวนความแตกต่างระหว่างค่าเฉลี่ยประชากรและค่าเฉลี่ยตัวอย่าง เพื่อให้แนวคิดทางสถิติทั้งสองนี้มีความชัดเจน
ความแตกต่างระหว่างค่าเฉลี่ยประชากรและค่าเฉลี่ยตัวอย่าง คือช่วงของค่าที่คำนวณค่าเฉลี่ย ค่าเฉลี่ยประชากรคือค่าเฉลี่ยของประชากรทางสถิติทั้งหมด ในขณะที่ค่าเฉลี่ยตัวอย่างคือค่าเฉลี่ยของกลุ่มตัวอย่างในประชากร
นอกจากนี้ เพื่อแยกความแตกต่างของค่าเฉลี่ยประชากรจากค่าเฉลี่ยตัวอย่าง จะใช้สัญลักษณ์ที่ต่างกันแทน สัญลักษณ์หมายถึงค่าเฉลี่ยประชากรคือ
![]()
ในทางกลับกัน สัญลักษณ์ของค่าเฉลี่ยตัวอย่างคือ
![]()
.
![Rendered by QuickLaTeX.com \begin{array}{c}\mu =\text{Media poblacional}\\[2ex]\overline{x} = \text{Media muestral}\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-f812349b186d7c1a8abdd1d2807f0a60_l3.png)
หากคุณยังคงมีข้อสงสัยเกี่ยวกับความแตกต่างระหว่างค่าเฉลี่ยทั้งสองประเภทนี้ หรือต้องการทราบข้อมูลเพิ่มเติมเกี่ยวกับการคำนวณค่าเฉลี่ยตัวอย่าง คุณสามารถอ่านบทความต่อไปนี้: