วิธีดำเนินการ ols regression ใน python (พร้อมตัวอย่าง)

การถดถอยกำลังสองน้อยที่สุดสามัญ (OLS) เป็นวิธีการที่ช่วยให้เราค้นหาเส้นที่อธิบายความสัมพันธ์ระหว่างตัวแปรทำนายหนึ่งตัวหรือมากกว่ากับ ตัวแปรตอบสนอง ได้ดีที่สุด

วิธีนี้ช่วยให้เราสามารถค้นหาสมการต่อไปนี้:

ŷ = ข ₀ + ข ₁ x

ทอง:

• ŷ : ค่าตอบกลับโดยประมาณ
• b ₀ : ต้นกำเนิดของเส้นถดถอย
• b ₁ : ความชันของเส้นถดถอย

สมการนี้สามารถช่วยให้เราเข้าใจความสัมพันธ์ระหว่างตัวทำนายและตัวแปรตอบสนอง และสามารถใช้เพื่อทำนายค่าของตัวแปรตอบสนองตามค่าของตัวแปรทำนายได้

ตัวอย่างทีละขั้นตอนต่อไปนี้แสดงวิธีการถดถอย OLS ใน Python

ขั้นตอนที่ 1: สร้างข้อมูล

สำหรับตัวอย่างนี้ เราจะสร้างชุดข้อมูลที่ประกอบด้วยตัวแปรสองตัวต่อไปนี้สำหรับนักเรียน 15 คน:

• จำนวนชั่วโมงเรียนทั้งหมด
• ผลสอบ

เราจะทำการถดถอย OLS โดยใช้ชั่วโมงเป็นตัวแปรทำนายและคะแนนสอบเป็นตัวแปรตอบสนอง

รหัสต่อไปนี้แสดงวิธีสร้างชุดข้อมูลปลอมในแพนด้า:

 import pandas as pd

#createDataFrame
df = pd. DataFrame ({' hours ': [1, 2, 4, 5, 5, 6, 6, 7, 8, 10, 11, 11, 12, 12, 14],
                   ' score ': [64, 66, 76, 73, 74, 81, 83, 82, 80, 88, 84, 82, 91, 93, 89]})

#view DataFrame
print (df)

    hours score
0 1 64
1 2 66
2 4 76
3 5 73
4 5 74
5 6 81
6 6 83
7 7 82
8 8 80
9 10 88
10 11 84
11 11 82
12 12 91
13 12 93
14 14 89

ขั้นตอนที่ 2: ดำเนินการถดถอย OLS

ต่อไป เราสามารถใช้ฟังก์ชันในโมดูล statsmodels เพื่อดำเนินการถดถอย OLS โดยใช้ ชั่วโมง เป็นตัวแปรทำนายและให้คะแนนเป็นตัวแปร ตอบสนอง :

 import statsmodels.api as sm

#define predictor and response variables
y = df[' score ']
x = df[' hours ']

#add constant to predictor variables
x = sm. add_constant (x)

#fit linear regression model
model = sm. OLS (y,x). fit ()

#view model summary
print ( model.summary ())

                            OLS Regression Results                            
==================================================== ============================
Dept. Variable: R-squared score: 0.831
Model: OLS Adj. R-squared: 0.818
Method: Least Squares F-statistic: 63.91
Date: Fri, 26 Aug 2022 Prob (F-statistic): 2.25e-06
Time: 10:42:24 Log-Likelihood: -39,594
No. Observations: 15 AIC: 83.19
Df Residuals: 13 BIC: 84.60
Model: 1                                         
Covariance Type: non-robust                                         
==================================================== ============================
                 coef std err t P>|t| [0.025 0.975]
-------------------------------------------------- ----------------------------
const 65.3340 2.106 31.023 0.000 60.784 69.884
hours 1.9824 0.248 7.995 0.000 1.447 2.518
==================================================== ============================
Omnibus: 4,351 Durbin-Watson: 1,677
Prob(Omnibus): 0.114 Jarque-Bera (JB): 1.329
Skew: 0.092 Prob(JB): 0.515
Kurtosis: 1.554 Cond. No. 19.2
==================================================== ============================

จากคอลัมน์ coef เราจะเห็นค่าสัมประสิทธิ์การถดถอยและเขียนสมการการถดถอยแบบพอดีต่อไปนี้:

คะแนน = 65.334 + 1.9824*(ชั่วโมง)

ซึ่งหมายความว่าแต่ละชั่วโมงที่เรียนเพิ่มเติมจะสัมพันธ์กับคะแนนสอบเฉลี่ยที่เพิ่มขึ้น 1.9824 คะแนน

ค่าเดิมที่ 65,334 บอกเราถึงคะแนนสอบโดยเฉลี่ยที่คาดหวังสำหรับนักเรียนที่เรียนเป็นเวลา 0 ชั่วโมง

นอกจากนี้เรายังสามารถใช้สมการนี้เพื่อค้นหาคะแนนสอบที่คาดหวังโดยพิจารณาจากจำนวนชั่วโมงที่นักเรียนเรียน

เช่น นักเรียนที่เรียน 10 ชั่วโมง ควรได้คะแนนสอบ 85.158 :

คะแนน = 65.334 + 1.9824*(10) = 85.158

ต่อไปนี้เป็นวิธีการตีความสรุปแบบจำลองที่เหลือ:

• P(>|t|): นี่คือค่า p ที่เกี่ยวข้องกับค่าสัมประสิทธิ์แบบจำลอง เนื่องจากค่า p สำหรับ ชั่วโมง (0.000) น้อยกว่า 0.05 เราจึงสามารถพูดได้ว่ามีความสัมพันธ์ที่มีนัยสำคัญทางสถิติระหว่าง ชั่วโมง และ คะแนน
• R-squared: ค่านี้บอกเราว่าเปอร์เซ็นต์ของความแปรผันของคะแนนสอบสามารถอธิบายได้ด้วยจำนวนชั่วโมงที่เรียน ในกรณีนี้ 83.1% ของความแปรผันของคะแนนสามารถอธิบายได้ด้วยจำนวนชั่วโมงที่ศึกษา
• สถิติ F และค่า p: สถิติ F ( 63.91 ) และค่า p ที่สอดคล้องกัน ( 2.25e-06 ) บอกเราถึงความสำคัญโดยรวมของแบบจำลองการถดถอย กล่าวคือ ตัวแปรตัวทำนายในแบบจำลองนั้นมีประโยชน์ในการอธิบายการเปลี่ยนแปลงหรือไม่ ในตัวแปรตอบสนอง เนื่องจากค่า p ในตัวอย่างนี้น้อยกว่า 0.05 แบบจำลองของเราจึงมีนัยสำคัญทางสถิติ และ ชั่วโมง จึงถือว่ามีประโยชน์ในการอธิบายความแปรผันของ คะแนน

ขั้นตอนที่ 3: เห็นภาพเส้นที่เหมาะสมที่สุด

สุดท้ายนี้ เราสามารถใช้แพ็คเกจการแสดงข้อมูล Matplotlib เพื่อแสดงภาพเส้นการถดถอยที่พอดีกับจุดข้อมูลจริง:

 import matplotlib. pyplot as plt

#find line of best fit
a, b = np. polyfit (df[' hours '], df[' score '], 1 )

#add points to plot
plt. scatter (df[' hours '], df[' score '], color=' purple ')

#add line of best fit to plot
plt. plot (df[' hours '], a*df[' hours ']+b)

#add fitted regression equation to plot
plt. text ( 1 , 90 , 'y = ' + '{:.3f}'.format(b) + ' + {:.3f}'.format(a) + 'x', size= 12 )

#add axis labels
plt. xlabel (' Hours Studied ')
plt. ylabel (' Exam Score ')

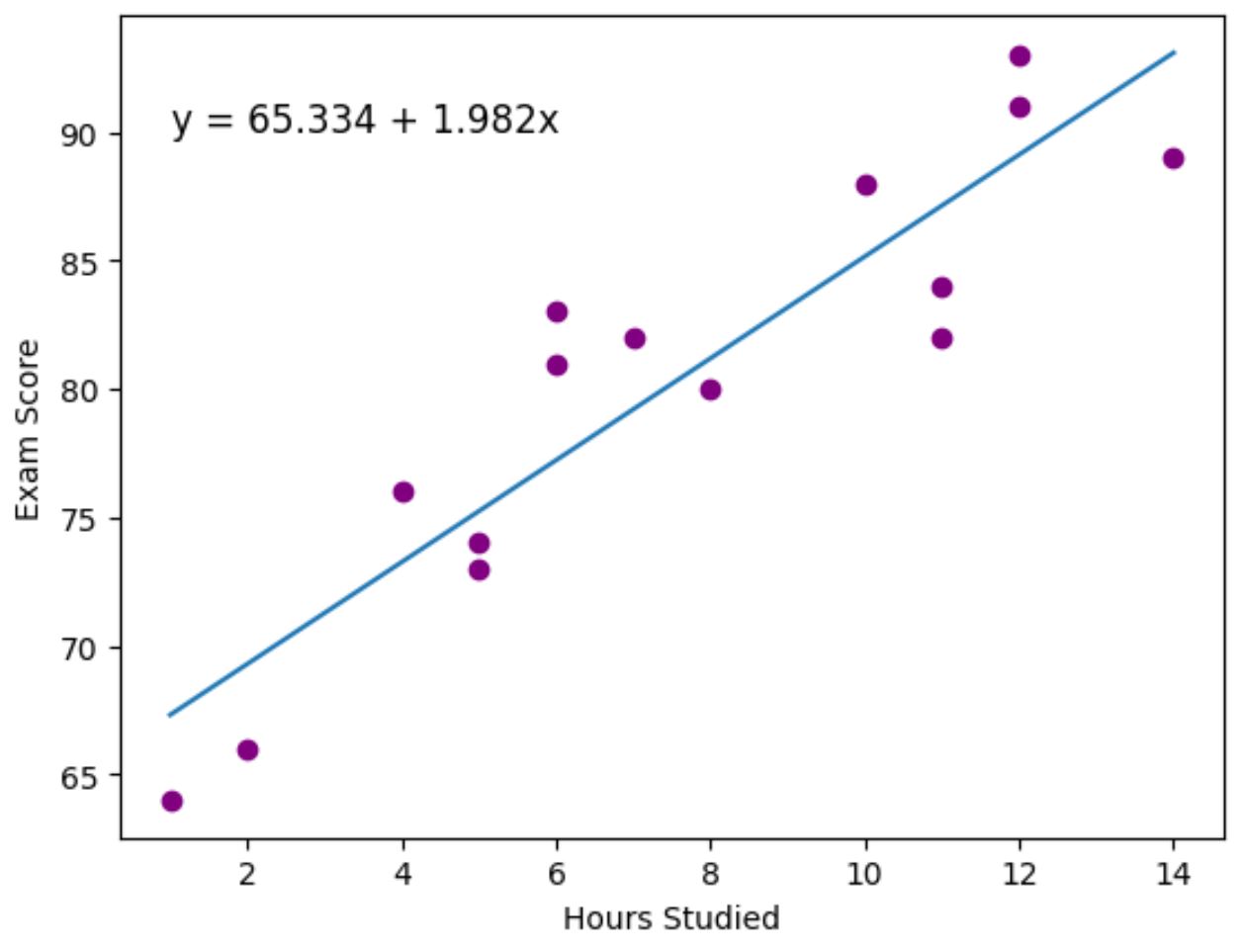
จุดสีม่วงแสดงถึงจุดข้อมูลจริง และเส้นสีน้ำเงินแสดงถึงเส้นถดถอยที่ติดตั้งไว้

นอกจากนี้เรายังใช้ฟังก์ชัน plt.text() เพื่อเพิ่มสมการถดถอยที่พอดีไว้ที่มุมซ้ายบนของโครงเรื่อง

เมื่อดูกราฟ ปรากฏว่าเส้นถดถอยพอดีจับความสัมพันธ์ระหว่างตัวแปร ชั่วโมง และตัวแปร คะแนน ได้ค่อนข้างดี

แหล่งข้อมูลเพิ่มเติม

บทช่วยสอนต่อไปนี้จะอธิบายวิธีทำงานทั่วไปอื่นๆ ใน Python:

วิธีการดำเนินการถดถอยโลจิสติกใน Python
วิธีการดำเนินการถดถอยเอ็กซ์โปเนนเชียลใน Python
วิธีการคำนวณ AIC ของตัวแบบการถดถอยใน Python