วิธีดำเนินการถดถอยกำลังสองใน python

การถดถอยกำลังสอง คือการถดถอยประเภทหนึ่งที่เราสามารถใช้เพื่อหาปริมาณความสัมพันธ์ระหว่างตัวแปรทำนายและตัวแปรตอบสนอง เมื่อความสัมพันธ์ที่แท้จริงเป็นแบบกำลังสอง ซึ่งอาจมีลักษณะเหมือน “U” หรือ “U” กลับหัวบนกราฟ

กล่าวคือ เมื่อตัวแปรทำนายเพิ่มขึ้น ตัวแปรตอบสนองก็มีแนวโน้มที่จะเพิ่มขึ้นเช่นกัน แต่หลังจากจุดหนึ่ง ตัวแปรตอบสนองก็เริ่มลดลงเมื่อตัวแปรทำนายยังคงเพิ่มขึ้นต่อไป

บทช่วยสอนนี้จะอธิบายวิธีการถดถอยกำลังสองใน Python

ตัวอย่าง: การถดถอยกำลังสองใน Python

สมมติว่าเรามีข้อมูลเกี่ยวกับจำนวนชั่วโมงทำงานต่อสัปดาห์และรายงานระดับความสุข (ในระดับ 0 ถึง 100) สำหรับคน 16 คน:

 import numpy as np
import scipy.stats as stats

#define variables
hours = [6, 9, 12, 12, 15, 21, 24, 24, 27, 30, 36, 39, 45, 48, 57, 60]
happ = [12, 18, 30, 42, 48, 78, 90, 96, 96, 90, 84, 78, 66, 54, 36, 24]

หากเราสร้างแผนภาพกระจายอย่างง่ายของข้อมูลนี้ เราจะเห็นว่าความสัมพันธ์ระหว่างตัวแปรทั้งสองนั้นมีรูปตัว “U”:

 import matplotlib.pyplot as plt

#create scatterplot
plt.scatter(hours, happ) 

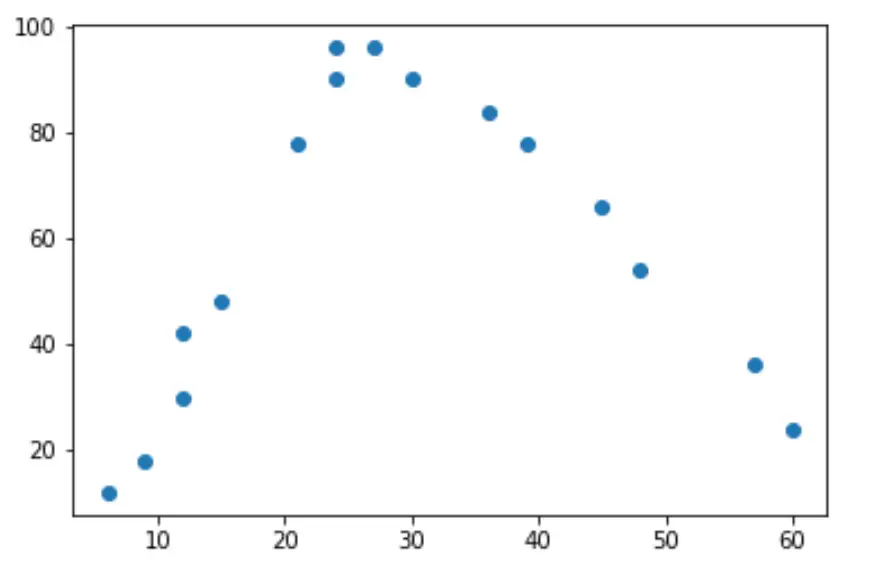
เมื่อชั่วโมงทำงานเพิ่มขึ้น ความสุขก็เพิ่มขึ้น แต่เมื่อชั่วโมงทำงานเกิน 35 ชั่วโมงต่อสัปดาห์ ความสุขก็เริ่มลดลง

เนื่องจากรูปร่าง “U” นี้ หมายความว่าการถดถอยกำลังสองน่าจะเป็นตัวเลือกที่ดีในการหาความสัมพันธ์ระหว่างตัวแปรทั้งสอง

หากต้องการทำการถดถอยกำลังสองจริงๆ เราสามารถใส่แบบจำลองการถดถอยพหุนามที่มีดีกรี 2 ได้โดยใช้ ฟังก์ชัน numpy.polyfit() :

 import numpy as np

#polynomial fit with degree = 2
model = np.poly1d(np.polyfit(hours, happ, 2))

#add fitted polynomial line to scatterplot
polyline = np.linspace(1, 60, 50)
plt.scatter(hours, happ)
plt.plot(polyline, model(polyline))
plt.show() 

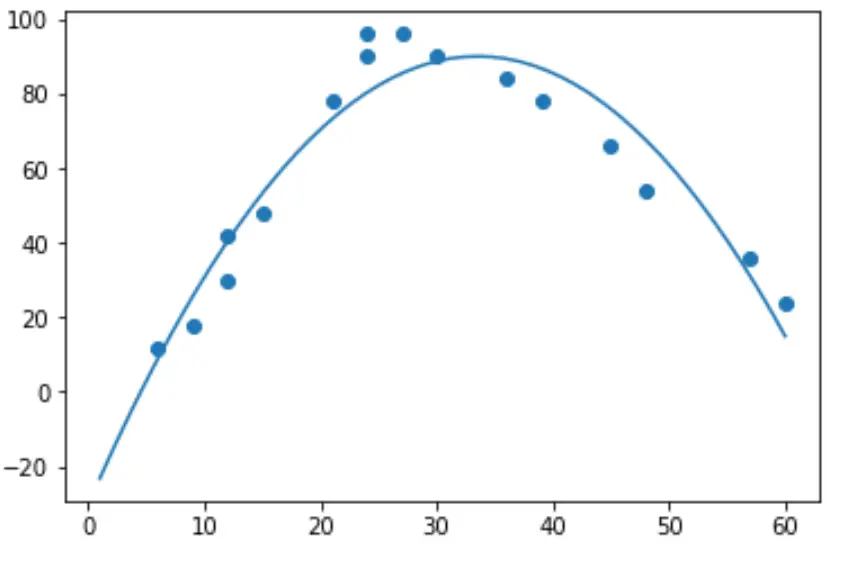
เราสามารถหาสมการถดถอยพหุนามพอดีได้โดยการพิมพ์ค่าสัมประสิทธิ์แบบจำลอง:

 print (model)

-0.107x 2 + 7.173x - 30.25

สมการถดถอยกำลังสองพอดีคือ:

ความสุข = -0.107(ชั่วโมง) ² + 7.173(ชั่วโมง) – 30.25

เราสามารถใช้สมการนี้เพื่อคำนวณระดับความสุขที่คาดหวังของแต่ละคนโดยพิจารณาจากชั่วโมงทำงานของพวกเขา ตัวอย่างเช่น ระดับความสุขที่คาดหวังของคนที่ทำงาน 30 ชั่วโมงต่อสัปดาห์คือ:

ความสุข = -0.107(30) ² + 7.173(30) – 30.25 = 88.64 .

นอกจากนี้เรายังสามารถเขียนฟังก์ชันสั้นๆ เพื่อให้ได้ค่า R-squared ของแบบจำลอง ซึ่งเป็นสัดส่วนของความแปรปรวนในตัวแปรตอบสนองที่สามารถอธิบายได้ด้วยตัวแปรทำนาย

 #define function to calculate r-squared
def polyfit(x, y, degree):
    results = {}
    coeffs = np.polyfit(x, y, degree)
    p = np.poly1d(coeffs)
    #calculate r-squared
    yhat = p(x)
    ybar = np.sum(y)/len(y)
    ssreg = np.sum((yhat-ybar)**2)
    sstot = np.sum((y - ybar)**2)
    results['r_squared'] = ssreg / sstot

    return results

#find r-squared of polynomial model with degree = 3
polyfit(hours, happ, 2)

{'r_squared': 0.9092114182131691}

ในตัวอย่างนี้ ค่า R ของโมเดลคือ 0.9092

ซึ่งหมายความว่า 90.92% ของความแปรผันของระดับความสุขที่รายงานสามารถอธิบายได้ด้วยตัวแปรทำนาย

แหล่งข้อมูลเพิ่มเติม

วิธีดำเนินการถดถอยพหุนามใน Python
วิธีดำเนินการถดถอยกำลังสองใน R
วิธีดำเนินการถดถอยกำลังสองใน Excel