วิธีดำเนินการแปลง box-cox ใน python

การแปลงแบบ box-cox เป็นวิธีการที่ใช้กันทั่วไปในการแปลงชุดข้อมูลที่ไม่กระจายแบบปกติให้เป็นชุด แบบกระจายแบบปกติ มากขึ้น

แนวคิดพื้นฐานเบื้องหลังวิธีนี้คือการหาค่าของ γ เพื่อให้ข้อมูลที่แปลงแล้วใกล้เคียงกับการแจกแจงแบบปกติมากที่สุด โดยใช้สูตรต่อไปนี้

• y(แลมบ์ดา) = (y ^แลม – 1) / แลม ถ้า y ≠ 0
• y(แลมบ์ดา) = log(y) ถ้า y = 0

เราสามารถทำการแปลง box-cox ใน Python ได้โดยใช้ฟังก์ชัน scipy.stats.boxcox()

ตัวอย่างต่อไปนี้แสดงวิธีใช้ฟังก์ชันนี้ในทางปฏิบัติ

ตัวอย่าง: การแปลง Box-Cox ใน Python

สมมติว่าเราสร้างชุดสุ่ม 1,000 ค่าจาก การแจกแจงแบบเอ็กซ์โปเนนเชียล :

 #load necessary packages
import numpy as np 
from scipy. stats import boxcox 
import seaborn as sns 

#make this example reproducible
n.p. random . seeds (0)

#generate dataset
data = np. random . exponential (size= 1000 )

#plot the distribution of data values
sns. distplot (data, hist= False , kde= True ) 

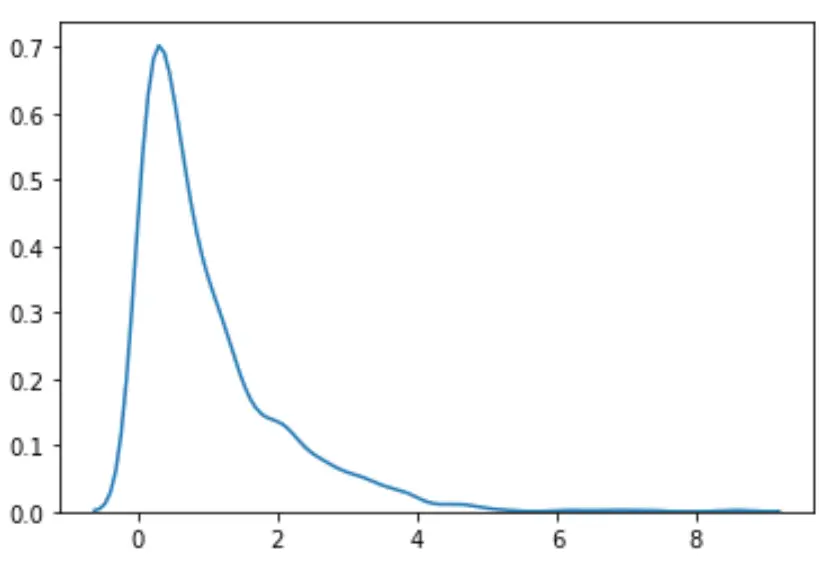
เราจะเห็นว่าการกระจายตัวดูไม่ปกติ

เราสามารถใช้ฟังก์ชัน boxcox() เพื่อค้นหาค่าที่เหมาะสมที่สุดของแลมบ์ดาซึ่งทำให้เกิดการแจกแจงแบบปกติมากขึ้น:

 #perform Box-Cox transformation on original data
transformed_data, best_lambda = boxcox(data) 

#plot the distribution of the transformed data values
sns. distplot (transformed_data, hist= False , kde= True ) 

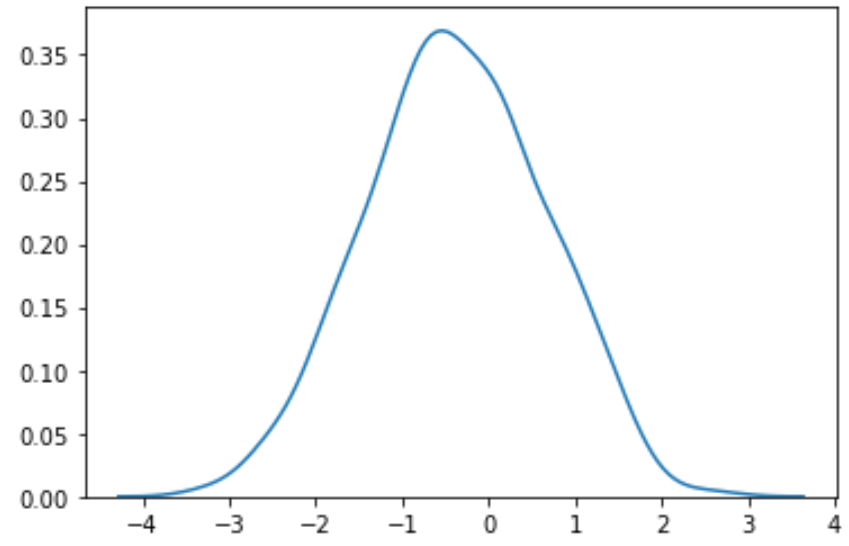
เราจะเห็นได้ว่าข้อมูลที่แปลงแล้วเป็นไปตามการแจกแจงแบบปกติมากกว่ามาก

นอกจากนี้เรายังสามารถค้นหาค่าแลมบ์ดาที่ใช้ในการแปลง Box-Cox ได้:

 #display optimal lambda value
print (best_lambda)

0.2420131978174143

แลมบ์ดาที่เหมาะสมที่สุดจะอยู่ที่ประมาณ 0.242

ดังนั้นค่าข้อมูลแต่ละค่าจึงถูกแปลงโดยใช้สมการต่อไปนี้:

ใหม่ = (เก่า ^0.242 – 1) / 0.242

เราสามารถยืนยันสิ่งนี้ได้โดยดูที่ค่าของข้อมูลต้นฉบับเทียบกับข้อมูลที่แปลงแล้ว:

 #view first five values of original dataset
data[0:5]

array([0.79587451, 1.25593076, 0.92322315, 0.78720115, 0.55104849])

#view first five values of transformed dataset
transformed_data[0:5]

array([-0.22212062, 0.23427768, -0.07911706, -0.23247555, -0.55495228])

ค่าแรกในชุดข้อมูลดั้งเดิมคือ 0.79587 ดังนั้นเราจึงใช้สูตรต่อไปนี้เพื่อแปลงค่านี้:

ใหม่ = (.79587 ^0.242 – 1) / 0.242 = -0.222

เราสามารถยืนยันได้ว่าค่าแรกในชุดข้อมูลที่แปลงแล้วคือ -0.222 จริงๆ

แหล่งข้อมูลเพิ่มเติม

วิธีสร้างและตีความพล็อต QQ ใน Python
วิธีทำการทดสอบความเป็นปกติของ Shapiro-Wilk ใน Python