อัตราข้อผิดพลาดในการจำแนกประเภทในการเรียนรู้ของเครื่อง: คำจำกัดความและตัวอย่าง

ในแมชชีนเลิร์นนิง อัตราการจัดหมวดหมู่ที่ไม่ถูกต้อง คือหน่วยเมตริกที่บอกเราถึงเปอร์เซ็นต์ของการสังเกตที่ แบบจำลองการจัดหมวดหมู่ คาดการณ์ไว้อย่างไม่ถูกต้อง

มีการคำนวณดังนี้:

อัตราการจัดหมวดหมู่ที่ไม่ถูกต้อง = # การคาดคะเนที่ไม่ถูกต้อง / # การคาดคะเนทั้งหมด

ค่าของอัตราการจำแนกประเภทที่ไม่ถูกต้องอาจแตกต่างกันตั้งแต่ 0 ถึง 1 โดยที่:

• 0 แสดงถึงแบบจำลองที่ไม่มีการคาดการณ์ที่ไม่ถูกต้อง
• 1 แสดงถึงแบบจำลองที่มีการทำนายที่ไม่ถูกต้องโดยสิ้นเชิง

ยิ่งค่าของอัตราการจำแนกประเภทต่ำเท่าใด โมเดลการจำแนกประเภทก็จะสามารถทำนายผลลัพธ์ของ ตัวแปรตอบสนอง ได้ดีขึ้นเท่านั้น

ตัวอย่างต่อไปนี้แสดงวิธีการคำนวณอัตราข้อผิดพลาดในการจัดประเภทสำหรับ แบบจำลองการถดถอยโลจิสติก ในทางปฏิบัติ

ตัวอย่าง: การคำนวณอัตราข้อผิดพลาดในการจำแนกประเภทสำหรับแบบจำลองการถดถอยลอจิสติก

สมมติว่าเราใช้แบบจำลองการถดถอยลอจิสติกส์เพื่อคาดการณ์ว่าผู้เล่นบาสเกตบอลระดับวิทยาลัยกว่า 400 คนจะถูกคัดเลือกเข้าสู่ NBA หรือไม่

เมทริกซ์ความสับสนต่อไปนี้สรุปการคาดการณ์ที่ทำโดยแบบจำลอง:

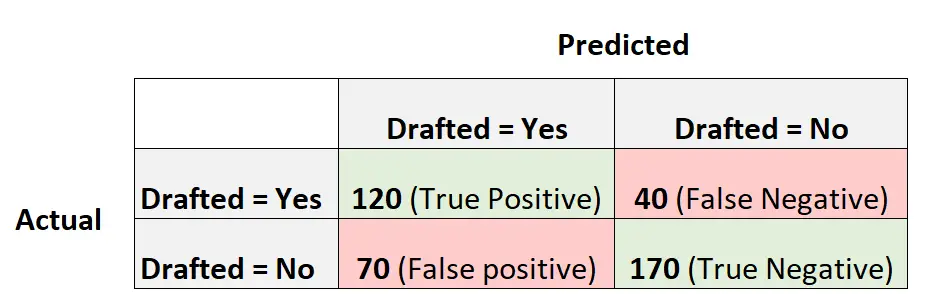
ต่อไปนี้เป็นวิธีการคำนวณอัตราข้อผิดพลาดในการจำแนกประเภทสำหรับแบบจำลอง:

• อัตราการจัดหมวดหมู่ที่ไม่ถูกต้อง = # การคาดคะเนที่ไม่ถูกต้อง / # การคาดคะเนทั้งหมด
• อัตราข้อผิดพลาดในการจำแนกประเภท = (ผลบวกลวง + ผลลบลวง) / (การคาดการณ์ทั้งหมด)
• อัตราการจำแนกประเภท = (70 + 40) / (400)
• อัตราการจำแนกประเภทที่ไม่ถูกต้อง = 0.275

อัตราข้อผิดพลาดในการจำแนกประเภทสำหรับรุ่นนี้คือ 0.275 หรือ 27.5%

ซึ่งหมายความว่าแบบจำลองทำนายผลลัพธ์ไม่ถูกต้องสำหรับผู้เล่น 27.5%

สิ่งที่ตรงกันข้ามกับอัตราข้อผิดพลาดในการจำแนกประเภทคือความแม่นยำ ซึ่งคำนวณได้ดังนี้

• ความแม่นยำ = 1 – อัตราข้อผิดพลาดในการจำแนกประเภท
• ความแม่นยำ = 1 – 0.275
• ความแม่นยำ = 0.725

ซึ่งหมายความว่าโมเดลทำนายผลลัพธ์ได้อย่างถูกต้องสำหรับผู้เล่น 72.5%

ข้อดีและข้อเสียของอัตราการจำแนกประเภทที่ไม่ถูกต้อง

อัตราการจำแนกประเภทให้ ประโยชน์ ดังต่อไปนี้:

• มันง่ายที่จะตีความ อัตราข้อผิดพลาดในการจำแนกประเภท 10% หมายความว่าแบบจำลองคาดการณ์ไม่ถูกต้อง 10% ของการสังเกตทั้งหมด
• มันง่ายที่จะคำนวณ อัตราการจำแนกประเภทที่ไม่ถูกต้องจะคำนวณจากจำนวนการคาดการณ์ที่ไม่ถูกต้องทั้งหมดหารด้วยจำนวนการคาดการณ์ทั้งหมด

อย่างไรก็ตาม อัตราข้อผิดพลาดในการจำแนกประเภทมี ข้อเสีย ดังนี้

• ซึ่งไม่ได้คำนึงถึงวิธีการกระจายข้อมูล ตัวอย่างเช่น สมมติว่า 90% ของผู้เล่นทั้งหมดไม่ได้ถูกดราฟต์เข้าสู่ NBA หากเรามีแบบจำลองที่คาดการณ์ง่ายๆ ว่าผู้เล่นทุกคนจะยังไม่ได้ร่าง โมเดลนั้นจะมีอัตราข้อผิดพลาดในการจำแนกประเภทเพียง 10% ดูเหมือนว่าจะต่ำ แต่จริงๆ แล้วโมเดลไม่สามารถคาดเดาผู้เล่นที่จะถูกดราฟท์ได้อย่างถูกต้อง

ในทางปฏิบัติ เรามักจะคำนวณอัตราข้อผิดพลาดในการจำแนกประเภทของโมเดลด้วยหน่วยวัดอื่นๆ เช่น:

• ความไว : “อัตราบวกที่แท้จริง” – เปอร์เซ็นต์ของผลลัพธ์เชิงบวกที่แบบจำลองสามารถตรวจจับได้
• ความจำเพาะ : “อัตราลบที่แท้จริง” – เปอร์เซ็นต์ของผลลัพธ์เชิงลบที่แบบจำลองสามารถตรวจจับได้
• คะแนน F1 : ตัวชี้วัด ที่บอกเราว่าแบบจำลองมีความแม่นยำเพียงใด โดยสัมพันธ์กับวิธีการกระจายข้อมูล

ด้วยการคำนวณค่าของแต่ละเมตริกเหล่านี้ เราจะเข้าใจได้อย่างถ่องแท้ว่าแบบจำลองสามารถคาดการณ์ได้ดีเพียงใด

แหล่งข้อมูลเพิ่มเติม

บทช่วยสอนต่อไปนี้ให้ข้อมูลเพิ่มเติมเกี่ยวกับแนวคิดการเรียนรู้ของเครื่องทั่วไป:

รู้เบื้องต้นเกี่ยวกับการถดถอยโลจิสติก
ความแม่นยำที่สมดุลคืออะไร?
คะแนน F1 เทียบกับความแม่นยำ: คุณควรใช้อันไหน