อัตราต่อรองที่ปรับปรุงแล้ว: คำจำกัดความ + ตัวอย่าง

ในสถิติ อัตราต่อรอง จะบอกเราถึงอัตราส่วนระหว่างความน่าจะเป็นของเหตุการณ์ที่เกิดขึ้นในกลุ่มการรักษา และความน่าจะเป็นของเหตุการณ์ที่เกิดขึ้นในกลุ่มควบคุม

อัตราส่วนราคาต่อรองมักปรากฏใน Logistic Regression ซึ่งเป็นวิธีการที่เราใช้เพื่อให้เหมาะกับโมเดลการถดถอยที่มีตัวแปรทำนายตั้งแต่ 1 ตัวขึ้นไปและตัวแปรตอบสนองแบบไบนารี

อัตราต่อรองที่ปรับแล้ว คืออัตราส่วนอัตราต่อรองที่ได้รับการปรับสำหรับตัวแปรทำนายอื่นๆ ในแบบจำลอง

มีประโยชน์อย่างยิ่งในการช่วยให้เราเข้าใจว่าตัวแปรทำนายส่งผลต่อโอกาสของเหตุการณ์ที่เกิดขึ้นอย่างไร หลังจาก ปรับผลกระทบของตัวแปรทำนายอื่นๆ แล้ว

ตัวอย่างต่อไปนี้แสดงให้เห็นถึงความแตกต่างระหว่างอัตราส่วนอัตราต่อรองและอัตราส่วนอัตราต่อรองที่ปรับปรุงแล้ว

ตัวอย่าง: การคำนวณอัตราส่วนอัตราต่อรองที่ปรับปรุงแล้ว

สมมติว่าเราต้องการเข้าใจว่าอายุของมารดาส่งผลต่อโอกาสที่จะมีทารกที่มีน้ำหนักแรกเกิดน้อยหรือไม่

ในการสำรวจสิ่งนี้ เราสามารถทำการถดถอยโลจิสติกโดยใช้อายุเป็นตัวแปรทำนายและน้ำหนักแรกเกิดต่ำ (ใช่หรือไม่ใช่) เป็น ตัวแปรตอบสนอง

สมมติว่าเรารวบรวมข้อมูลเกี่ยวกับมารดา 300 คนและพอดีกับแบบจำลองการถดถอยลอจิสติกส์ นี่คือผลลัพธ์:

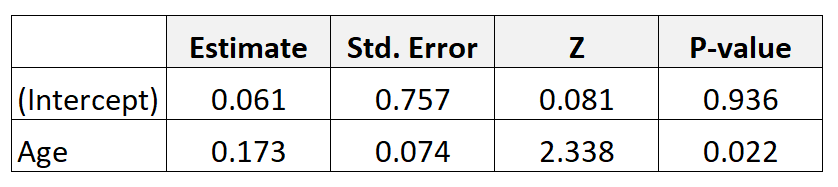
หากต้องการทราบอัตราต่อรองสำหรับอายุ เพียงยกกำลังการประมาณค่าสัมประสิทธิ์จากตาราง: e ^0.173 = 1.189

ข้อมูลนี้บอกเราว่าอายุที่เพิ่มขึ้นหนึ่งปีสัมพันธ์กับโอกาสที่ทารกจะมีน้ำหนักแรกเกิดต่ำเพิ่มขึ้น 1,189 ราย กล่าวอีกนัยหนึ่ง โอกาสในการมีลูกที่มีน้ำหนักแรกเกิดน้อยจะเพิ่มขึ้น 18.9% เมื่ออายุเพิ่มขึ้นทุกปี

อัตราส่วนอัตราต่อรองนี้เรียกว่าอัตราส่วนอัตราต่อรอง “ดิบ” หรืออัตราส่วนอัตราต่อรอง “ที่ไม่ได้ปรับปรุง” เนื่องจากไม่ได้ถูกปรับสำหรับตัวแปรทำนายอื่นๆ ในแบบจำลอง เนื่องจากเป็นตัวแปรทำนายเพียงตัวแปร เดียว ในแบบจำลอง

แต่สมมติว่าเราต้องการเข้าใจว่าอายุของมารดา และ นิสัยการสูบบุหรี่ส่งผลต่อโอกาสที่จะมีทารกที่มีน้ำหนักแรกเกิดน้อยหรือไม่

ในการสำรวจสิ่งนี้ เราสามารถทำการถดถอยโลจิสติกโดยใช้อายุและการสูบบุหรี่ (ใช่หรือไม่ใช่) เป็นตัวแปรทำนาย และน้ำหนักแรกเกิดต่ำเป็น ตัวแปรตอบสนอง

สมมติว่าเรารวบรวมข้อมูลเกี่ยวกับมารดา 300 คนและพอดีกับแบบจำลองการถดถอยลอจิสติกส์ นี่คือผลลัพธ์:

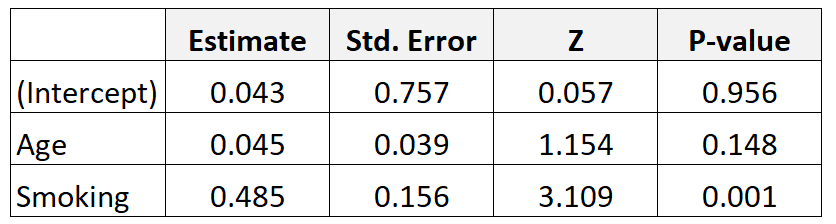
ต่อไปนี้เป็นวิธีการตีความผลลัพธ์:

อายุ: อัตราต่อรองที่ปรับตามอายุมีการคำนวณดังนี้: e ^0.045 = 1.046 ซึ่งหมายความว่าโอกาสในการมีลูกที่มีน้ำหนักแรกเกิดน้อยจะเพิ่มขึ้น 4.6% สำหรับอายุที่เพิ่มขึ้นทุกปี โดยสมมติว่าตัวแปร การสูบบุหรี่ ยังคงที่

ตัวอย่างเช่น สมมติว่าแม่ A และแม่ B สูบบุหรี่ทั้งคู่ ถ้าแม่ A มีอายุมากกว่าแม่ B หนึ่งปี ความน่าจะเป็นที่แม่ A จะมีทารกน้ำหนักแรกเกิดน้อยคือ 1.046 เท่าของความน่าจะเป็นที่แม่ B จะมีทารกน้ำหนักแรกเกิดน้อย

การสูบบุหรี่ : อัตราต่อรองที่ปรับแล้วสำหรับการสูบบุหรี่มีการคำนวณดังนี้: ^e.485 = 1.624 ซึ่งหมายความว่าโอกาสในการมีลูกที่มีน้ำหนักแรกเกิดน้อยจะเพิ่มขึ้นถึง 62.4% หากแม่สูบบุหรี่ (เทียบกับไม่สูบบุหรี่) โดยถือว่าตัวแปร อายุ คงที่

ตัวอย่างเช่น สมมติว่าแม่ A และแม่ B มีอายุ 30 ปีทั้งคู่ หากแม่ A สูบบุหรี่ในระหว่างตั้งครรภ์และแม่ B ไม่สูบบุหรี่ โอกาสที่แม่ A จะมีลูกน้ำหนักแรกเกิดน้อยจะสูงกว่าโอกาสที่แม่ B จะมีลูกน้ำหนักแรกเกิดน้อยถึง 62.4%

โปรดทราบว่าอัตราส่วนอัตราต่อรองที่ปรับตามอายุจะต่ำกว่าอัตราส่วนอัตราต่อรองที่ยังไม่ได้ปรับปรุงจากตัวอย่างก่อนหน้านี้ เนื่องจากเมื่อตัวแปรทำนายอื่นๆ เพิ่มโอกาสที่ตัวแปรตอบสนองจะเกิดขึ้น อัตราต่อรองที่ปรับแล้วสำหรับตัวแปรทำนายที่มีอยู่แล้วในแบบจำลองจะลดลงเสมอ

สรุป: อัตราต่อรองเทียบกับอัตราส่วนอัตราต่อรองที่ปรับปรุงแล้ว

อัตราส่วนอัตราต่อรอง (บางครั้งเรียกว่าอัตราส่วนอัตราต่อรอง “ดิบ”) มีประโยชน์ในการบอกเราว่าการเปลี่ยนแปลงในตัวแปรทำนายส่งผลต่อโอกาสที่ตัวแปรตอบสนองจะเกิดขึ้นอย่างไร

อัตราต่อรองที่ปรับแล้ว มีประโยชน์ในการบอกเราว่าการเปลี่ยนแปลงในตัวแปรทำนายส่งผลต่อโอกาสที่ตัวแปรตอบสนองจะเกิดขึ้นอย่างไร หลังจาก ควบคุมตัวแปรทำนายอื่นๆ ในแบบจำลองแล้ว

แหล่งข้อมูลเพิ่มเติม

รู้เบื้องต้นเกี่ยวกับการถดถอยโลจิสติก
วิธีดำเนินการถดถอยโลจิสติกใน R
วิธีการดำเนินการถดถอยโลจิสติกใน Python