วิธีใช้ฟังก์ชัน logest ใน google ชีต (พร้อมตัวอย่าง)
คุณสามารถใช้ฟังก์ชัน LOGEST ใน Google ชีตเพื่อคำนวณสูตรสำหรับเส้นโค้งเอ็กซ์โปเนนเชียลที่เหมาะกับข้อมูลของคุณ
สมการของเส้นโค้งจะอยู่ในรูปแบบต่อไปนี้:
y = b* มx
ฟังก์ชันนี้ใช้ไวยากรณ์พื้นฐานต่อไปนี้:
= LOGEST ( known_data_y, [known_data_x], [b], [verbose] )
ทอง:
- known_data_y : อาร์เรย์ของค่า y ที่ทราบ
- known_data_x : อาร์เรย์ของค่า x ที่ทราบ
- b : อาร์กิวเมนต์ทางเลือก ถ้าเป็น TRUE ค่าคงที่ b จะถูกประมวลผลตามปกติ ถ้าเป็น FALSE ค่าคงที่ b จะถูกตั้งค่าเป็น 1
- verbose : อาร์กิวเมนต์ที่เป็นทางเลือก ถ้าเป็น TRUE สถิติการถดถอยเพิ่มเติมจะถูกส่งกลับ หากเป็น FALSE ระบบจะไม่ส่งคืนสถิติการถดถอยเพิ่มเติม
ตัวอย่างทีละขั้นตอนต่อไปนี้แสดงวิธีใช้ฟังก์ชันนี้ในทางปฏิบัติ
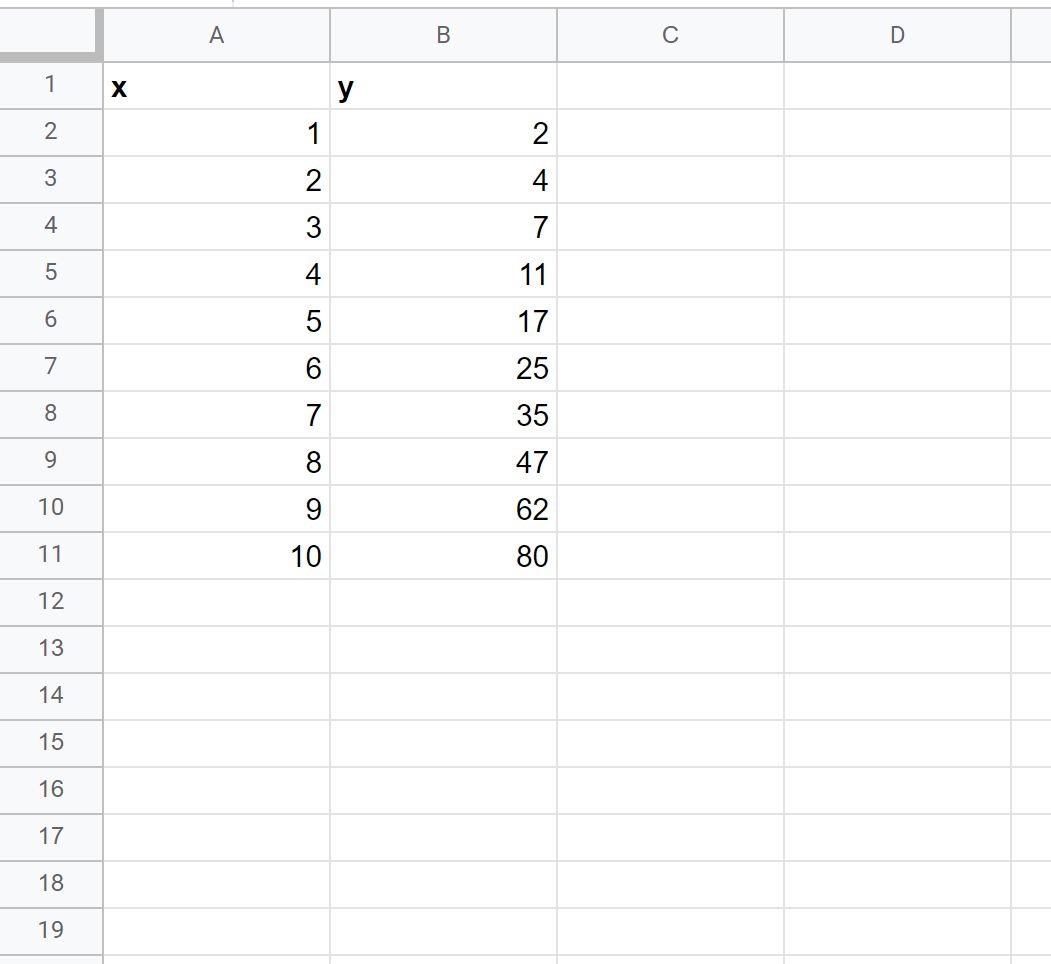
ขั้นตอนที่ 1: ป้อนข้อมูล
ขั้นแรก ให้ป้อนข้อมูลชุดต่อไปนี้ลงใน Google ชีต:
ขั้นตอนที่ 2: แสดงภาพข้อมูล
ต่อไป เรามาสร้างแผนภูมิกระจายอย่างรวดเร็วของ x เทียบกับ y เพื่อตรวจสอบว่าข้อมูลเป็นไปตามเส้นโค้งเอ็กซ์โพเนนเชียลจริง:
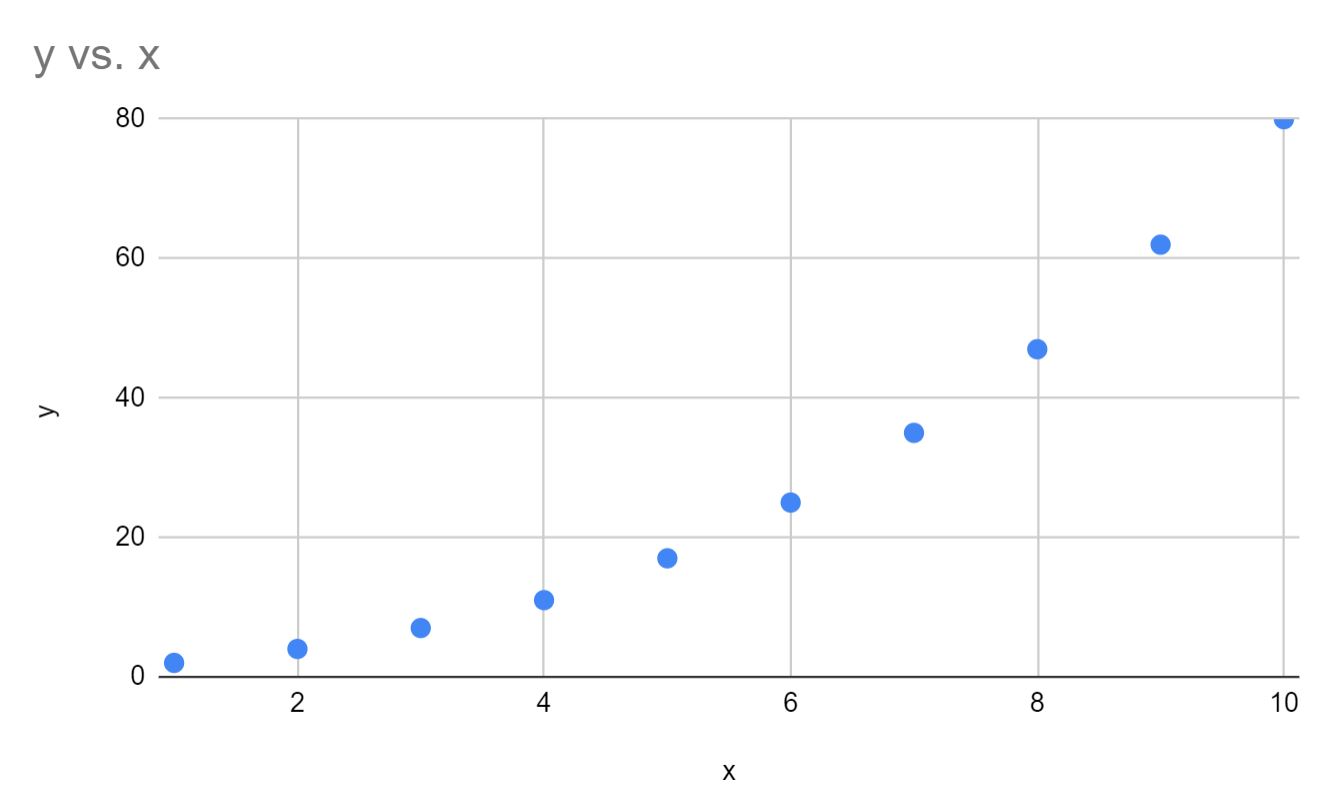
เราจะเห็นได้ว่าข้อมูลเป็นไปตามเส้นโค้งเอ็กซ์โพเนนเชียลจริงๆ
ขั้นตอนที่ 3: ใช้ LOGEST เพื่อค้นหาสูตรสำหรับเส้นโค้งเอ็กซ์โปเนนเชียล
จากนั้นเราสามารถพิมพ์สูตรต่อไปนี้ในเซลล์ใดก็ได้เพื่อคำนวณสูตรเส้นโค้งเอ็กซ์โปเนนเชียล:
=LOGEST( B2:B11 , A2:A11 )
ภาพหน้าจอต่อไปนี้แสดงวิธีใช้สูตรนี้ในทางปฏิบัติ:
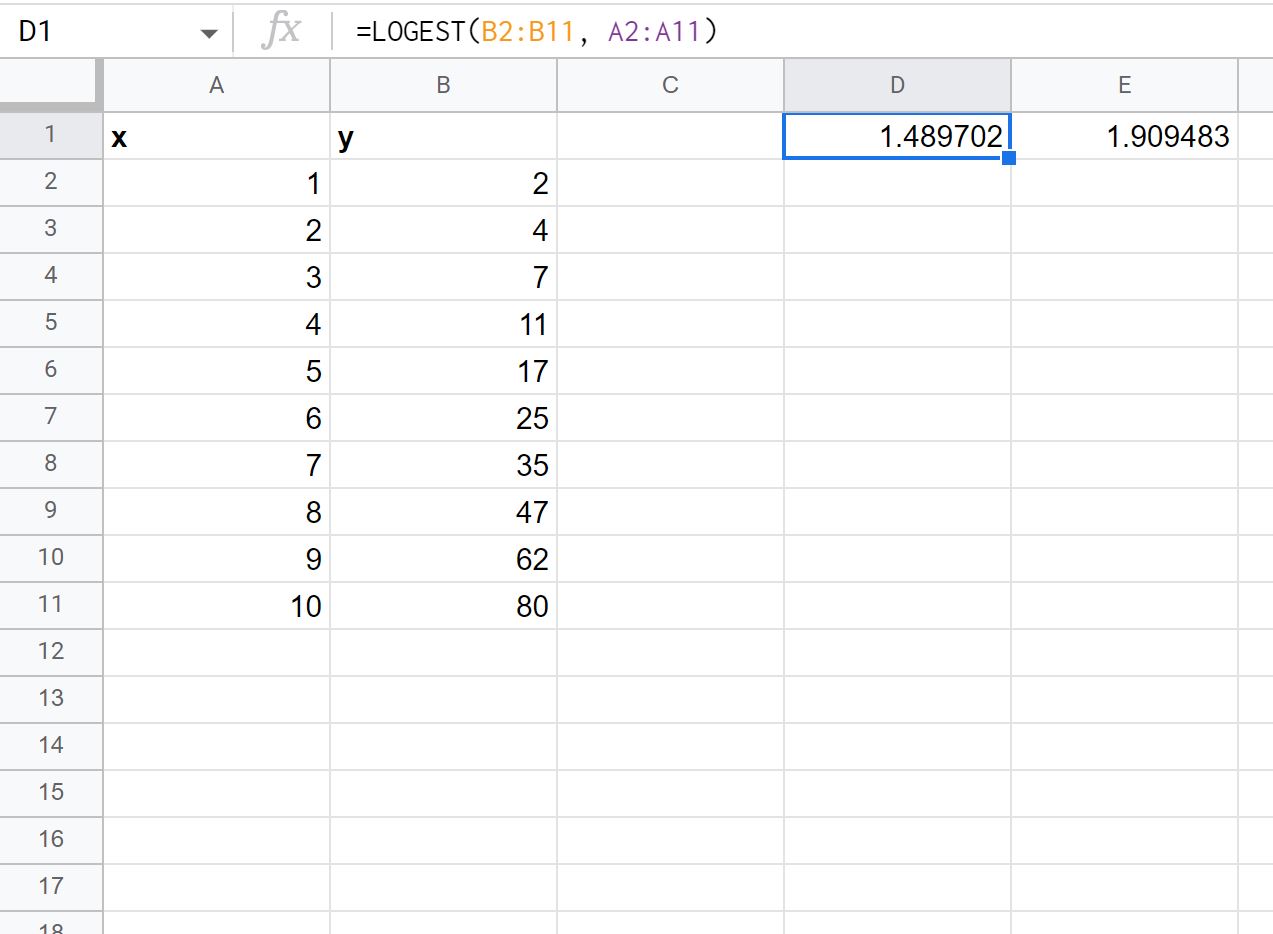
ค่าแรกของผลลัพธ์แสดงถึงค่าของ m และค่าที่สองของผลลัพธ์แสดงถึงค่าของ b ในสมการ:
y = b* มx
ดังนั้น เราจะเขียนสูตรเส้นโค้งเอ็กซ์โปเนนเชียลได้ดังนี้
y = 1.909483 * 1.489702x
จากนั้นเราสามารถใช้สูตรนี้เพื่อทำนายค่า y ตามค่าของ x
ตัวอย่างเช่น ถ้า xa มีค่าเป็น 8 เราก็คาดการณ์ว่า y มีค่าเป็น 46.31 :
y = 1.909483 * 1.489702 8 = 46.31
ขั้นตอนที่ 4 (ไม่บังคับ): ดูสถิติการถดถอยเพิ่มเติม
เราสามารถตั้งค่าอาร์กิวเมนต์ โดยละเอียด ในฟังก์ชัน LOGEST ให้เท่ากับ TRUE เพื่อแสดงสถิติการถดถอยเพิ่มเติมสำหรับสมการถดถอยที่ติดตั้ง:
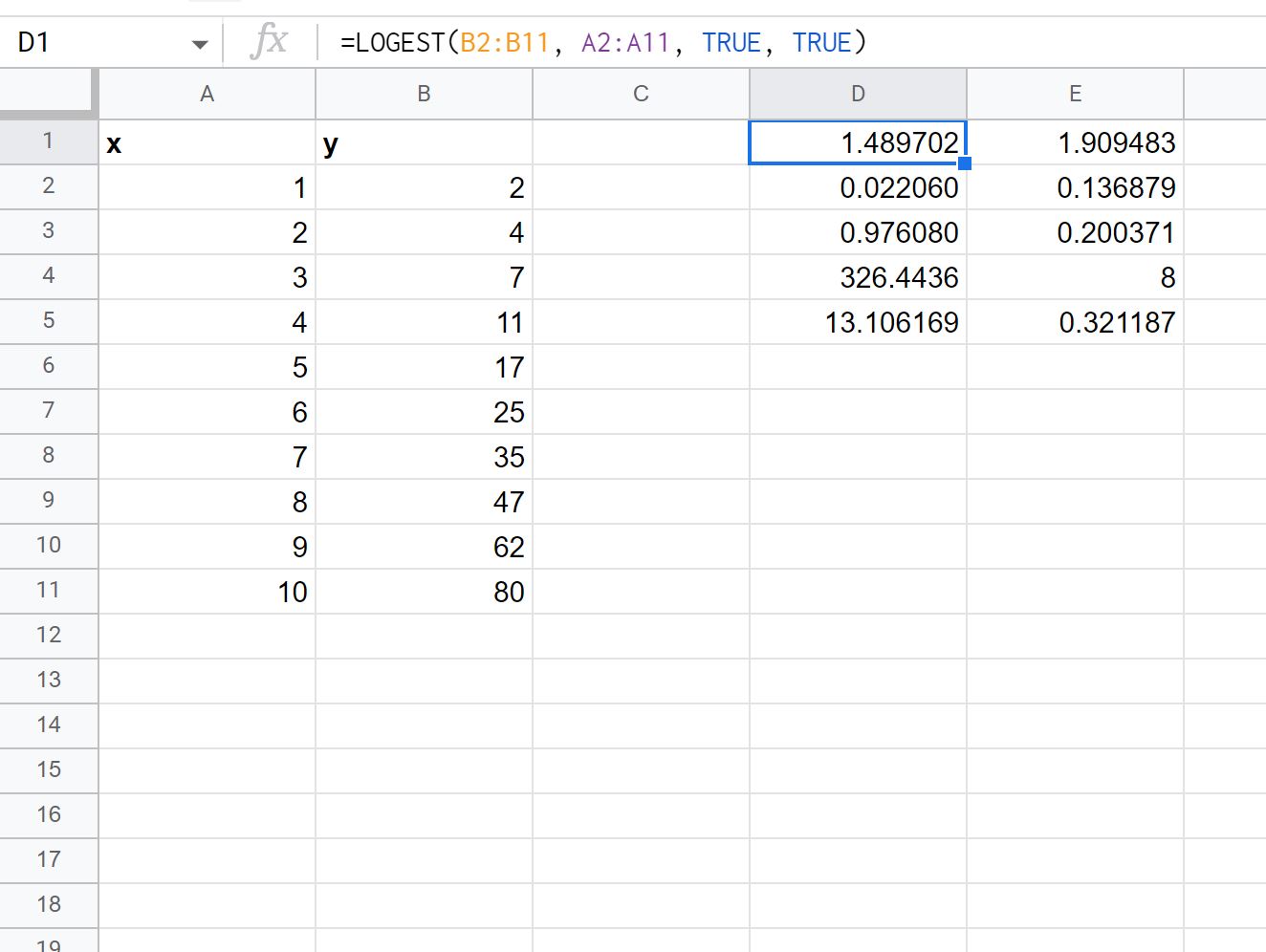
ต่อไปนี้เป็นวิธีตีความแต่ละค่าในผลลัพธ์:
- ข้อผิดพลาดมาตรฐานสำหรับ m คือ 0.02206
- ข้อผิดพลาดมาตรฐานสำหรับ b คือ 0.136879
- R 2 ของรุ่นคือ .97608 .
- ข้อผิดพลาดมาตรฐานสำหรับ y คือ . 200371
- สถิติ F คือ 326.4436
- องศาอิสระคือ 8
- ผลรวมการถดถอยของกำลังสองคือ 13.106169
- ผลรวมที่เหลือของกำลังสองคือ .321187 .
โดยทั่วไป การวัดที่น่าสนใจที่สุดในสถิติเพิ่มเติมเหล่านี้คือค่า R 2 ซึ่งแสดงถึงสัดส่วนของความแปรปรวนในตัวแปรตอบสนองที่สามารถอธิบายได้ด้วยตัวแปรทำนาย
ค่าของ R 2 สามารถเปลี่ยนแปลงได้ตั้งแต่ 0 ถึง 1
เนื่องจาก R 2 ของโมเดลนี้ใกล้กับ 1 จึงบอกเราว่าตัวแปรทำนาย x ทำนายค่าของตัวแปรตอบสนอง y ได้ดี
ที่เกี่ยวข้อง: ค่า R-squared ที่ดีคืออะไร?
แหล่งข้อมูลเพิ่มเติม
บทช่วยสอนต่อไปนี้จะอธิบายวิธีทำสิ่งทั่วไปอื่นๆ ใน Google ชีต:
วิธีดำเนินการถดถอยเชิงเส้นใน Google ชีต
วิธีดำเนินการถดถอยพหุนามใน Google ชีต
วิธีคำนวณ R-squared ใน Google ชีต