Tau ของ kendall: คำจำกัดความ + ตัวอย่าง

ในทางสถิติ ความสัมพันธ์ หมายถึงจุดแข็งและทิศทางของความสัมพันธ์ระหว่างตัวแปรสองตัว ค่าของสัมประสิทธิ์สหสัมพันธ์สามารถอยู่ในช่วงตั้งแต่ -1 ถึง 1 โดย -1 หมายถึงความสัมพันธ์เชิงลบที่สมบูรณ์แบบ 0 หมายถึงไม่มีความสัมพันธ์ และ 1 หมายถึงความสัมพันธ์เชิงบวกที่สมบูรณ์แบบ

ค่าสัมประสิทธิ์สหสัมพันธ์ที่ใช้กันมากที่สุดคือ ค่าสัมประสิทธิ์สหสัมพันธ์แบบเพียร์สัน ซึ่งวัดความสัมพันธ์เชิงเส้นระหว่างตัวแปรตัวเลขสองตัว

ค่าสัมประสิทธิ์สหสัมพันธ์ที่ใช้กันน้อยกว่าคือ Kendall’s Tau ซึ่งวัดความสัมพันธ์ระหว่างสองคอลัมน์ของข้อมูลที่จัดอันดับ

สูตรการคำนวณ Tau ของ Kendall ซึ่งมักใช้ตัวย่อ τ มีดังต่อไปนี้:

τ = (ซีดี) / (C+D)

ทอง:

C = จำนวนคู่ที่ตรงกัน

D = จำนวนคู่ที่ไม่ลงรอยกัน

ตัวอย่างต่อไปนี้แสดงวิธีใช้สูตรนี้ในการคำนวณค่าสัมประสิทธิ์สหสัมพันธ์อันดับ Tau ของ Kendall สำหรับข้อมูลอันดับสองคอลัมน์

ตัวอย่างการคำนวณ Tau ของ Kendall

สมมติว่าโค้ชบาสเกตบอลสองคนมีผู้เล่นอยู่ในอันดับ 12 จากแย่ที่สุดไปหาดีที่สุด ตารางต่อไปนี้แสดงอันดับโค้ชแต่ละคนที่มอบหมายให้กับผู้เล่น:

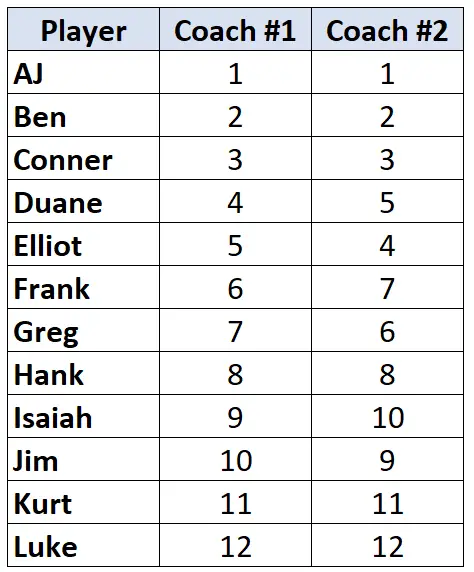
เนื่องจากเรากำลังทำงานกับข้อมูลจัดอันดับสองคอลัมน์ จึงเหมาะสมที่จะใช้ Tau ของ Kendall เพื่อคำนวณความสัมพันธ์ระหว่างการจัดอันดับของโค้ชทั้งสอง ทำตามขั้นตอนต่อไปนี้เพื่อคำนวณ Tau ของ Kendall:

ขั้นตอนที่ 1: นับจำนวนคู่ที่ตรงกัน

ดูเฉพาะอันดับโค้ช #2 เท่านั้น เริ่มจากผู้เล่นคนแรก นับว่ามีอันดับต่ำกว่าเขา สูง กว่ากี่อันดับ ตัวอย่างเช่น มีตัวเลข 11 ตัวที่อยู่ใต้ “1” ซึ่งใหญ่กว่า ดังนั้นเราจะเขียน 11:

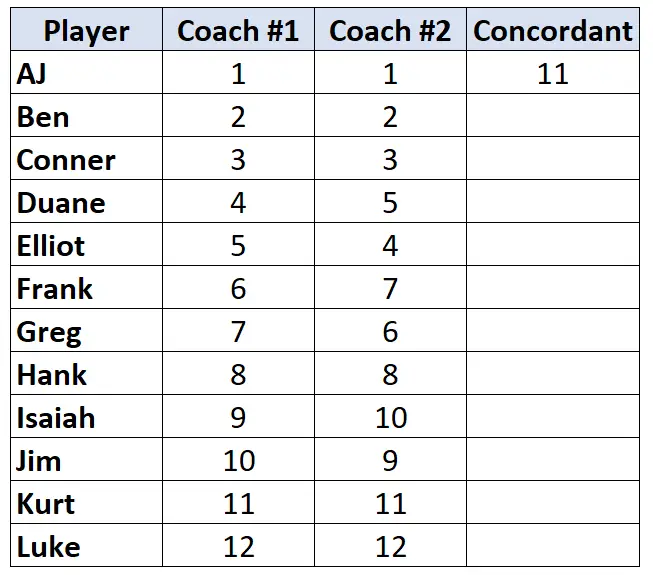
ย้ายไปยังผู้เล่นคนถัดไปและทำซ้ำขั้นตอนนี้ มีตัวเลข 10 ตัวที่อยู่ใต้ “2” ซึ่งใหญ่กว่า ดังนั้นเราจะเขียนเป็น 10:

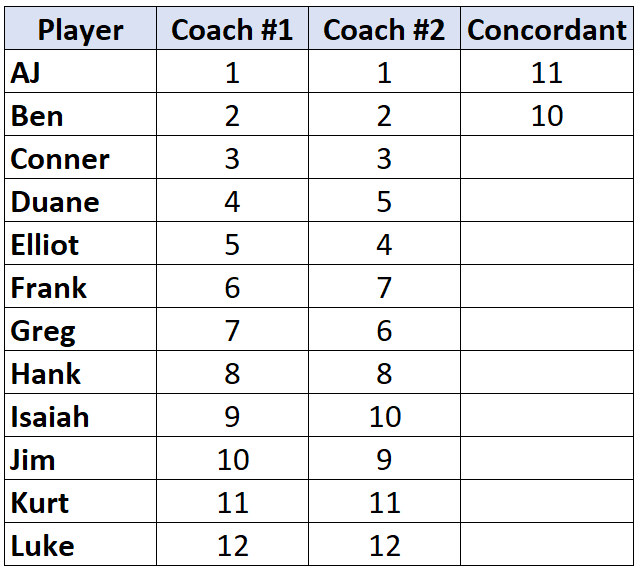
เมื่อเราเข้าถึงผู้เล่นที่มีอันดับ ต่ำกว่า ผู้เล่นก่อนหน้าเขา เขาจะได้รับการกำหนดค่าเดียวกันกับผู้เล่นก่อนหน้าเขา ตัวอย่างเช่น เอลเลียตมีอันดับ “4” ซึ่งต่ำกว่าอันดับ “5” ของผู้เล่นคนก่อน ดังนั้นเขาจึงได้รับมอบหมายให้มีค่าเดียวกันกับผู้เล่นก่อนหน้าเขา:

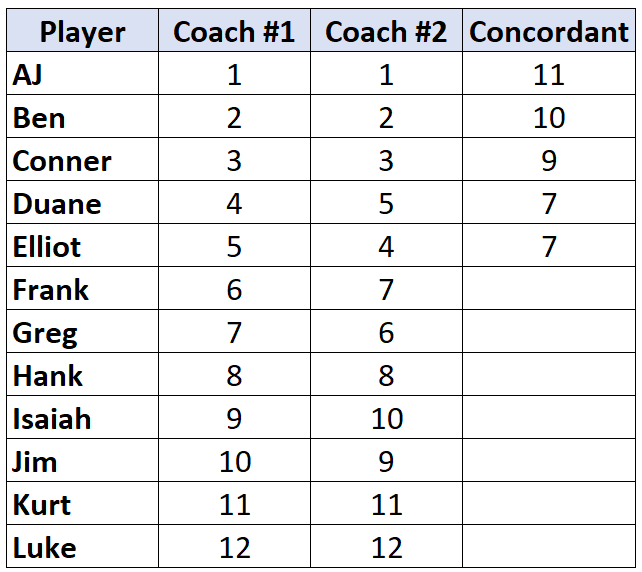
ทำซ้ำขั้นตอนนี้กับผู้เล่นทุกคน:

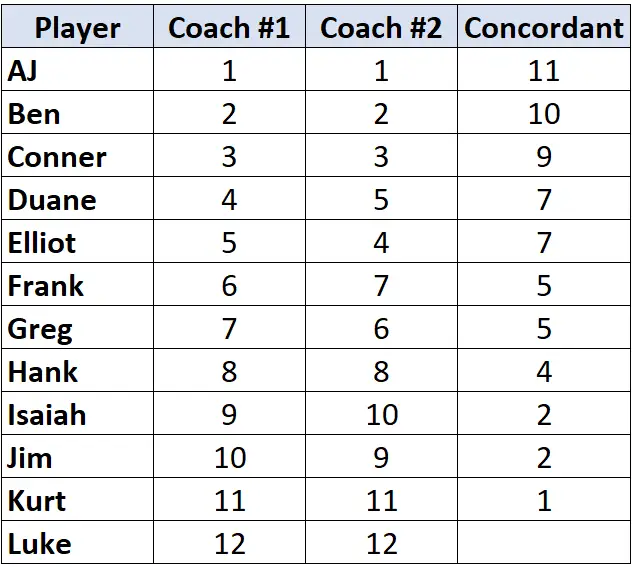
ขั้นตอนที่ 2: นับจำนวนคู่ที่ไม่ลงรอยกัน

ดูเฉพาะอันดับของ Coach #2 เท่านั้น สำหรับผู้เล่นแต่ละคน ให้นับว่ามีอันดับต่ำกว่าเขาหรือเธอที่ เล็กกว่ากี่อันดับ ตัวอย่างเช่น โค้ชหมายเลข 2 กำหนดให้ AJ อยู่ในอันดับ “1” และไม่มีผู้เล่นคนใดที่ต่ำกว่าเขามีอันดับต่ำกว่า ดังนั้นเราจึงกำหนดค่าเป็น 0:

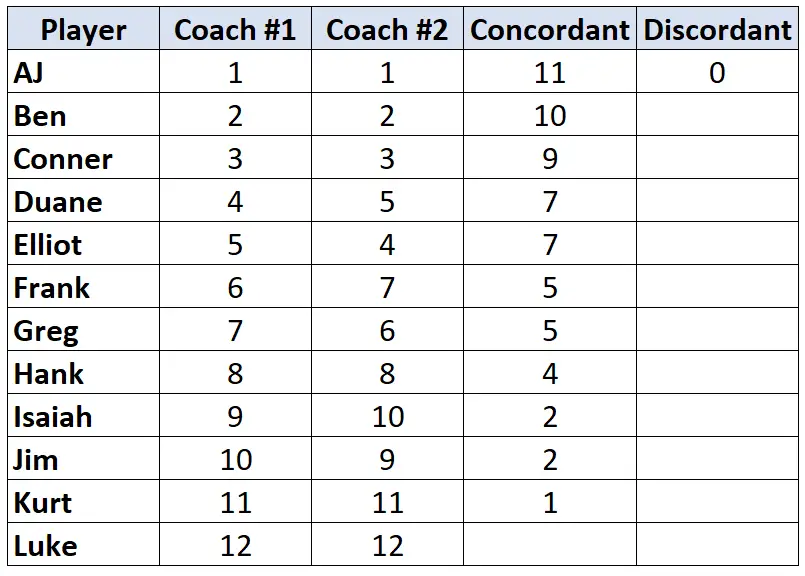
ทำซ้ำขั้นตอนนี้สำหรับผู้เล่นแต่ละคน:

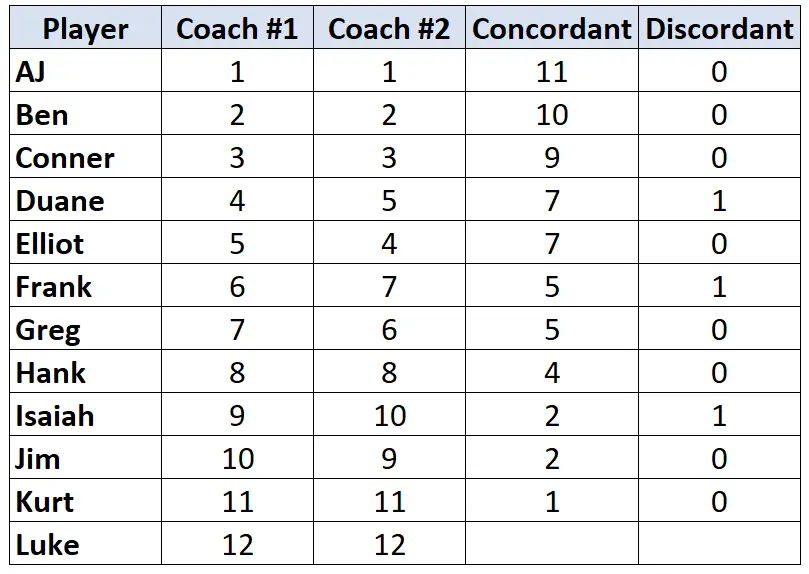
ขั้นตอนที่ 3: คำนวณผลรวมของแต่ละคอลัมน์แล้วหา Tau ของ Kendall

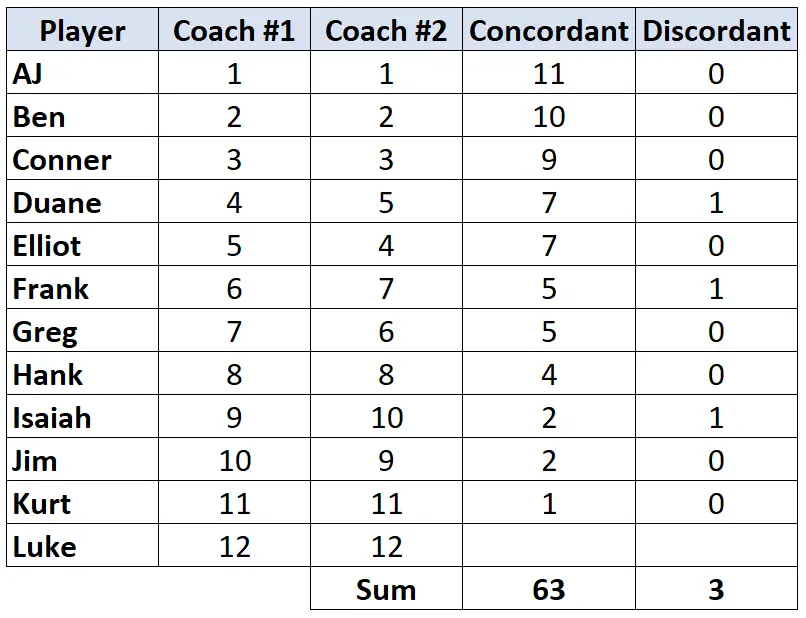
เทาของเคนดัลล์ = (CD) / (C+D) = (63-3) / (63+3) = (60/66) = 0.909

ความสำคัญทางสถิติของเทาว์ของเคนดัลล์

เมื่อคุณมีมากกว่า n=10 คู่ โดยทั่วไป Tau ของ Kendall จะเป็นไปตามการแจกแจงแบบปกติ คุณสามารถใช้สูตรต่อไปนี้เพื่อคำนวณคะแนน z สำหรับ Tau ของ Kendall:

z = 3τ*√ n(n-1) / √ 2(2n+5)

ทอง:

τ = ค่าที่คุณคำนวณสำหรับ Tau ของ Kendall

n = จำนวนคู่

ต่อไปนี้เป็นวิธีคำนวณ z สำหรับตัวอย่างก่อนหน้านี้:

z = 3(.909)*√ 12(12-1) / √ 2(2*12+5) = 4.11 .

เมื่อใช้เครื่องคำนวณคะแนน Z ค่า P เราจะเห็นว่าค่า p สำหรับคะแนน z นี้คือ 0.00004 ซึ่งมีนัยสำคัญทางสถิติที่ระดับอัลฟ่า 0.05 ดังนั้นจึงมีความสัมพันธ์ที่มีนัยสำคัญทางสถิติระหว่างอันดับที่โค้ชทั้งสองมอบหมายให้กับผู้เล่น

โบนัส: วิธีคำนวณ Tau ของ Kendall ใน R

ในซอฟต์แวร์สถิติ R คุณสามารถใช้ฟังก์ชัน kendall.tau() จากไลบรารี VGAM เพื่อคำนวณ Tau ของ Kendall สำหรับเวกเตอร์สองตัว ซึ่งใช้ไวยากรณ์ต่อไปนี้:

kendall.tau(x, y)

โดยที่ x และ y เป็นเวกเตอร์ดิจิทัลสองตัวที่มีความยาวเท่ากัน

รหัสต่อไปนี้แสดงวิธีคำนวณ Tau ของ Kendall สำหรับข้อมูลที่เราใช้ในตัวอย่างก่อนหน้านี้:

 #load VGAM
library(VGAM)

#create vector for each coach's rankings
coach_1 <- c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12)
coach_2 <- c(1, 2, 3, 5, 4, 7, 6, 8, 10, 9, 11, 12)

#calculate Kendall's Tau
kendall.tau(coach_1, coach_2)

#[1] 0.9090909

สังเกตว่าค่า Tau ของ Kendall ตรงกับค่าที่เราคำนวณด้วยตนเองอย่างไร