ตัวแปรเชิงหมวดหมู่หรือเชิงปริมาณ: คำจำกัดความ + ตัวอย่าง

ในสถิติ ตัวแปรสามารถจำแนกได้เป็น ประเภท หรือ เชิงปริมาณ

ตัวแปรหมวดหมู่: ตัวแปรที่ใช้ชื่อหรือป้ายกำกับ ตัวอย่างได้แก่:

• สถานภาพการสมรส (“แต่งงานแล้ว” “โสด” “หย่าร้าง”)
• สถานะการสูบบุหรี่ (“ผู้สูบบุหรี่”, “ผู้ไม่สูบบุหรี่”)
• สีตา (“น้ำเงิน”, “เขียว”, “เฮเซล”)
• ระดับการศึกษา (เช่น “มัธยมปลาย” “ปริญญาตรี” “ปริญญาโท”)

ตัวแปรเชิงปริมาณ: ตัวแปรที่รับค่าตัวเลข ตัวอย่างได้แก่:

• ขนาดของแต่ละบุคคล
• ขนาดประชากรของเมือง
• จำนวนนักเรียนในชั้นเรียน
• จำนวนตารางฟุตในบ้าน

ตารางต่อไปนี้สรุปความแตกต่างระหว่างตัวแปรทั้งสองประเภทนี้:

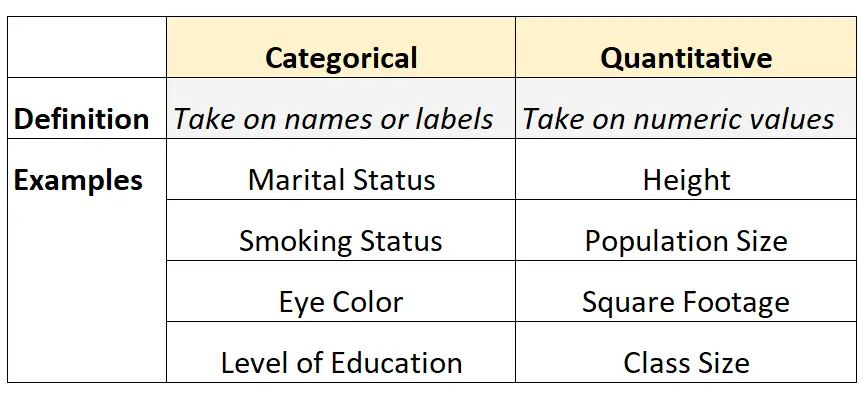
ตัวอย่าง: ตัวแปรเด็ดขาดและตัวแปรเชิงปริมาณ

ใช้ตัวอย่างต่อไปนี้เพื่อทำความเข้าใจตัวแปรเชิงหมวดหมู่และเชิงปริมาณให้ดียิ่งขึ้น

ตัวอย่างที่ 1: ความสูงของพืช

นักพฤกษศาสตร์เดินผ่านป่าในท้องถิ่นและวัดความสูงของพืชบางชนิด ตัวแปร ความสูงของพืช เป็น ตัวแปรเชิงปริมาณ เนื่องจากใช้ค่าตัวเลข ตัวอย่างเช่น ความสูงอาจเป็น 15 นิ้ว, 17.5 นิ้ว, 19.2 นิ้ว เป็นต้น

ตัวอย่างที่ 2: ที่พักให้เช่า

นักวิจัยสัมภาษณ์ผู้คน 200 คนและถามพวกเขาว่าสถานที่พักผ่อนที่พวกเขาชื่นชอบคือที่ไหน ตัวแปร สถานที่พักร้อน เป็น ตัวแปรเชิงหมวดหมู่ เนื่องจากต้องใช้ชื่อ ตัวอย่างเช่น คำตอบอาจรวมถึง “ไมอามี่”, “ซานฟรานซิสโก”, “ฮิลตัน เฮด” เป็นต้น

ตัวอย่างที่ 3: พรรคการเมือง

นักรัฐศาสตร์สัมภาษณ์คน 50 คนในเมืองหนึ่ง และถามพวกเขาว่าพวกเขาระบุตัวตนด้วยพรรคการเมืองใด ตัวแปร พรรคการเมือง เป็น ตัวแปรเชิงหมวดหมู่ เนื่องจากมีป้ายกำกับ ตัวอย่างเช่น คำตอบอาจรวมถึง “พรรคเดโมแครต” “พรรครีพับลิกัน” “อิสระ” เป็นต้น

ตัวอย่างที่ 4: เวลาดำเนินการ

โค้ชบันทึกเวลาการแข่งขันของผู้ติดตาม 20 คนของเขา ตัวแปร เวลาปฏิบัติงาน เป็น ตัวแปรเชิงปริมาณ เนื่องจากใช้ค่าตัวเลข ตัวอย่างเช่น รันไทม์อาจเป็น 58 วินาที, 60.343 วินาที, 65.4 วินาที เป็นต้น

ตัวอย่างที่ 5: ราคาที่อยู่อาศัย

นักเศรษฐศาสตร์รวบรวมข้อมูลเกี่ยวกับราคาที่อยู่อาศัยในเมืองหนึ่งๆ ตัวแปร ราคาทรัพย์สิน เป็น ตัวแปรเชิงปริมาณ เนื่องจากใช้ค่าตัวเลข ตัวอย่างเช่น ราคาบ้านอาจเป็น $149,000, $289,000, $560,000 เป็นต้น

วิธีอธิบายตัวแปรเชิงหมวดหมู่และเชิงปริมาณ

เราสามารถสรุป ตัวแปรหมวดหมู่ได้ โดยใช้ตารางความถี่

ตัวอย่างเช่น สมมติว่าเรารวบรวมข้อมูลสีตาของบุคคล 100 คน เนื่องจาก “สีตา” เป็นตัวแปรเชิงหมวดหมู่ เราจึงสามารถใช้ตารางความถี่ต่อไปนี้เพื่อสรุปค่าต่างๆ ได้:

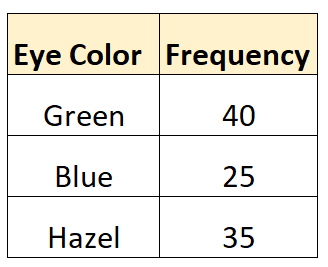
เราสามารถสรุป ตัวแปรเชิงปริมาณ โดยใช้สถิติเชิงพรรณนาต่างๆ

ตัวอย่างเช่น สมมติว่าเรารวบรวมข้อมูลบนพื้นที่เป็นตารางฟุตของบ้าน 100 หลัง เนื่องจาก “พื้นที่เป็นตารางฟุต” เป็นตัวแปรเชิงปริมาณ เราจึงสามารถใช้สถิติเชิงพรรณนาต่อไปนี้เพื่อสรุปค่าต่างๆ ได้:

• เฉลี่ย: 1,800
• มัธยฐาน: 2,150
• โหมด: 1600
• ระยะ: 6,500
• สเกลระหว่างควอไทล์: 890
• ส่วนเบี่ยงเบนมาตรฐาน: 235

ตัวชี้วัดเหล่านี้ช่วยให้เราทราบว่า ค่ากลาง อยู่ที่ใดรวมถึงการแจกแจงค่าสำหรับตัวแปรนั้น

ที่เกี่ยวข้อง: วิธีการพล็อตข้อมูลหมวดหมู่ใน R