วิธีเปรียบเทียบฮิสโตแกรม (พร้อมตัวอย่าง)
ฮิสโตแกรม เป็นแผนภูมิประเภทหนึ่งที่ช่วยให้เราเห็นการกระจายของค่าในชุดข้อมูล
แกน X แสดงค่าของชุดข้อมูล และแกน Y แสดงความถี่ของแต่ละค่า
ฮิสโตแกรมมีประโยชน์เพราะช่วยให้เราเข้าใจการกระจายของค่าในชุดข้อมูลได้อย่างรวดเร็ว นอกจากนี้ยังมีประโยชน์สำหรับการเปรียบเทียบชุดข้อมูลสองชุดที่แตกต่างกันอีกด้วย
เมื่อเปรียบเทียบฮิสโตแกรมตั้งแต่สองตัวขึ้นไป เราสามารถตอบคำถามที่แตกต่างกันได้สามข้อ:
1. ค่ามัธยฐานเปรียบเทียบกันอย่างไร?
เราสามารถประมาณค่ามัธยฐานได้คร่าวๆ ว่าค่ามัธยฐานอยู่ใกล้กึ่งกลางของแต่ละฮิสโตแกรม ทำให้เราสามารถเปรียบเทียบค่ามัธยฐานของการแจกแจงได้
2. การกระจายตัวเปรียบเทียบกันอย่างไร?
เราสามารถมองเห็นได้ด้วยตาเปล่าว่าฮิสโตแกรมใดที่มีการกระจายมากกว่า ซึ่งทำให้เรารู้ว่าการกระจายตัวแบบใดมีค่าที่กระจายมากกว่า
3. ความไม่สมมาตรเปรียบเทียบกันอย่างไร?
หากฮิสโตแกรมมี “ส่วนท้าย” ทางด้านซ้ายของโครงเรื่อง แสดงว่ามีการบิดเบือนในเชิงลบ ในทางกลับกัน หากฮิสโตแกรมมี “ส่วนท้าย” อยู่ทางด้านขวาของโครงเรื่อง ก็ถือว่ามีการเบี่ยงเบนไปในทางบวก เราสามารถตรวจสอบฮิสโตแกรมแต่ละอันด้วยสายตาเพื่อเปรียบเทียบ ความเบ้
ตัวอย่างต่อไปนี้แสดงวิธีเปรียบเทียบฮิสโตแกรมสองอันที่แตกต่างกันและตอบคำถามสามข้อนี้
ตัวอย่าง: การเปรียบเทียบฮิสโตแกรม
สมมติว่านักเรียน 200 คนใช้วิธีการเรียนวิธีหนึ่งเพื่อเตรียมตัวสำหรับการสอบ และนักเรียนอีก 200 คนใช้วิธีการเรียนที่แตกต่างกันเพื่อเตรียมตัวสำหรับการสอบเดียวกัน
สมมติว่าเราสร้างฮิสโตแกรมต่อไปนี้เพื่อเปรียบเทียบผลการสอบของนักเรียนแต่ละกลุ่ม:
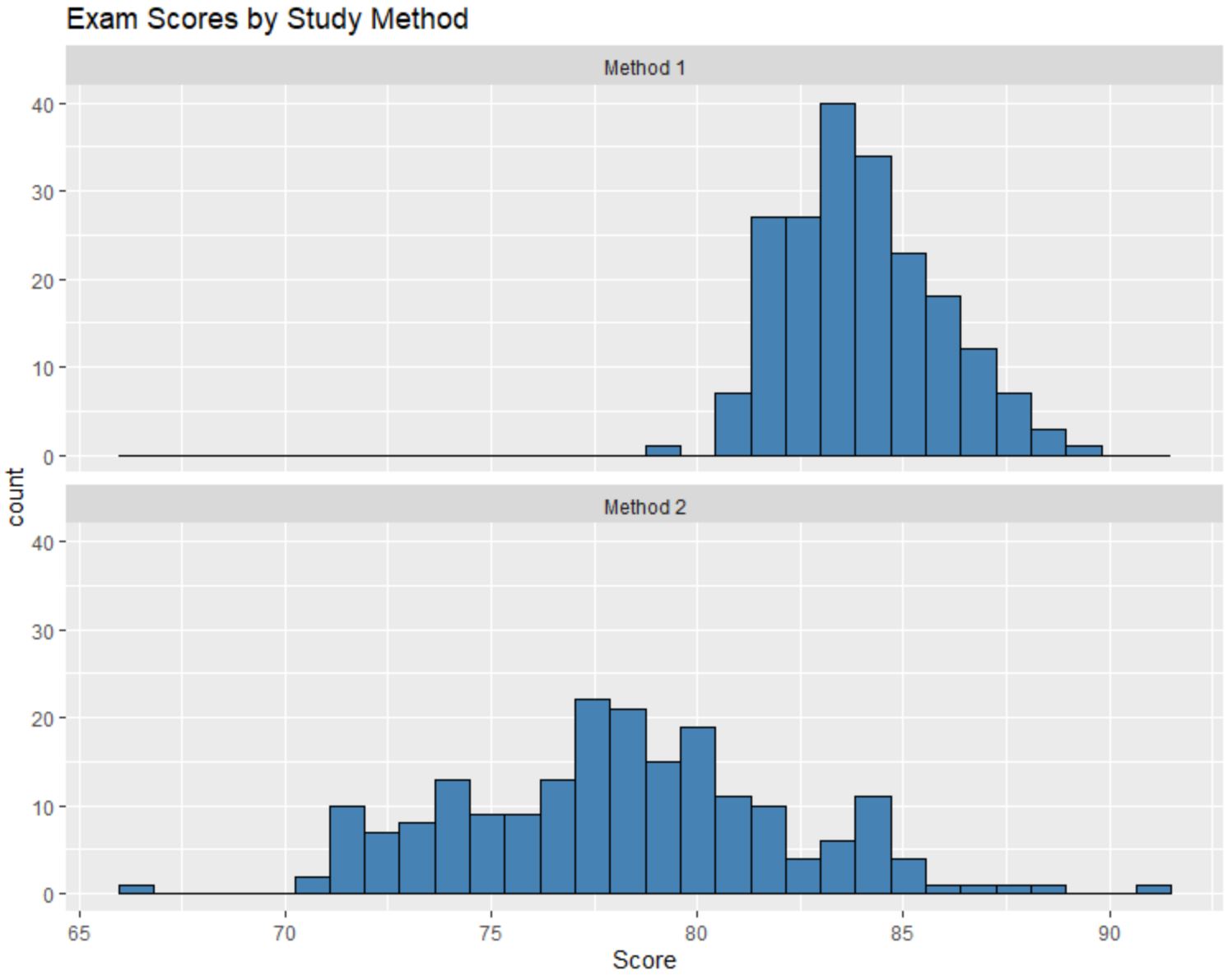
เราสามารถเปรียบเทียบฮิสโตแกรมเหล่านี้และตอบคำถามสามข้อต่อไปนี้:
1. ค่ามัธยฐานเปรียบเทียบกันอย่างไร?
แม้ว่าเราจะไม่ทราบค่ามัธยฐานที่แน่นอนของการแจกแจงแต่ละครั้งเพียงแค่ดูฮิสโตแกรม แต่ก็ชัดเจนว่าคะแนนสอบมัธยฐานของนักเรียนที่ใช้วิธีที่ 1 นั้นสูงกว่าคะแนนสอบมัธยฐานของนักเรียนที่ใช้วิธีที่ 1 ที่ใช้ วิธีที่ 2 .
เราสามารถประมาณได้ว่าค่ามัธยฐานของวิธีที่ 1 อยู่ที่ประมาณ 84 และค่ามัธยฐานของวิธีที่ 2 อยู่ที่ประมาณ 78
2. การกระจายตัวเปรียบเทียบกันอย่างไร?
ค่าฮิสโตแกรมสำหรับวิธีที่ 2 นั้นกระจัดกระจายมากกว่าค่าของวิธีที่ 1 ซึ่งบอกเราว่าผลการสอบสำหรับนักเรียนที่ใช้วิธีที่ 2 มีการกระจายตัวมากกว่ามาก
3. ความไม่สมมาตรเปรียบเทียบกันอย่างไร?
เมื่อดูฮิสโตแกรม ปรากฏว่าการกระจายของคะแนนการทดสอบสำหรับวิธีที่ 1 เอียงไปทางขวาเล็กน้อย ตามที่ระบุโดย “ส่วนท้าย” ที่ขยายไปทางขวาของฮิสโตแกรม
อย่างไรก็ตาม ปรากฏว่าไม่มี “หาง” ในการกระจายผลการสอบสำหรับวิธีที่ 2 ซึ่งบอกเราว่าการกระจายน้อยหรือไม่เบ้
โบนัส : นี่คือโค้ดที่เราใช้ใน R เพื่อสร้างฮิสโตแกรมทั้งสองนี้:
library (ggplot2)
#make this example reproducible
set. seeds (0)
#create data frame
df <- data. frame (method=rep(c(' Method 1 ', ' Method 2 '), each= 200 ),
Score=c(rnorm( 200 , mean= 84 , sd= 2 ),
rnorm( 200 , mean= 78 , sd= 4 )))
#create histogram of scores for each method
ggplot(df, aes(x=Score)) +
geom_histogram(fill=' steelblue ', color=' black ') +
facet_wrap(.~method, nrow= 2 ) +
labs(title=' Exam Scores by Study Method ')
แหล่งข้อมูลเพิ่มเติม
บทช่วยสอนต่อไปนี้จะอธิบายวิธีทำงานทั่วไปอื่นๆ ด้วยฮิสโตแกรม:
วิธีประมาณค่าเฉลี่ยและค่ามัธยฐานของฮิสโตแกรมใดๆ
วิธีประมาณค่าเบี่ยงเบนมาตรฐานของฮิสโตแกรมใดๆ
วิธีอธิบายรูปร่างของฮิสโตแกรม