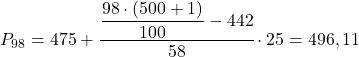เปอร์เซ็นต์ไทล์ (สถิติ)

โดย ดร.เบนจามิน แอนเดอร์สัน สิงหาคม 5, 2023 สถิติ 0 ความคิดเห็น

บทความนี้จะอธิบายว่าเปอร์เซ็นไทล์คืออะไรและมีการคำนวณอย่างไร คุณจะพบกับแบบฝึกหัดเปอร์เซ็นไทล์ที่แก้ได้ และนอกจากนี้ คุณจะสามารถคำนวณเปอร์เซ็นไทล์ใดๆ ของตัวอย่างข้อมูลของคุณด้วยเครื่องคิดเลขออนไลน์ได้

เปอร์เซ็นไทล์คืออะไร?

ในทางสถิติ เปอร์เซ็นไทล์คือค่าที่แบ่งชุดข้อมูลที่เรียงลำดับออกเป็นหนึ่งร้อยส่วนเท่าๆ กัน ดังนั้น เปอร์เซ็นไทล์จะระบุค่าที่ต่ำกว่าซึ่งเปอร์เซ็นต์ของชุดข้อมูลอยู่

ตัวอย่างเช่น ค่าเปอร์เซ็นไทล์ที่ 35 สูงกว่า 35% ของข้อมูลที่สังเกตได้ แต่ต่ำกว่าข้อมูลที่เหลือ

เปอร์เซ็นต์จะแสดงด้วยอักษรตัวใหญ่ P และดัชนีเปอร์เซ็นไทล์ กล่าวคือ เปอร์เซ็นไทล์ที่ ₁ คือ P 1 เปอร์เซ็นไทล์ที่ 40 คือ P ₄₀ เปอร์เซ็นไทล์ที่ 79 คือ P ₇₉ และอื่นๆ

👉 คุณสามารถใช้เครื่องคิดเลขด้านล่างเพื่อคำนวณเปอร์เซ็นไทล์ของชุดข้อมูลใดก็ได้

ในทำนองเดียวกัน เปอร์เซ็นต์ไทล์เป็นหน่วยวัดตำแหน่งที่ไม่อยู่ตรงกลาง ร่วมกับควอร์ไทล์ ควินไทล์ และเดซิล คุณสามารถตรวจสอบความหมายของควอนไทล์แต่ละประเภทได้จากเว็บไซต์ของเรา

ควรสังเกตว่าคำว่าเปอร์เซ็นไทล์ยังใช้เพื่อเปรียบเทียบน้ำหนักและส่วนสูงของทารกกับค่ามาตรฐานของทารกคนอื่น ๆ เนื่องจากมีตารางการเติบโตพร้อมค่าที่บันทึกไว้ซึ่งช่วยพิจารณาว่าทารกเติบโตอย่างถูกต้องหรือไม่ . .

วิธีการคำนวณเปอร์เซ็นไทล์

ใน การคำนวณตำแหน่งของเปอร์เซ็นไทล์ ของชุดข้อมูลทางสถิติ คุณต้องคูณจำนวนเปอร์เซ็นไทล์ด้วยผลรวมของจำนวนจุดข้อมูลทั้งหมดบวกหนึ่ง แล้วหารผลลัพธ์ด้วยหนึ่งร้อย

สูตรเปอร์เซ็นไทล์ จึงเป็นดังนี้:

$\cfrac{k\cdot (n+1)}{100} \qquad k=1, 2, 3,\ldots ,97,98,99$

โปรดทราบ: สูตรนี้บอกเราถึงตำแหน่งของเปอร์เซ็นไทล์ แต่ไม่ใช่ค่าของมัน เปอร์เซ็นไทล์จะเป็นข้อมูลที่อยู่ในตำแหน่งที่ได้จากสูตร

อย่างไรก็ตาม บางครั้งผลลัพธ์ของสูตรนี้จะให้ค่าเป็นเลขทศนิยม ดังนั้น เราจึงต้องแยกความแตกต่างออกเป็น 2 กรณี ขึ้นอยู่กับว่าผลลัพธ์เป็นเลขทศนิยมหรือไม่:

หากผลลัพธ์ของสูตรเป็น ตัวเลขที่ไม่มีส่วนทศนิยม เปอร์เซ็นไทล์จะสอดคล้องกับข้อมูลที่อยู่ในตำแหน่งที่ระบุในสูตรด้านบน
หากผลลัพธ์ของสูตรเป็น ตัวเลขที่มีส่วนทศนิยม ค่าเปอร์เซ็นไทล์ที่แน่นอนจะคำนวณโดยใช้สูตรต่อไปนี้:

$P=x_i+d\cdot (x_{i+1}-x_i)$

โดยที่ x _i และ x _i+1 คือตัวเลขของตำแหน่งระหว่างตำแหน่งที่มีตัวเลขที่ได้จากสูตรแรกอยู่ และ d คือส่วนทศนิยมของตัวเลขที่ได้จากสูตรแรก

ตอนนี้คุณอาจคิดว่าการค้นหาเปอร์เซ็นไทล์ของกลุ่มตัวอย่างหรือประชากรทางสถิตินั้นซับซ้อนเพราะวิธีการนี้มีหลายขั้นตอน แต่จริงๆ แล้วง่ายมาก อ่านตัวอย่างที่เป็นรูปธรรมสองตัวอย่างต่อไปนี้ และฉันมั่นใจว่าคุณจะเข้าใจดีขึ้นมาก

หมายเหตุ : ชุมชนวิทยาศาสตร์ยังไม่มีข้อตกลงที่สมบูรณ์เกี่ยวกับวิธีคำนวณเปอร์เซ็นไทล์ ดังนั้นคุณจึงสามารถหาหนังสือสถิติที่อธิบายแตกต่างออกไปเล็กน้อยได้

ตัวอย่างการคำนวณเปอร์เซ็นต์

ดังที่คุณเห็นข้างต้นในการอธิบายวิธีหาเปอร์เซ็นต์ไทล์ของกลุ่มตัวอย่าง การคำนวณจะแตกต่างกันไปขึ้นอยู่กับว่าผลลัพธ์ของสูตรแรกเป็นทศนิยมหรือไม่ นั่นเป็นเหตุผลที่ด้านล่างนี้คุณจะพบตัวอย่างที่แก้ไขแล้วสองตัวอย่าง หนึ่งตัวอย่างสำหรับแต่ละกรณี

ตัวอย่างที่ 1

จากข้อมูลที่แสดงในตารางต่อไปนี้ ให้คำนวณเปอร์เซ็นไทล์ที่ 1, 43 และ 89

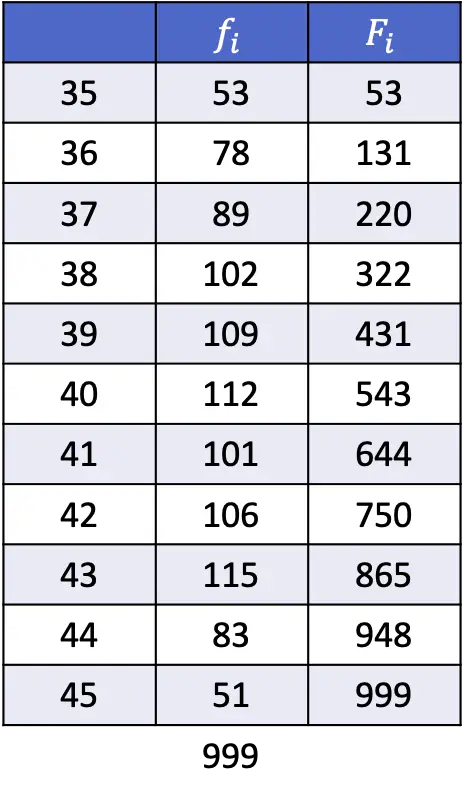
ตามที่อธิบายไว้ในส่วนที่แล้ว สูตรในการค้นหาตำแหน่งของเปอร์เซ็นไทล์คือ:

$\cfrac{k\cdot (n+1)}{100} \qquad k=1, 2, 3,\ldots ,97,98,99$

ในกรณีนี้ ขนาดของกลุ่มตัวอย่างสำหรับแบบฝึกหัดนี้คือข้อมูลทางสถิติ 999 รายการ ดังนั้นในการคำนวณตำแหน่งของเปอร์เซ็นไทล์แรก เราจำเป็นต้องแทนที่ 999 สำหรับ n และ 1 ด้วย k :

$\cfrac{1\cdot (999+1)}{100}=10\quad \color{orange}\bm{\longrightarrow}\color{black}\quad P_1=35$

ดังนั้นเปอร์เซ็นไทล์ที่ 1 จะเป็นค่าที่มีความถี่สัมบูรณ์สะสมมากกว่า 10 ทันที ซึ่งในกรณีนี้คือ 35 เนื่องจากมีความถี่สัมบูรณ์สะสมเป็น 53

ในการหาเปอร์เซ็นไทล์ที่ 43 คุณต้องใช้สูตรเดียวกัน แต่คราวนี้เราแทนที่ k ด้วย 43

$\cfrac{43\cdot (999+1)}{100}=430\quad \color{orange}\bm{\longrightarrow}\color{black}\quad P_{43}=39$

ความถี่สะสมสัมบูรณ์ที่อยู่เหนือ 430 ทันทีคือ 431 ของข้อมูล 39 ดังนั้นเปอร์เซ็นไทล์ที่ 43 จึงเท่ากับ 39

สุดท้าย เราใช้สูตรเดียวกันเพื่อให้ได้เปอร์เซ็นไทล์ที่ 89:

$\cfrac{89\cdot (999+1)}{100}=890\quad \color{orange}\bm{\longrightarrow}\color{black}\quad P_{89}=44$

ความถี่สัมบูรณ์สะสมของค่า 44 คือ 948 ซึ่งมากกว่า 890 ทันที ดังนั้น เปอร์เซ็นต์ไทล์ที่ 89 คือ 44

ตัวอย่างที่ 2

ค้นหาเปอร์เซ็นไทล์ที่ 35 และ 67 ของชุดข้อมูลต่อไปนี้:

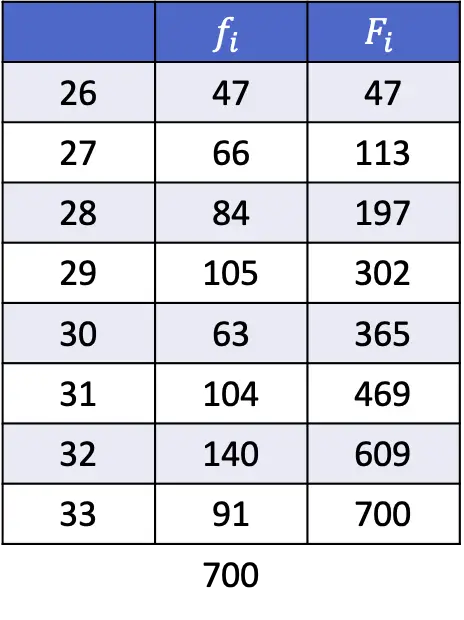
แม้ว่าในแบบฝึกหัดนี้เราจะต้องคำนวณเพิ่มเติม แต่หลักการยังคงเหมือนเดิม: เราต้องคำนวณตำแหน่งเปอร์เซ็นไทล์ด้วยนิพจน์ต่อไปนี้

$\cfrac{k\cdot (n+1)}{10} \qquad k=1, 2, 3,\ldots ,97,98,99$

ดังนั้น ในการคำนวณเปอร์เซ็นไทล์ที่ 35 เราจึงแทนที่ k ด้วย 35 และ n ด้วยจำนวนข้อมูลทั้งหมด เช่น 700:

$\cfrac{35\cdot (700+1)}{100}=245,35$

แต่คราวนี้เราได้เลขทศนิยมจากสูตร ดังนั้น เราจำเป็นต้องใช้นิพจน์พีชคณิตต่อไปนี้เพื่อคำนวณค่าเปอร์เซ็นไทล์ที่แน่นอน:

$P=x_i+d\cdot (x_{i+1}-x_i)$

ตัวเลขที่กำหนดโดยสูตรแรกคือ 245.35 ดังนั้นเปอร์เซ็นไทล์ที่ 35 จึงอยู่ระหว่างตำแหน่ง 245 และ 246 ซึ่งสอดคล้องกับค่า 29 และ 29 ตามลำดับ ดังนั้น x _i คือ 29 x _i+1 คือ 29 และ d มีค่าเท่ากับส่วนทศนิยมของตัวเลขที่ได้รับ เช่น 0.35

$P_{35}=29+0,35\cdot (29-29)=29$

หากต้องการหาเปอร์เซ็นไทล์ที่ 67 เราจำเป็นต้องใช้วิธีเดียวกัน ขั้นแรกเราคำนวณตำแหน่งเปอร์เซ็นไทล์:

$\cfrac{67\cdot (700+1)}{100}=469,67$

ผลลัพธ์ที่ได้คือ 469.67 ระบุว่าเปอร์เซ็นไทล์จะอยู่ระหว่างตำแหน่ง 469 ถึง 470 ซึ่งค่าคือ 31 และ 32 ดังนั้นเราจึงใช้สูตรที่สองในกระบวนการค้นหาค่าเปอร์เซ็นไทล์ที่แน่นอน:

$P_{67}=31+0,67\cdot (32-31)=31,67$

เครื่องคิดเลขเปอร์เซ็นไทล์

ป้อนชุดข้อมูลทางสถิติและจำนวนเปอร์เซ็นไทล์ที่คุณต้องการคำนวณลงในเครื่องคิดเลขต่อไปนี้ ข้อมูลต้องคั่นด้วยช่องว่างและป้อนโดยใช้จุดเป็นตัวคั่นทศนิยม

เปอร์เซ็นต์ไทล์ในข้อมูลที่จัดกลุ่ม

ใน การคำนวณเปอร์เซ็นไทล์เมื่อข้อมูลถูกจัดกลุ่มเป็นกลุ่ม ก่อนอื่นเราต้องค้นหากลุ่มหรือคลาสที่มีเปอร์เซ็นไทล์อยู่โดยใช้สูตรต่อไปนี้:

$\cfrac{k\cdot (n+1)}{100} \qquad k=1, 2, 3,\ldots ,97,98,99$

ดังนั้นเปอร์เซ็นไทล์จึงอยู่ในช่วงเวลาที่ความถี่สัมบูรณ์มากกว่าจำนวนที่ได้รับในนิพจน์ก่อนหน้าทันที

และเมื่อเราทราบช่วงที่เป็นเปอร์เซ็นไทล์แล้ว เราต้องใช้สูตรต่อไปนี้เพื่อค้นหาค่าที่แน่นอนของเปอร์เซ็นไทล์:

$P_k=L_i+\cfrac{\displaystyle\frac{k\cdot (n+1)}{100}-F_{i-1}}{f_i}\cdot I_i \qquad k=1,2,3,\ldots ,97,98,99$

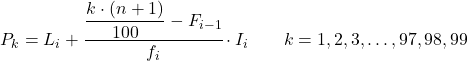
ทอง:

L _i คือขีดจำกัดล่างของช่วงเวลาที่เปอร์เซ็นไทล์อยู่
n คือจำนวนการสังเกตทั้งหมด
F _i-1 คือความถี่สัมบูรณ์สะสมของช่วงก่อนหน้า
f _i คือความถี่สัมบูรณ์ของช่วงเวลาที่เปอร์เซ็นไทล์อยู่
_ฉัน คือความกว้างของช่วงเปอร์เซ็นไทล์

ด้านล่างนี้คือแบบฝึกหัดทีละขั้นตอนเกี่ยวกับวิธีรับเปอร์เซ็นไทล์เมื่อข้อมูลแสดงเป็นช่วงๆ โดยเฉพาะจะมีการคำนวณเปอร์เซ็นไทล์ที่ 29, 52 และ 98

ข้อมูลในตัวอย่างนี้ถูกจัดกลุ่มเป็นช่วงเวลา ดังนั้นเราจึงต้องทำสองขั้นตอนในการกำหนดเปอร์เซ็นไทล์ ขั้นแรกเราต้องค้นหาช่วงเวลาที่เปอร์เซ็นไทล์อยู่ จากนั้นจึงใช้สูตรเพื่อคำนวณค่าที่แน่นอนของเปอร์เซ็นไทล์ เปอร์เซ็นไทล์

ดังนั้นเราจึงพบตำแหน่งของเปอร์เซ็นไทล์ที่ 29 ด้วยนิพจน์ต่อไปนี้:

$\cfrac{k\cdot (n+1)}{100}$

$\cfrac{29\cdot (500+1)}{100} =145,29 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [350,375)$

ช่วงเปอร์เซ็นไทล์จะเป็นช่วงที่มีความถี่สัมบูรณ์สะสมมากกว่า 145.29 ทันที ซึ่งในกรณีนี้คือช่วง [350.375) ซึ่งมีความถี่สัมบูรณ์สะสมคือ 175 และเมื่อเราทราบช่วงเปอร์เซ็นไทล์แล้ว เราจะใช้สูตรต่อไปนี้เพื่อคำนวณ ค่าที่แน่นอน:

$P_k=L_i+\cfrac{\displaystyle\frac{k\cdot (n+1)}{100}-F_{i-1}}{f_i}\cdot I_i$

$P_{29}=350+\cfrac{\displaystyle\frac{29\cdot (500+1)}{100}-131}{44}\cdot 25=358,12$

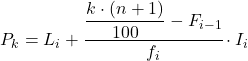
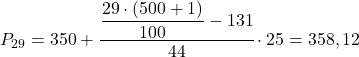
ตอนนี้เราทำซ้ำขั้นตอนเดียวกันเพื่อคำนวณเปอร์เซ็นไทล์ที่ 52 ก่อนอื่นเราคำนวณช่วงเวลา:

$\cfrac{52\cdot (500+1)}{100} =260,52 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [400,425)$

ช่วงเปอร์เซ็นไทล์ที่ 52 คือ [400.425) เนื่องจากความถี่สัมบูรณ์สะสม (298) เป็นความถี่ที่สูงกว่า 260.52 ทันที ดังนั้นค่าเปอร์เซ็นไทล์ที่แน่นอนจะเป็นดังนี้:

$P_{52}=400+\cfrac{\displaystyle\frac{52\cdot (500+1)}{100}-234}{64}\cdot 25=410,36$

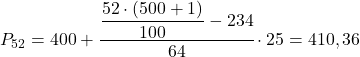
สุดท้ายเราจะพบเปอร์เซ็นไทล์ที่ 98 และเช่นเคย เราจะคำนวณช่วงเวลาที่มันอยู่ก่อน:

$\cfrac{98\cdot (500+1)}{100} =490,98 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [475,500)$

และเมื่อเราทราบช่วงที่เปอร์เซ็นไทล์อยู่ เราจะคำนวณค่าที่แน่นอนด้วยสูตรต่อไปนี้:

$P_{98}=475+\cfrac{\displaystyle\frac{98\cdot (500+1)}{100}-442}{58}\cdot 25=496,11$

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

สวัสดี ฉันชื่อเบนจามิน ศาสตราจารย์สถิติเกษียณอายุแล้ว และผันตัวมาเป็นครูสอนสถิติโดยเฉพาะ ด้วยประสบการณ์และความเชี่ยวชาญที่กว้างขวางในสาขาสถิติ ฉันกระตือรือร้นที่จะแบ่งปันความรู้ของฉันเพื่อเสริมศักยภาพนักเรียนผ่าน Statorials. รู้เพิ่มเติม

เปอร์เซ็นไทล์คืออะไร?

วิธีการคำนวณเปอร์เซ็นไทล์

ตัวอย่างการคำนวณเปอร์เซ็นต์

ตัวอย่างที่ 1

ตัวอย่างที่ 2

เครื่องคิดเลขเปอร์เซ็นไทล์

เปอร์เซ็นต์ไทล์ในข้อมูลที่จัดกลุ่ม

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

เพิ่มความคิดเห็น